Алгоритмы трассировки проводных соединений

В современных радиоэлектронных средствах трассировку проводных соединений выполняют обычно одним из трех способов: по прямым, соединяющим контакты отдельных компонентов (монтаж в навал), жгутовым монтажом, монтажом по каналам. В первом случае получаются максимальная простота конструктивной реализации межсоединений, высокая помехоустойчивость, минимальные задержки сигналов в проводниках. К недостаткам монтажа в навал следует отнести трудности контроля и при высокой плотности плохую ремонтопригодность.

Второй способ предполагает объединение отдельных проводников в жгуты. Этот способ более технологичен, прост в контроле, однако обладает малой помехоустойчивостью из-за больших параллельных участков у рядом расположенных проводников и, как следствие, больших связей между ними.

В дальнейшем ограничимся только рассмотрением особенностей построения алгоритмов для трассировки проводного монтажа в навал. Задачу трассировки такого монтажа можно сформулировать следующим образом [8]: задана графовая модель устройства МУ4 координатами множества контактов C и сигнальными ветвями W. Необходимо построить в графе G(E, C, B, W) дерево, включающее все контактные вершины графа C и имеющее минимальную суммарную длину сигнальных ветвей.

Именно такие варианты соединения контактов отдельных компонентов рациональны, так как обеспечивают минимальные задержки сигналов в проводниках и отсутствие вихревых токов. Иногда задача построения таких деревьев называется задачей построения кратчайших связывающих сетей.

Известно много алгоритмов построения кратчайших связывающих сетей, из которых рассмотрим только алгоритм Прима.

Этот алгоритм позволяет строить кратчайшие связывающие сети при наличии ограничений на степени вершин дерева, т.е. количества проводников, подключенных к одному контакту.

Построение дерева алгоритмом Прима выполняется в несколько этапов. На первом из них выделяется подмножество вершин C_i подграфа G'_i, которые должны быть соединены эквипотенциальной цепью. Далее любая произвольная вершина трассируемого подмножества соединяется с ближайшей соседней цепью, образуя исходное поддерево G'_i подграфа. На каждом последующем шаге к строящемуся поддереву присоединяют очередную ветвь минимально возможной длины, связывающую новую, еще не подключенную вершину c_kÎC_i с одной из вершин поддерева G', локальная степень которой меньше допустимой. Для реализации алгоритма составляется матрица длин D, строки и столбцы которой соответствуют множеству контактов устройства, соединения между которыми трассируются, а элементы равны расстоянию между контактами, если эти контакты должны быть соединены электрической цепью, и равны нулю в противоположном случае. Для удобства программной реализации алгоритма в матрице длин D контакты, относящиеся к одной электрической цепи, располагаются друг за другом, образуя в D ненулевые диагональные подматрицы и нулевые внедиагональные. Так, для МКП с контактами, схематически показано на рис. 7.3, а, матрица длин будет иметь следующий вид:

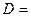
		c1	c2	c6	c3	c4	s5	.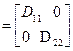
c1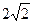
c2
c6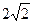
c3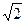
c4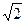
c5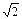

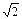
а) б)

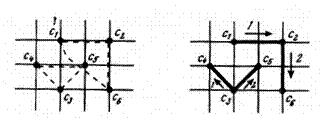
Рис. 7.3. Трассировка проводного монтажа: а – группы эквивалентных контактов, б – построение кратчайших связывающих сетей алгоритмом Прима

При трассировке первой электрической цепи в любой строке первой подматрицы D₁₁, например первой, выбирают контакт c₁ и, просматривая строку, находят ближайший к нему контакт этого же электрического соединения. В нашем случае это будет контакт c₂. Контакты c₁ и c₂ соединяют, а первый и второй столбцы матрицы исключают из дальнейшего рассмотрения. Далее, просматривая первую и вторую строки матрицы D₁₁, находят контакт, находящийся на минимальном расстоянии от уже соединенных трассой c₁ и c₂, это будет c₆. Если расстояние от c₂ до c₆ меньше, чем между c₁ и с₆, то соединяются контакты c₂ и с₆ и третий столбец D также исключают из дальнейшего рассмотрения. Далее пересматриваются строки, соответствующие первому, второму и шестому контактам, находится наиболее близкий к ним следующий контакт, и так продолжается до окончания трассировки всего соединения. После завершения трассировки первой цепи переходят к трассировке второй, задаваемой подматрицей длин D₂₂, и т.д. Порядок трассировки соединений для примера на рис. 7.3, а показан на рис. 7.3, б.

Кроме того, на каждом шаге алгоритма можно проверять локальную степень вершины, от которой должен проходить проводник, и если она превышает заданную величину (число проводников, которое может быть присоединено к контакту, превышает допустимое), то соединение осуществляют с другой вершиной, расположенной наиболее близко к выбранному контакту. Если в матрице длин D для отдельных соединений вводить дополнительные весовые функции, то можно с помощью описанного алгоритма реализовать и другие критерии трассировки.

Алгоритм 7.8. Алгоритм построения кратчайшего дерева проводного монтажа (Прима)

Шаг 1. Упорядочивается расположение контактов в соответствии с электрическими соединениями, формируется матрица длин D.

Шаг 2. Выбираются трассируемое электрическое соединение и контакт c_j, от которого начинается трассировка. Контакт c_j заносится во множество соединенных данной цепью контактов C_i.

Шаг 3. По матрице длин выбирается контакт, находящийся на минимальном расстоянии от уже соединенных контактов из множества C_i. Осуществляется соединение контакта c_j с ближайшим ему контактом из множества C_i, если степень вершины контакта меньше заданной.

Шаг 4. Столбец и строки матрицы длин D, соответствующие контакту c_j, исключаются из матрицы.

Шаг 5. Если не все контакты цепи соединены, то переход к шагу 5.

Шаг 6. Если не все электрические соединения протрассированы, то переход к шагу 2.

Шаг 7. В соответствии с полученными результатами разрабатыватеся управляющая программа для автомата трассировки проводного монтажа в МКП.

Известны и другие алгоритмы построения кратчайших связующих сетей, предложенные в работах Краскалла, Лобермана, Уйэнберга.