Типовые задачи конструкторского проектирования РЭС и алгоритмы их решения . Алгоритмы компоновки конструктивных модулей
При проектировании РЭС задача компоновки решается на различных иерархических уровнях: компоновка модулей или интегральных схем из логических элементов, компоновка плат из микросхем и т.д. В общем случае компоновка представляет собой процесс составления конструктивных модулей i-го уровня из модулей (i–1)-го уровня в соответствии с заданными критериями, ограничениями и схемой соединения модулей (i–1)-го уровня: функциональной (ФС) либо принципиальной электрической (ПЭС). В зависимости от принятых критериев существует три варианта постановки задач компоновки [8,9]:
– типизация – разбиение ФС (или ПЭС) на части по критерию минимума числа разнотипных узлов (минимум номенклатуры узлов);
– покрытие – преобразование ФС в ПЭС, т.е. в схему соединения конструктивных модулей, номенклатура которых заранее известна;
– разрезание – разбиение ФС (или ПЭС) на части, соответствующие модулям более высокого уровня, с минимизацией числа связей между этими частями, причем число частей может задаваться или определяться в процессе решения.
Наиболее часто разработчику радиоэлектронных средств приходится решать задачи покрытия и разрезания, поэтому рассмотрим их более подробно.
Исходными данными для решения задачи покрытия являются функциональная схема устройства и схемы типовых конструктивных модулей, с помощью которых должно быть реализовано устройство. Задачей покрытия является распределение фрагментов функциональной схемы устройства по отдельным конструктивным компонентам более низкого уровня, например логических элементов по корпусам микросхем из заданного набора, при котором обеспечивается оптимум какого-либо качества: минимум числа модулей, реализующих функциональную схему устройства; минимум межмодульных соединений и т.п.
Функциональная схема устройства представляется графовыми моделями VG(S, V) – МУ1 или MG(S, V) – МУ2, множество решений которых S интерпретирует логические элементы, а множество ветвей V – связи между ними. Каждый конструктивный модуль, с помощью которых будет реализовываться устройство (интегральную микросхему), можно представить в виде подграфа G′i. В результате получим количество подграфов, соответствующее числу типов модулей, выбранных для покрытия схемы устройства. Это позволяет математически сформулировать задачу покрытия функциональной схемы заданным набором конструктивных модулей как задачу покрытия графа VG или MG подграфами из множества G′i…G′k, исходя из критерия минимума подграфов G′i, либо связей между ними. Если вершины графа MG помечены метками, характеризующими тип логического элемента, или интерпретируемого, как это делается в разновидности модели МУ2, то каждой ветви графа, соединяющей конструктивные модули, можно поставить в соответствие функцию веса:
æ1, если ветвь vij инцидентна однотипным
pij= í вершинам si и sj
è0, если инцидентые вершины si и sj не однотипны
Поскольку внутри модуля (интегральной микросхемы) обычно объединяются однотипные компоненты, критерием для оптимального решения задачи покрытия графа MG подграфами из множества G′ является
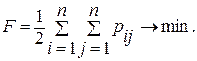
Однако прямое решение сформулированной выше задачи наталкивается на значительные вычислительные и алгоритмические трудности.
Поэтому решение задачи покрытия обычно выполняют в два этапа. На первом этапе решается предельная задача, которая позволяет определить оптимальные числа модулей каждого типа, используемых для решения задачи покрытия, но при этом не определяется, в какой конструктивный модуль будут входить те или иные функциональные элементы. На втором этапе происходит собственно распределение функциональных элементов по конструктивным модулям, критерием оптимальности которого служит решение, полученное на предыдущем этапе.
Предельная задача покрытия в большинстве случаев может быть сведена к задаче линейного программирования.
Задача линейного программирования может решать в непрерывном пространстве с округлением полученных в результате решения оптимальных значений переменных (количеств конструктивных модулей) до ближайшего целочисленного значения, чем создается некоторая избыточность покрытия, обычно всегда предусматриваемая в реальных устройствах. Если же в избыточности нет необходимости, то задача может быть решена одним из методов решения целочисленной задачи линейного программирования, например методом ветвей и границ.
На втором этапе решения задачи покрытия обычно используют быстрые эвристические алгоритмы, с помощью которых после многократного прогона задачи удается получить покрытие функциональной схемы, близкое к предельному решению. Суть подавляющего большинства этих алгоритмов состоит в выделении из функциональной схемы устройства групп логических элементов, максимально связанных между собой, и дальнейшей проверке на совпадение логических функций выделенной группы элементов с логическими функциями конструктивных модулей из заданного набора. Группа логических элементов закрепляется за тем конструктивным модулем, в состав которого входит наибольшее число содержащихся в ней логических элементов. Оставшиеся элементы покрываются на следующем шаге или вручную.
Этот процесс повторяется для большого числа вариантов выделенных из функциональной схемы устройства групп логических элементов, пока не будет получен результат, близкий к предельному.
Алгоритм 7.1. Покрытия функциональной схемы заданным набором конструктивных модулей
Шаг 1. Из функциональной схемы устройства выделяется множество непокрытых логических элементов.
Шаг 2. Выбирается один из непокрытых элементов, имеющий максимальное число связей с остальными. Формируется группа из логических элементов, имеющих наибольшее число связей с выделенным.
Шаг 3. Производится позиционное сравнение логических функций, содержащихся в конструктивных модулях из заданного набора и группе выделенных элементов.
Шаг 4. Группа выделенных логических элементов закрепляется за конструктивным модулем, если совпали логические функции в модуле и группе выделенных элементов, иначе наименее связанный элемент исключается из группы, и переход к шагу 3.
Шаг 5. Проверяется множество непокрытых элементов; если оно не пустое, то переход к шагу 2.
Шаг 6. Проверяется близость покрытия к предельному. Если полученное покрытие удовлетворяет по своим характеристикам, то переход к формированию ПЭС, иначе переход к шагу 1.
Рассмотрим алгоритм решения задачи разрезания. Для ее решения разработано большое число алгоритмов, отличающихся друг от друга структурой, объемом, используемыми критериями оптимальности. В качестве критерия оптимальности компоновки обычно используют следующие: каждый из конструктивных модулей более высокого уровня должен содержать не более N компонентов низкого уровня и R выводов; минимум числа соединений между модулями; минимум числа модулей и т.д. В связи с тем, что многие критерии противоречивы, задача компоновки оказывается трудноразрешимой, и существующие алгоритмы удовлетворяют лишь нескольким из перечисленных условий.
Для решения задачи разрезания обычно используется модель устройства МУ1 в виде взвешенного графа VG(S, V).
В терминах теории графов основная задача компоновки – задача разрезания – может быть сформулирована как задача разбиения графа VG(S, V) (описывающего модули высшего уровня) на подграфы G′ следующим образом:
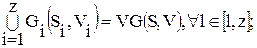
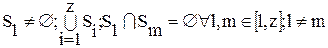
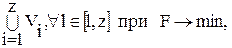
где Sl, Vl – множество вершин и цепей, принадлежащих подграфу Gl, соотвествующему модулю низшего уровня; z – число подграфов Gl, на которые разбивается ВГС VG(S, V) (число модулей низшего уровня в модуле высшего уровня); F – критерий качества компоновки, который, например, при минимизации числа соединений между модулями будет определять как
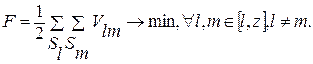
Эти условия означают, что в каждом подграфе разбиения должна быть хотя бы одна вершина, объединение всех вершин подграфов Gl составит множество вершин графа S, никакая из вершин si не может входить одновременно в два (или более) подграфов Gl, объединение всех ветвей uij подграфа Vl составит полное множество ветвей графа VG – V.
Все существующие алгоритмы разрезания можно условно разделить на следующие классы: последовательные алгоритмы; итерационные алгоритмы; алгоритмы назначения; смешанные алгоритмы. В существующих САПР наиболее часто используются последовательные и итерационные алгоритмы.
В этих алгоритмах в качестве критерия качества компоновки наиболее удобно использовать критерий минимума числа связей между отдельными подграфами, соответствующими конструктивным модулям нижнего уровня.
Для пояснения существа работы последовательного и итерационного алгоритмов определим число связей между двумя подграфами Gl и Gm (Gl, Gm ÎVG) через элементы матрицы смежностей qij:
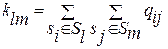 , (7.1)
, (7.1)
где Sl и Sm – все вершины, принадлежащие подграфам Gl и Gm соответственно.
Общее число связей между подграфами разбиения
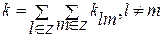 , (7.2)
, (7.2)
где z – множество номеров подграфов Gl.
Выражения (7.1) и (7.2) имеют ясный физический смысл и поясняются рис. 7.1, а, б, где показаны два варианта разрезания устройства, заданного взвешенным графом VG(S, V), на подграфы G1 и G2. В матрице смежностей Q, описывающей граф VG, вершины расположены следующим образом: вначале перечислим вершины, относящиеся к подграфу G1 (s1, s2, s3 для первого варианта разрезаний и s1, s4, s5 для второго варианта), а затем вершины, относящиеся ко второму подграфу G2. Варианты записей матрицы смежностей при принятом порядке перечисления вершин графа для двух вариантов разрезания приведены ниже:
| s1 | s2 | s3 | s4 | s5 | s6 | |||||
| s1 | ||||||||||
| s2 | ||||||||||
| Q’= | s3 | = | Q’11 | Q’12 | ||||||
| s4 | Q’21 | Q’22 | ||||||||
| s5 | ||||||||||
| s6 |
| s1 | s2 | s3 | s4 | s5 | s6 | |||||
| s1 | ||||||||||
| s2 | ||||||||||
| Q”= | s3 | = | Q”11 | Q”12 | ||||||
| s4 | Q”21 | Q”22 | ||||||||
| s5 | ||||||||||
| s6 |
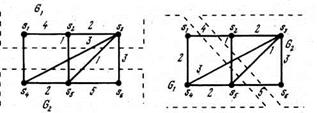 |
а) б)
Рис. 7.1. Различные варианты разрезания графа на два подграфа
В матрицах Q выделены подматрицы Q11 и Q22, лежащие на главной диагонали и включающие элементы qij, характеризующие количество связей между вершинами, включенными в подграфы G1 и G2. Нетрудно убедиться, что сумма элементов подматриц Q11 и Q22 равна удвоенному числу связей внутри подграфов G1 и G2, т.е. связей внутри компонуемых конструктивных модулей низшего уровня.
Подматрицы Q12 и Q21, лежащие вне главной диагонали, напротив, содержат элементы qij, определяющие число связей между вершинами, относящихся к подграфам G1 и G2, т.е. число связей между первым и вторым конструктивным модулями, с которыми интерпретируются подграфы G1 и G2. Выражение (7.1) представляет собой сумму элементов внедиагональной матрицы Qij и равно числу связей между первым и вторым конструктивными модулями низшего уровня, которые должны быть минимизированы. Соответственно (4.2) представляет полную сумму всех элементов внедиагональных подматриц, минимум которой соответствует минимуму числа связей между всеми конструктивными модулями низшего уровня, что и является критерием оптимальности компоновки. Таким образом, в процессе работы алгоритмов разрезания, если строки и столбцы матрицы смежностей перечисляются в порядке принадлежности вершин и компонуемым модулям, должна быть максимизирована сумма элементов диагональных подматриц Qii и минимизирована сумма внедиагональных подматриц Qij, что и соответствует случаю минимума k в (7.2), т.е. минимуму связей между модулями низшего уровня.
Рассмотрим работу последовательного алгоритма разрезания. По матрице смежностей взвешенного графа VG, моделирующего устройства, определяется вершина si с наибольшей локальной степенью gi (степень вершины равна числу инцидентных ей ветвей и численно равна сумме элементов строки и столбца матрицы смежностей, соответствующих вершине). Если таких вершин несколько, то предпочтение может быть отдано любой из них, например имеющей меньший порядковый номер. В подграф G1 включается вершина si и множество вершин S1i, смежных с ней, номера которых можно определить по матрице смежностей. Если мощность множества ½S1i½=N1i, то первый подграф G1(S1, V1) считается сформированным, причем S1i=S1.
Если N1i>N1, то из множества S1i удаляются вершины sj, имеющие минимальное число связей со всеми оставшимися вершинами, что соответствует условию
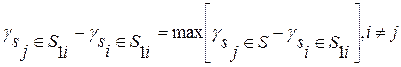 .
.
Как только число вершин в S1i станет равным N1, процесс удаления вершин прекращается и подграф G1 считается сформированным. Если же N1i<N1, то в подграф G1 должны добавляться недостающие вершины, наиболее сильно связанные с вершинами множеcтва S1i. Очередная вершина sj для включения в S1 выбирается из условия
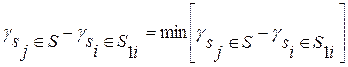 .
.
Включение вершин продолжается до тех пор, пока мощность S1i не станет равной N1. После образования подграфа G1 принадлежащие ему вершины S1 исключаются из исходного графа VG. Получается граф VG*(S*, V*), где S*=S\S1, V*=V\V1. По аналогии с предыдущим, в графе VG* выбирается вершина с наибольшей локальной степенью и с нее начинается построение подграфа G2. Этот процесс повторяется до тех пор, пока граф VG(S, V) не будет разбит на заданное число подграфов z.
Алгоритм 7.2.Последовательный алгоритм разрезания
Шаг 1. Текущий номер формируемого подграфа полагается равным l=1.
Шаг 2. Выбирается вершина si, имеющая максимальное число связей с остальными. Если таких вершин несколько, то среди них выбирают вершину, имеющую максимальное число связей с другой вершиной.
Шаг 3. Выбранная вершина включается в подграф Gl. Если количество вершин в подграфе Gl равно допустимому Nl или количество внешних связей превышает заданное, то переход к шагу 5.
Шаг 4. По матрице смежностей выбирается вершина sj, имеющая максимальное число связей с вершинами, включенными в подграф Gl. Переход к шагу 3.
Шаг 5. Проверяется, все ли подграфы Gl сформированы; если это условие не выполнено, то полагается l=l+1 и переход к шагу 2.
Шаг 6. Оформление результатов разрезания и проверка критерия оптимальности.
Описанный алгоритм компоновки наиболее эффективен для компоновки больших схем, в которых мощность множества ½S½=n значительно превышает число вершин Nl в любом подграфе разбиения Gl.
Основная идея итерационных алгоритмов компоновки заключается в выборе в матрице смежностей взвешенного графа VG или мультиграфа MG таких строк и столбцов, перестановка которых увеличивает сумму элементов в диагональных подматрицах и уменьшит сумму элементов внедиагональных подматриц. Определим изменение числа связей между подграфами Gl и Gm при перестановке двух вершин в этих подграфах: siÎGl и sjÎGm. Число ветвей, связывающих подграфы Gl и Gm, обусловленное связями вершины sj с вершинами подмножества Sl, через элементы матрицы смежностей определяется выражением
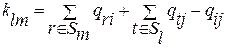 . (7.3)
. (7.3)
После перестановки вершины si в подграф Gm, а вершины sj – в подграф Gl число связей между графами станет равным
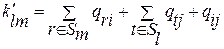 . (7.4)
. (7.4)
Изменение числа связей при перестановке вершин si и sj в подграфы Gl и Gm из (7.3) и (7.4) будет равно
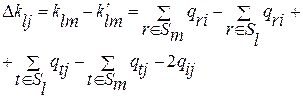 .
.
Перестановка нецелесообразна, если Dkij<0.
Алгоритм 7.3. Итерационный алгоритм разрезания
Шаг 1. Производится предварительное разрезание графа на подграфы, например, с использованием последовательного алгоритма.
Шаг 2. Выделяются диагональные и внедиагональные подматрицы смежностей в соответствии с разрезанием графа.
Шаг 3. Для всех возможных парных перестановок вершин si и sj (i¹j) из подграфов Gl и Gm (l¹m) определяется изменение числа связей между подграфами в результате перестановки Dkij.
Шаг 4. Если есть пары вершин, при перестановке которых Dkij>0, то из них выбирается пара с максимальным значением Dkij, производится перестановка вершин si и sj и переход к шагу 2, иначе шаг 5.
Шаг 5. Оформляются результаты разрезания.
Работа описанного алгоритма приводит к локальному минимуму числа связей между подграфами, так как на каждом шаге выбирается лишь пара вершин, перестановка которых минимизирует число внешних связей. Эффективность алгоритма можно повысить при перестановке групп вершин, однако это приводит к существенному его усложнению. В большинстве случаев работа итерационного алгоритма разрезания прерывается не из-за отсутствия пар вершин, перестановка которых уменьшает число связей между подграфами, а из-за недопустимых временных затрат.
Дата добавления: 2020-03-17; просмотров: 1162;











