Алгоритмы размещения конструктивных модулей
Задача размещения типовых конструктивных модулей в монтажно-коммутационном пространстве (МКП) (например, интегральных микросхем на печатной плате) возникает после решения задачи компоновки радиоэлектронного устройства и решается для каждой полученной в результате компоновки сборной единицы в отдельности [2,3,8]. Для простоты здесь будем рассматривать лишь размещение одногабаритных компонентов.
Исходной информацией при решении задачи размещения являются данные о конфигурации и размерах МКП, количество и геометрические размеры модулей, схема соединений, а также ограничения на взаимное расположение отдельных компонентов, учитывающие особенности разрабатываемой конструкции.
В общем виде задача размещения конструктивных модулей на коммутационной плате формулируется следующим образом. Заданы множество модулей S={s1, …, sn} и множество связей между ними V={u12, …, un, un-1}, а также множество установочных мест (позиций) на коммутационной плате Z={z1, …, zm} (m³n). Найти такое отображение множества S на множестве Z, которое обеспечивает экстремум некоторой целевой функции F.
Основная сложность в постановке задач размещения заключается в выборе целевой функции. Связано это с тем, что одной из главных целей размещения является создание наилучших условий для дальнейшей трассировки соединений, что невозможно проверить без проведения самой трассировки. Однако совместное решение этих задач требует значительных ресурсов ЭВМ (объема памяти и времени решения) и не может быть эффективно осуществлено на современных вычислительных машинах.
Поэтому все применяемые в настоящее время алгоритмы размещения используют промежуточные критерии, которые лишь качественно способствуют решению основной задачи – получению оптимальной трассировки соединений. К таким критериям относятся минимум суммарной взвешенной длины соединений, длина которых больше заданной, минимум числа пересечений проводников, максимальное число соединений между модулями, находящимися в соседних позициях, указанных разработчиком, максимум числа цепей простой конфигурации.
Наибольшее распространение в алгоритмах размещения получил первый критерий, что, как указывалось ранее, объясняется следующими причинами: уменьшение длин соединений улучшает электрические характеристики устройства, упрощает трассировку печатных проводников и снижает трудоемкость изготовления печатных плат; кроме того, он сравнительно прост в реализации.
При размещении, как правило, пренебрегают отличием координат выводов модулей от координат их центров, т.е. используют модель устройства в виде взвешенного графа VG(S, V) (МУ1), мультиграфа MG(S, V) (МУ2) или графа Кенинга KG(S, V) (МУ3).
Так как все эти модели устройства МУ1…МУ3 задаются в ЭВМ с помощью матриц смежностей, между которыми существует простая связь, то в дальнейшем при изучении алгоритмов ограничимся моделями устройств в виде VG – МУ1.
Модели монтажно-коммутационного пространства для решения задачи размещения также используются самые простые: различные варианты дискретных моделей (МКП1) либо в виде взвешенного графа (МКП2), при этом длины межсоединений вычисляются по формулам (3.3) в зависимости от метрики коммутационного пространства.
При практической реализации алгоритмов размещения все соединения между конструктивными модулями сводят к попарно взвешенным связям. Весовые оценки связей pij учитывают такие характеристики схемы, как число электрических цепей между модулями, теплонагруженность компонентов, условия распространения сигналов в цепях и т.д., и могут быть представлены в виде
pij = kBij,
где k – общее количество компонентов, инцидентных электрической цепи, соединяющей элементы si и sj; Bij – коэффициент, указывающий важность минимизации длины данной связи. Например, для рассредоточения теплонагруженных компонентов или компонентов, для которых важны требования электромагнитной совместимости, Bij можно формировать следующим образом:
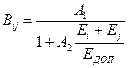 ,
,
где A1, A2 – коэффициенты, определяемые инженером-проектировщиком, исходя из требований к РЭС; Ei, Ej – мощности, рассеиваемые в si- и sj-компонентах (уровни электромагнитного излучения); EДОП – допустимая мощность рассеяния двух соседних компонентов (допустимый уровень напряженности поля).
При уменьшении EДОП либо увеличении Ei, Ej уменьшается Bij, т.е. уменьшается важность связи и компоненты будут размещены далеко друг от друга.
В настоящее время известно значительное число методов решения задачи размещения, из которых можно выделить две основные группы алгоритмов: на первом этапе, полагая коммутационное пространство непрерывным, определяют координаты центров модулей низшего уровня, при которых выбранная целевая функция имеет экстремальное значение. На втором этапе полученные координаты округляются до фиксированных целочисленных значений дискретов рабочего поля, исходя из минимума среднеквадратичной погрешности при округлении. В зависимости от используемой для решения задачи оптимизации целевой функции в непрерывно-дискретных алгоритмах различают методы, основанные на решении нелинейной задачи программирования, и методы, основанные на решении динамической задачи программирования.
В дискретных алгоритмах размещения используют модели МКП вида МКП1 или МКП2 с фиксированными позициями размещаемых модулей, и из различных вариантов закрепления компонентов в фиксированных позициях выбирают тот, который обеспечивает оптимальное значение целевой функции. В зависимости от используемого метода размещения можно выделить следующие группы дискретных алгоритмов: случайного поиска, назначения и эвристические алгоритмы.
Алгоритмы случайного поиска основаны на использовании методов Монте-Карло и относятся к итерационным. На основе датчика случайных чисел выполняют случайную генерацию номеров позиций модулей на МКП с запоминанием лучшего результата в смысле заданного критерия оптимальности размещения. Этот процесс повторяется до тех пор, пока не будет найдено размещение, устраивающее разработчика, либо не будет пересмотрено заданное число вариантов размещения. В зависимости от используемого датчика случайных номеров позиций различают алгоритмы слепого поиска, случайных блужданий, комбинированные. Приведем пошаговое описание алгоритмов слепого поиска.
Алгоритм 7.4. Размещение модулей на плоском МКП методом слепого поиска
Шаг 1. Производится целочисленная нумерация всех возможных позиций размещения модулей в порядке от 1 до m.
Шаг 2. Датчиком случайных чисел с равномерным распределением генерируется n случайных чисел по числу размещаемых модулей в интервале [1, m].
Шаг 3. Производится размещение модулей на случайных номерах позиций в соответствии со значением соответствующего им случайного числа. Вычисляется значение целевой функции F.
Шаг 4. Размещение модулей запоминается, а значение целевой функции полагается равным оптимальному FОПТ, если оно меньше полученного на предыдущей итерации либо если выполняется первая итерация размещения.
Шаг 5. Проверяются условия окончательной работы алгоритма. Если они не выполняются, то переход к шагу 2.
Шаг 6. Производится размещение модулей по наилучшему варианту, полученному в результате испытаний.
В алгоритмах случайных блужданий за счет использования специальных распределений в датчике случайных чисел очередной размещаемый на МКП модуль располагается в дискретах рабочего поля, близких к позициям уже размещенных модулей, с которыми он наиболее сильно связан. Это позволяет сократить затраты машинного времени на поиск оптимального размещения модулей, однако требует наличия у разработчиков соответствующего опыта в выборе параметров распределения для датчика случайных чисел.
Алгоритмы назначения можно разделить на две группы: алгоритмы линейного и квадратичного назначения. В основу алгоритмов линейного назначения положено решение задачи линейного программирования, алгоритмы квадратичного назначения используют методы нелинейного программирования. Ограничимся рассмотрением только первой группы этих алгоритмов.
Перед работой алгоритма выполняют начальное размещение компонентов в монтажно-коммутационном пространстве одним из известных алгоритмов. Для определенности будем полагать, что n конструктивных модулей размещены на m позициях МКП (m³n). Из графа VG(S, V) или MG(S, V), моделирующего устройство, удаляют внутренне устойчивое множество Sa вершин графа (внутренне устойчивым множеством вершин графа называется максимальное количество несмежных вершин графа). Например, для графа, показанного на рис. 7.2, а, б, к внутренне устойчивым можно отнести выделенные на рисунке вершины. Вершины, принадлежащие к внутренне устойчивому множеству вершин графа Sa, исключают из начального размещения. В результате в МКП окажется m–n+a свободных позиций, где a= ½Sa½ – мощность множества Sa.
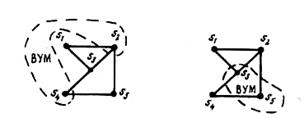 |
а) б)
Рис. 7.2. Внутренне устойчивые множества вершин графа
Для каждого из конструктивных модулей, интерпретируемых вершинами множества Sa, определяем эффективность его размещения на каждой из m–n+a свободных позиций, в простейшем случае равной суммарной длине связей модуля с оставшимися размещенными в МКП модулями множества S'=S\Sa. Так как модули, соответствующие вершинам внутренне устойчивого множества Sa, не связаны между собой, то длина связей dij (jÎ S') модуля sjÎ Sa будет определяться только оставшимися компонентами.
Все dij образуют матрицу D размера a ´ (m–n+a), в которой каждый элемент i-й строки соответствует эффективности установки модуля siÎSa на одну из m–n+a свободных позиций МКП.
Определим функции назначения компонентов из внутренне устойчивого множества на свободные позиции МКП следующим образом:
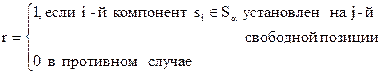
Это позволяет сформулировать задачу размещения на свободных позициях МКП удаленных конструктивных модулей из множества как задачу линейного программирования о назначениях
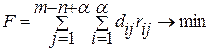 (7.5)
(7.5)
при наличии следующих ограничений:
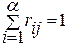 , j = 1, …, m–n+a , j = 1, …, m–n+a
| (на каждой из свободных позиций МКП может быть размещен только один конструктивный модуль) |
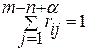 , j = 1, …, a , j = 1, …, a
| (каждый модуль может быть размещен только на одной свободной позиции) |
В результате решения задачи (7.5) получим оптимальное размещение в МКП модулей, соответствующих внутренне устойчивому множеству Sa вершин графа VG, моделирующего устройство. После нахождения оптимального размещения всех компонентов из Sa выделяют следующее внутренне устойчивое множество и размещают его и т.д. Рассмотренный итерационный процесс приводит к постепенному улучшению целевой функции, характеризующей оптимальность размещения. В качестве критерия остановки итерационного процесса можно использовать незначительность изменения целевой функции на двух соседних итерациях.
Алгоритм 7.5. Размещение конструктивных модулей в МКП решением задачи о назначениях
Шаг 1. Выполняется предварительное размещение конструктивных модулей в МКП.
Шаг 2. Формируется очередное внутренне устойчивое множество вершин графа, моделирующего устройство. Компоненты, соответствующие этим вершинам, удаляются с позиций.
Шаг 3. Формируется и решается задача о назначениях в соответствии с (4.5). Размещаются в новых позициях удаленные модули.
Шаг 4. Вычисляется целевая функция размещения.
Шаг 5. Проверяется условие окончания итерационного процесса. Если оно не выполнено, то переход к шагу 2.
Шаг 6. Оформляются результаты решения задачи размещения.
Рассмотренные алгоритмы линейного назначения позволяют найти на каждом шаге оптимальное размещение только для внутренне устойчивого множества модулей. Для получения глобального оптимума достаточно большое число итераций размещения.
Алгоритмы квадратичного размещения более эффективны, однако требуют качественного начального размещения и больших затрат машинного времени.
Из эвристических алгоритмов размещения наибольшую известность получили последовательные и итерационные алгоритмы.
Последовательные алгоритмы основаны на допущении, что для получения минимальной суммарной длины соединений в соседних позициях МКП должны быть размещены модули, максимально связанные друг с другом.
В качестве первоначально размещенных конструктивных модулей выбирают контактные группы разъемов, местоположение которых в коммутационном пространстве задается проектировщиком вручную. Далее на каждом l-м шаге (l= 1, 2, …, n) для установки на коммутационную плату выбирают компонент si из числа еще не размещенных, имеющий максимальную степень связанности с ранее закрепленными элементами Sl-1. Оценку степени связанности si можно выполнить по формуле
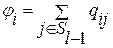 ,
,
где jÎSl-1 – множество индексов конструктивных модулей, закрепленных на предыдущих l-1 шагах, qij – элементы матрицы смежностей.
Если установочные размеры всех размещаемых на плате элементов одинаковы, то выбранный на очередном шаге модуль закрепляют в той позиции zi из числа незанятых, для которой значение целевой функции Fi с учетом ранее размещенных элементов Sl-1 минимально. В частности, если критерием оптимальности является минимум суммарной взвешенной длины соединений, то
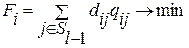 ,
,
где dij – расстояние между ДРП zi для установки компонента si и позицией zi размещенного ранее компонента; t – множество незанятых позиций после (l-1) шага алгоритма.
Алгоритм 7.6. Последовательный алгоритм размещения конструктивных модулей в МКП
Шаг 1. Производится первоначальное размещение ряда конструктивных модулей и контактных групп разъема. Размещаемые компоненты заносятся в множество Sp.
Шаг 2. Неразмещаемые конструктивные модули ранжируются по количеству связей с модулями, включенными в множество Sp.
Шаг 3. Выбирается модуль si, имеющий максимальное количество связей ji с модулями множества Sp, и для него определяется свободный ДРП zt, при размещении в котором si длина связей будет минимальной.
Шаг 5. Проверяется, все ли конструктивные модули размещены в МКП, если нет, то переход к шагу 2.
Шаг 6. Вычисляется результирующая длина соединений; оформляется результат размещения.
В итерационных алгоритмах для улучшения первоначального размещения компонентов в коммутационном пространстве, полученного, например, при работе последовательного алгоритма, вводят процесс перестановки пар компонентов с целью дальнейшей минимизации длины соединений. Изменение длины соединений при перестановке местами конструктивных модулей низшего уровня si и sj, закрепленных в t-й и r-й позициях, может быть определено по формуле
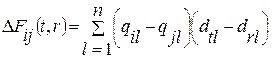 .
.
На каждом шаге итерационного алгоритма размещения выбирается очередной компонент перестановки si, начиная с закрепленного на первой позиции, и для него отыскивается на МКП второй компонент sj, для которого величина DF>0 и максимальна.
Аналогичным образом оценивается целесообразность перестановки очередного компонента, находящегося на второй, третьей и т.д. позициях, до тех пор, пока не будут просмотрены все m позиций коммутационной платы. После завершения просмотра производится парная перестановка компонентов si и sj, для которых изменение длины соединений максимально. На этом итерация заканчивается. В последующих итерациях описанный процесс повторяется, пока не будет выполнено заданное число итераций, либо не будет израсходован ресурс машинного времени, либо изменение суммарной взвешенной длины соединений на последней итерации не станет меньше заданного.
Алгоритм 7.7. Итерационный алгоритм размещения
Шаг 1. Производится первоначальное размещение конструктивных модулей в МКП.
Шаг 2. Определяются ДРП и модули, перестановка которых допустима по конструктивным соображениям. Множество SП={s1, …, sn} переставляемых компонентов упорядочивается.
Шаг 3. Выбирается очередной компонент из множества SП и определяется изменение длины соединений, если его поменять местами с остальными модулями множества SП. Запоминается наилучший результата перестановки.
Шаг 4. Проверяется, для всех ли модулей из множества SП проверены парные перестановки; если нет, то возврат к шагу 3.
Шаг 5. Осуществляется перестановка пары модулей, обеспечивающих максимальное уменьшение длины соединений.
Шаг 6. Проверяется условие окончательной работы алгоритма; если они не выполняются, то переход к шагу 2.
Шаг 7. Оформляются результаты размещения.
Дата добавления: 2020-03-17; просмотров: 1204;











