Определение приведенных масс и приведенных моментов инерции.

ДИНАМИЧЕСКАЯ МОДЕЛЬ МЕХАНИЗМА

Звено приведения.

Определение приведенных масс и приведенных моментов инерции.

Определение приведенных сил и приведенных моментов сил.

Звено приведения.

Мы начинаем рассматривать вторую основную задачу динамики механизмов и машин, связанную с определением режима движения механизма под действием приложенных к нему сил и установлением способов, обеспечивающих заданные режимы движения механизма.

Механизм машинного агрегата обычно является многозвенной системой, нагруженной силами и моментами сил, приложенными к различным ее звеньям. Определение закона движения такой сложной многозвенной системы представляет собой трудную задачу. Мы с вами рассматриваем чаще всего механизмы, которые имеют одну степень свободы (W = 1). Это значит, что, прежде всего надо определить закон движения всего лишь одного из его звеньев, которое тем самым будет являться начальным звеном. Такая постановка задачи приводит к мысли, заменить весь сложный многозвенный механизм условным звеном. Условное звено, заменяющее весь механизм называется звеном приведения.

В качестве звена приведения удобней всего взять ведущее звено.

		К звену приведения предъявим следующие требования – пусть его момент инерции Iп и момент сил Мп , которым оно загружено, будут такими, чтобы закон движения звена приведения получился полностью совпадающим с законом движения ведущего звена, т.е. ωп = ω1

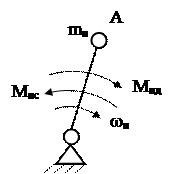Таким образом, звено приведения будет являться динамической моделью всего механизма.

Определение приведенных масс и приведенных моментов инерции.

Н.И.Мерцалов, в начале прошлого века, предложил для определения приведенных масс и приведенных моментов инерции, использовать закон сохранения энергии. Запишем уравнение «живых» сил, выражающий закон сохранения энергии.

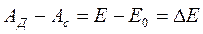
где: 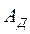- работа всех движущих сил;

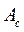- работа всех сил сопротивления;

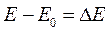- приращение кинетической энергии за определенный промежуток времени.

При приведении масс это равенство должно соблюдаться, а это значит должно соблюдаться и равенство кинетических энергий звена приведения и всего мехнаизма

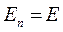
В общем случае при плоскопараллельном движении звеньев кинетическая энергия механизма будет определяться по выражению

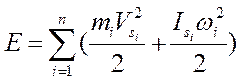
где: 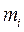- масс i-го звена;

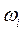- угловая скорость i-го звена;

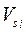- скорость центра тяжести i-го звена;

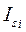- момент инерции i-го звена относительно центральной оси.

Кинетическая энергия звена приведения с массой 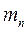в точке А (см. рис.)

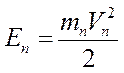
из этих уравнений следует

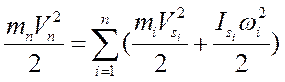
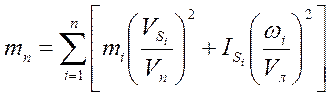
В то же время кинетическая энергия звена приведения с моментом инерции I_п

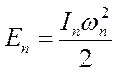
при 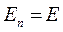следует

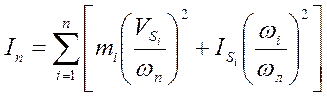
Так как скорости точек и звеньев, стоящие в числителе приведенных выражений, определяются через угловую скорость ведущего звена, стоящую в знаменателе, то можно сделать вывод:

Приведенная масса и приведенный момент инерции не зависит от закона движения ведущего звена, а зависят от размеров звеньев, массы, размещения масс по звеньям и угла поворота ведущего звена.