Теоретические основы дробления и измельчения
Определение величины энергии, затрачиваемой на преодоление внутренних сил сцепления зерен при их разрушении, является одной из основных задач в теории дробления и измельчения.
Для изменения междуатомного расстояния в структурной решетке кристаллического твердого тела требуется работа деформации (сжатие, растяжение, сдвиг или изгиб). В пределах упругости атомы возвращаются в свое первоначальное положение. В горных породах предел упругости и предел разрушения часто совпадают.
В зернах горных пород действуют силы сцепления внутри кристаллов и силы между отдельными кристаллами. Они имеют одинаковую физическую природу и различаются между собой только величиной. Первые силы во много раз превышают вторые.
Все горные породы содержат в себе зоны ослабления (дефекты) структуры микро- и макротрещины, что в большой степени влияет на зерновой состав продуктов измельчения и удельный расход энергии.
Таким образом, величина внутренних сил взаимного сцепления частиц горной породы, которые необходимо преодолеть при ее дроблении или измельчении, определяется природой и структурой кристаллов, входящих в состав этой породы, а также величиной дефектов структуры, микро- и макротрещин.
Процесс дробления и измельчения горных пород вначале происходит по трещинам и наиболее слабым местам после перехода за предел прочности нормальных и касательных напряжений, возникающих в материале. Затем идет разрушение более однородной массы. При весьма тонком измельчении сопротивление материала разрушению резко возрастает.
Энергия, идущая на дробление и измельчение, расходуется на упругую деформацию разрушаемых зерен, рассеивается в окружающее пространство в виде тепла и на образование новой поверхности и превращается в свободную поверхностную энергию измельченных зерен.
По Кирпичеву — Кику, расход энергии на дробление материала пропорционален его объему или массе (весу).
При деформациях сжатия, растяжения и изгиба, когда действуют нормальные напряжения, работа разрушения одного крупного куска с малой степенью дробления пропорциональна изменению его объема Δv
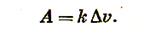 (3.3)
(3.3)
Так как Δv пропорционально первоначальному объему куска Δv = k1v, то
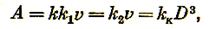 (3.4)
(3.4)
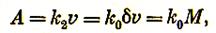 (3.5)
(3.5)
где k, k1, k2, kк и k0 — коэффициенты пропорциональности; М — масса (вес) куска; D — диаметр куска.
Таким образом, работа дробления пропорциональна объему или массе дробимого зерна.
Уравнения (3.4) и (3.5) справедливы при дроблении крупных кусков с малой степенью дробления, когда величиной энергии, расходуемой на образование новой поверхности, можно пренебречь.
Предположим, что в дробление поступает Gтисходного материала, состоящего из зерен различной крупности и формы.
Определим работу дробления Gт материала по отдельным стадиям (условия аналогичны предыдущему случаю).
Работа дробления Gт материала, состоящего из N кусков одинаковой массы М, равна (по формуле Кирпичева—Кика):
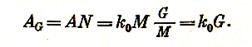
При i = rn работа дробления по стадиям составит:
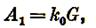
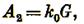
………..
………..
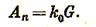
Работа дробления Gтматериала при общей степени дробления i равна
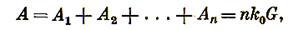 (3.6)
(3.6)
где - 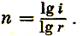
Подставив п в формулу (3.59), получим
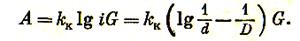 (3.7)
(3.7)
По Риттингеру работа, затраченная на измельчение, пропорциональна величине вновь образованной поверхности. Предположим, что зерно в виде куба с ребром D разрушается до куба с ребром d. Число полученных кубов 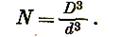
Поверхности куба S1 и полученных кубов S2соответственно равны: 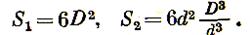
Вновь образованная поверхность
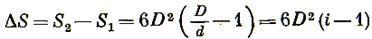
где i — степень измельчения.
Работа, расходуемая на измельчение этого зерна, равна
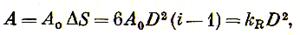 (3.8)
(3.8)
где А0— работа образования единицы новой поверхности.
Работа измельчения пропорциональна поверхности дробимого зерна.
Удельная работа А0образования новой поверхности зависит от природы материала, его крупности, степени и способа измельчения.
Закон Риттингера справедлив при измельчении полезных ископаемых с большими степенями, когда энергия расходуется на образование новой поверхности. В этом случае энергия расходуется в основном на деформацию сдвига при переходе касательных напряжений за предел прочности. Закон Риттингера не учитывает изменения сопротивления материала измельчению в данной мельнице по мере уменьшения его крупности.
Предположим, что в измельчение поступает Q исходного материала, состоящего из зерен различной крупности и формы. Пусть D и d — средние диаметры зерен до и после измельчения; во всех стадиях одинаковая степень измельчения r, а число стадий равно п, т. е.
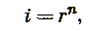
где i — общая степень измельчения.
Тогда работу измельчения Q тонн материала по отдельным стадиям согласно закону Риттингера можно определить по формулам.
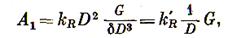
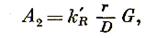
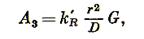
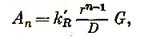
где δ — плоскость материала; 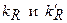 - коэффициенты пропорциональности.
- коэффициенты пропорциональности.
Общая работа измельчения
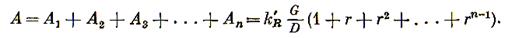
Сумма членов геометрической прогрессии со знаменателем г равна
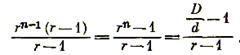
Следовательно,
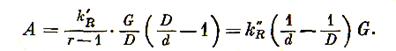 (3.9)
(3.9)
По Ребиндеру, работа, затрачиваемая на измельчение материала, представляет собой сумму работ, расходуемых на его деформацию и на образование новой поверхности:
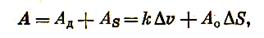 (3.10)
(3.10)
где АД— работа упругих деформаций; АS — работа образования новой поверхности; k — коэффициент пропорциональности, представляющий собой работу деформации в единице деформируемого объема зерна; Δv — изменение объема деформируемого зерна; А0— коэффициент пропорциональности, представляющий собой затрату работы на образование единицы новой поверхности; ΔS — вновь образованная поверхность при измельчении.
По Ребиндеру, процесс упругой деформации тела характеризуется наведением в нем новой поверхности (трещины). При предельной объемной концентрации в теле трещин наступает его разрушение. Между процессами упругой деформации и разрушения с точки зрения образования поверхности разницы не существует.
Установленная П. А. Ребиндером зависимость позволяет рассматривать процесс измельчения как единое целое и в то же время анализировать его. Работа образования новой поверхности АS является полезной, а работа упругих деформаций AД — потерей.
Тогда коэффициент полезного процесса измельчения
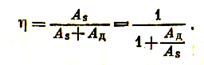 (3.11)
(3.11)
Таким образом, для повышения к. п. д. измельчения следует:
- по возможности увеличивать АS (т. е. измельчать материал при максимальном перенапряжении);
- применять поверхностно-активные вещества, которые снижают предел упругих напряжений.
Между дроблением крупных кусков с малой степенью, описываемым уравнением (3.3), и измельчением с большой степенью, описываемым уравнением (3.8), имеются крупное, среднее и мелкое дробление со средними степенями дробления, для которых необходимо учитывать обе составляющие уравнения (3.10). Для превращения правой части этого уравнения в одночлен сделано допущение, что работа, расходуемая на дробление, пропорциональна среднему геометрическому из объема и поверхности разрушаемого зерна [1] и составляет
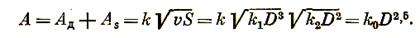 (3.12)
(3.12)
Формула (3.12) выражает работу на дробление по Бонду.
В дальнейшем принимается, что измельчение зерна от крупности D до крупности d производится в n приемов с постоянной однократной степенью измельчения r. Тогда в первом приеме измельчения получится r3 зерен размером D/r и затрачивается работа
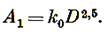
Соответственно во втором и n-мприемах измельчения:
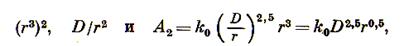
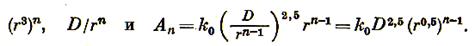
Общая работа, расходуемая на измельчение,
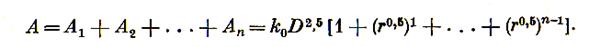
Сумма геометрической прогрессии со знаменателем r0,5
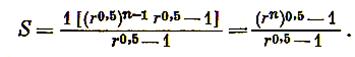
Следовательно,
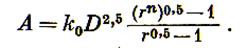 (3.13)
(3.13)
Определим работу на измельчение Gт материала.
Число зерен кубической формы с ребром D в Gт материала
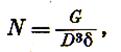
где δ — плотность материала.
Тогда работа на измельчение Gт материала
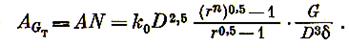
Так как 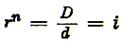 , то
, то
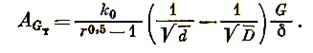 (3.14)
(3.14)
В этой формуле неизвестными являются k0 и r.
Пользуясь выражением (3.14), можно приближенно определить работу для крупного, среднего и мелкого дробления со средними степенями дробления.
Формулы (3.9), (3.7), (3.10), (3.14) можно использовать для сравнительной оценки процессов дробления (измельчения), когда не нужно знать величины коэффициентов пропорциональности.
Дата добавления: 2016-06-18; просмотров: 3453;











