Переход от одной математической формы описания к другой

Рассмотрим пример перехода от одной формы представления к другой.

Дифференциальное уравнение объекта имеет вид:

.

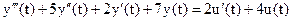Необходимо описать рассматриваемый объект с помощью известных форм.

Запишем дифференциальное уравнение объекта в следующем виде:

.

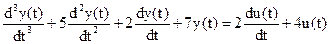Тогда, используя оператор дифференцирования 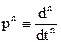, запишем уравнение объекта в операторном виде:

.

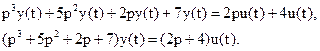По формуле (1.7) передаточная функция в операторном виде для заданного объекта:

.

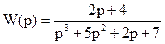Заменив оператор дифференцирования 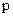на оператор Лапласа 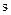запишем передаточную функцию объекта в изображения Лапласа:

.

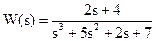В теории управления пространство состояний - один из основных методов описания поведения динамической системы.

Иногда возникает необходимость прямого и обратного перехода от записи системы в виде передаточной функции к форме описания с помощью пространства состояний. Прямой переход в такой задаче неоднозначен, т.е. существует бесконечное множество троек матриц, в то время как обратный переход однозначен. Существует три стандартных схемы перехода от передаточной функции к пространству состояний: последовательная схема, параллельная и нормальная.

Рассмотрим методику перехода по каждой схеме.