Математические способы описания систем: дифференциальные уравнения, передаточные функции, пространство состояния. Переход от одной формы к другой.

Способы представления систем управления

Для исследования любой системы управления используется ее модель.

Модель — это объект или явление, в достаточной степени повторяющие свойства моделируемого объекта или явления (прототипа), существенные для целей конкретного моделирования, и опускающие несущественные свойства, в которых они могут отличаться от прототипа.

Виды моделей:

1 на естественном языке

2 на специальном языке

2.1 научные

2.1.1 математические формулы

2.1.2 алгоритмы

3 технические

3.1 техкарты

3.2 программы

4 Смешанные

4.1 таблицы

4.2 графы

4.2.1 деревья

4.2.2 сети

4.2.3 блок - схемы

4.3 схемы

4.4 карты

5 Наглядные (выраженные на языке представления)

5.1 рисунки

5.2 чертежи

5.3 графики

5.4 фотографии

В теории управления для исследования систем используются математические и смешанные (графические) способы описания систем.

Математические способы описания систем: дифференциальные уравнения, передаточные функции, пространство состояния. Переход от одной формы к другой.

В теории управления широко применяется несколько математических способов описания системы управления, а точнее ее математической модели. Одномерные одноканальные системы (или объекты) обычно описывают дифференциальным уравнением, связывающим входной и выходной сигнал системы:

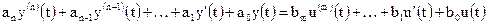, (1.1)

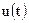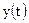здесь и - входной и выходной сигналы системы,

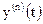- производная сигнала 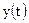n-го порядка;

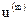- производная сигнала 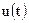m-го порядка;

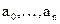- коэффициенты при выходном сигнале и его производных;

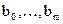- коэффициенты при входном сигнале и его производных.

При составлении дифференциального уравнения системы следует учитывать следующие замечания: выходной сигнал и его производные записываются в левой части уравнения, а входной сигнал и его производные – в правой; условие 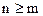является условием физической реализуемости системы.

В случае многоканальной системы используют систему дифференциальных уравнений, записанную в виде нормальной формы Коши, т.е.

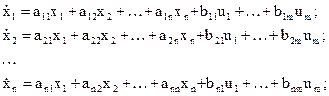(1.2)

здесь 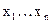- выходные сигналы системы,

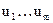- входные сигналы системы.

Такую систему дифференциальных уравнений относительно первых производных часто записывают в матричной форме:

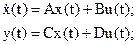(1.3)

здесь 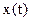- вектор переменных состояния;

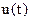- вектор входных переменных;

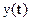- вектор выходных переменных;

A - матрица коэффициентов системы;

B - матрица входных коэффициентов (матрица управления);

C - матрица выходных коэффициентов;

D- матрица коэффициентов пропорциональных каналов (матрица компенсации).

При этом размерность матриц будет определяться размерностью исходного дифференциального уравнения. Способ описания системы управления с помощью дифференциальных уравнений в матричной форме называется методом пространства состояний.

Если при составлении дифференциального уравнения процедуру вместо знака дифференцирования (например 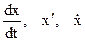) использовать оператор дифференцирования, то полученное уравнение будет называться дифференциальным уравнением в операторном виде. Так, для уравнения (1.1) запишем:

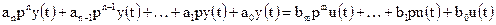, (1.4)

здесь 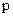- оператор дифференцирования, т.е. .

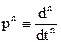В общем виде дифференциальное уравнение в операторном виде можно записать:

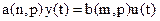, (1.5)

тогда уравнение относительно выходного сигнала будет иметь вид:

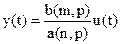. (1.6)

Следующим способом описания системы управления является передаточная функция. Передаточная функция, связывающая входной и выходной сигналы времени, называется операторной передаточной функцией, и, соответственно (1.6), записывается как:

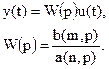(1.7)

Если от дифференциальных уравнений перейти к уравнениям в изображениях Лапласа, т.е оператор дифференцирования 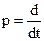заменить на оператор Лапласа 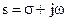, тогда вместо операторной передаточной функции следует говорить о передаточной функции в изображениях Лапласа:

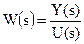, (1.8)

здесь 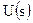и 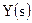изображения Лапласа сигналов 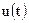и 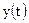, s – переменная преобразования Лапласа.

Таким образом, в теории управления для описания математической модели системы используются следующие формы:

1. дифференциальное уравнение,
2. дифференциальное уравнение в операторном виде,
3. операторная передаточная функция,
4. передаточная функция в изображениях Лапласа,
5. пространство состояний.