Обработка результатов прямых однократных измерений
Прямые однократные измерения являются самыми массовыми и проводятся, если: при измерении происходит разрушение объекта измерения, отсутствует возможность повторных измерений, имеет место экономическая целесообразность. Прямые однократные измерения возможны лишь при определенных условиях:
1) объем априорной информации об объекте измерения такой, что определение измеряемой величины не вызывает сомнений;
2) изучен метод измерения, его погрешности либо заранее устранены, либо оценены;
3) средства измерений исправны, а их метрологические характеристики соответствуют установленным нормам.
За результат прямого однократного измерения принимаем полученную величину. До измерения должна быть проведена априорная оценка составляющих погрешности. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается, как правило, равной 0,95.
Методика обработки результатов прямых однократных измерений приведена в рекомендациях МИ 1552–86 «ГСИ. Измерения прямые однократные. Оценивание погрешностей результатов измерений». Данная методика применима при выполнений следующих условий: составляющие погрешности известны, случайные составляющие распределены по нормальному закону, а неисключенные систематические, заданные своими границами θ, – равномерно.
Составляющими погрешности прямых однократных измерений являются:
1) погрешности средства измерений (СИ), рассчитываемые по их метрологическим характеристикам;
2) погрешность используемого метода измерений;
3) погрешность оператора.
Названные составляющие могут состоять из неисключенных систематических и случайных погрешностей. При наличии нескольких систематических погрешностей доверительная граница результата измерения рассчитывается по формуле:
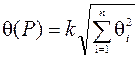 , (34)
, (34)
где k – коэффициент, зависящий от P, равный 0,95 при P=0,9 и 1,1 при P=0,95.
Случайные составляющие погрешности результата измерения выражаются либо СКО Sx, либо доверительными границами. В первом случае доверительная граница случайной составляющей погрешности результата прямого однократного измерения определяется через его СКО:
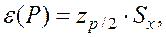 (35)
(35)
где zp/2 – точка нормированной функции Лапласа, при вероятности Pд. При доверительной вероятности Рд=0,95 zp/2 принимают равным 2, при Р=0,99 zp/2=2,6.
Если СКО определены экспериментально при небольшом числе измерений (n<30), то в данной формуле вместо коэффициента zp следует использовать коэффициент Стьюдента, соответствующий наименьшему числу измерений.
Найденные значения θ и ε(P) используются для оценки погрешности результата прямого однократного измерения. Суммарная погрешность результата измерения определяется в зависимости от соотношения θ и Sx.
Если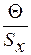 <0,8, то неисключенными систематическими погрешностями следует пренебречь и принять в качестве погрешности результата измерения доверительные границы случайных погрешностей.Если
<0,8, то неисключенными систематическими погрешностями следует пренебречь и принять в качестве погрешности результата измерения доверительные границы случайных погрешностей.Если 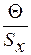 >8, то случайными погрешностями пренебрегают и принимают в качестве погрешности результата измерения границы неисключенных систематических погрешностей.Если 0,8<=
>8, то случайными погрешностями пренебрегают и принимают в качестве погрешности результата измерения границы неисключенных систематических погрешностей.Если 0,8<= 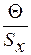 <=8, то доверительная граница погрешности результата измерений вычисляется по формуле:
<=8, то доверительная граница погрешности результата измерений вычисляется по формуле: 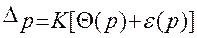 (36) где К – коэффициент, значение которого для доверительной вероятности 0,95 равно 0,76; для доверительной вероятности 0,99 значение коэффициента K равно 0,83.
(36) где К – коэффициент, значение которого для доверительной вероятности 0,95 равно 0,76; для доверительной вероятности 0,99 значение коэффициента K равно 0,83.
Пример
При однократном измерении физической величины получено показание средства измерения x=10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает следующей априорной информацией о средстве измерений и условиях выполнения измерений: класс точности средства измерений 2; пределы измерений 0…50; значение аддитивной поправки qа=–0,5, СКО Sx=0,1.
Пример решения
1.1 Анализ имеющейся априорной информации: имеется класс точности средства измерения, аддитивная поправка, СКО.
1.2 При измерении получено значение: x=10.
1.3 За пределы неисключенной систематической погрешности принять пределы допускаемой абсолютной погрешности прибора, которые находят как:
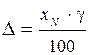 (37)
(37)
где xN – нормирующее значение, в данном случае равное диапазону измерения средства измерения xN =50; g – нормируемый предел допускаемой приведенной погрешности, который определяют из класса точности средства измерения g=2,0 %.
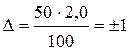 (38)
(38)
Таким образом, θ = ±1.
1.4. Находят границы случайной составляющей погрешности измерения:
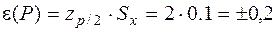 (39)
(39)
1.5. Определяют суммарную погрешность результата измерения.
Так как θ>8Sx, то за границы суммарной погрешности принимают границы неисключенной систематической погрешности Δp= 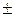 1
1
1.7. В результат измерения вносят поправку:
X=x+θa=10+0,5=10,5 (40)
1.8. Записывают результаты измерений: 10,5±1,0; PД=0,95.
Содержание отчета
1. Цель и задачи работы.
2. Краткая характеристика основных параметров микроклимата помещений.
3. Краткая характеристика прибора ТКА-ПКМ 50
4. Методика измерения подвижности воздуха.
5. Обработка результатов прямых однократных измерений.
6. Выводы по работе.
Дата добавления: 2016-06-18; просмотров: 10776;











