Генеральная совокупность и выборка
Полная совокупность объектов, или, точнее, совокупность значений какого-то признака объектов, называется генеральной совокупностью. Основной задачей математической статистики является исследование генеральной (полной) совокупности статистически, то есть выяснение (оценка) вероятностных свойств совокупности: распределения, числовых характеристик и т. д.
Однако полное исследование генеральной совокупности обычно практически невозможно или неэкономно. Например, при проверке электролампы одним из её показателей качества считается общее время работы (до сгорания). Аналогичная ситуация имеет место и при проверке качества консервов, снарядов и т. д. Всеобщее исследование (проверку) применяют, как правило, редко. Например, всеобщую перепись населения проводят примерно через 10 лет.
Обычно из генеральной совокупности делают выборку, то есть исследуют только часть её объектов. С помощью выборки оценивают генеральную совокупность по вероятностным свойствам. Чтобы оценки были достоверными, выборка должна быть представительной, то есть её вероятностные свойства должны совпадать или быть близкими к свойствам генеральной совокупности. Для этого надо в достаточном объёме выбирать объекты для исследования случайным образом, то есть гарантировать всем объектам генеральной совокупности одинаковую вероятность подвергнуться исследованию.
Случайно выбранный объект после проверки нужного признака можно возвратить (возвратная или повторная выборка) или не возвратить (безвозвратная или бесповторная выборка) обратно в генеральную совокупность. В первом случае получаем более независимую и представительную выборку.
Часто под генеральной совокупностью понимают и сами исследуемые случайные величины, их значения. Совокупность полученных в испытаниях значений также называется выборкой и обрабатывается статистически. Методы статистической обработки повторной и бесповторной выборок аналогичны.
При исследовании объектов можно фиксировать или измерять значение одного или нескольких признаков (величин). Соответственно говорят об одномерной, двумерной, трехмерной и т. д. выборках. Вначале рассмотрим обработку одномерных выборок.
2.1.2 Вариационный ряд
Выбор объекта из генеральной совокупности и измерение значения признака называется статистическим наблюдением. Результаты наблюдений фиксируют в протоколе или дневнике наблюдений в порядке их появления.
Выборка будет намного наглядней, если все её элементы упорядочить по возрастанию или по убыванию признака. Но в выборке одно значение (варианта) может встречаться несколько раз, и поэтому целесообразно результаты записать в виде таблицы, в первом столбце которой находятся всевозможные значения xi генеральной совокупности (или случайной величины) X, а во втором – числа ni , то есть частоты появления i-го значения. Такую таблицу называют вариационной таблицей или вариационным рядом.
Для составления вариационного ряда нужно:
1) найти минимальное (xmin) и максимальное (xmax) значения в выборке;
2) в первый столбец таблицы записать полученные (различные) значения случайной величины (генеральной совокупности), начиная с xmin и кончая xmax , в порядке их возрастания;
3) подсчитать количество одинаковых значений xi и записать соответствующее им число ni;
4) подсчитать общее количество элементов в выборке (объём выборки) n и сравнить его с найденным по формуле:
n= 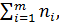 (2.1)
(2.1)
где m – количество различных значений в вариационном ряде. Если условие (2.1) не выполнено, то повторить все пункты, начиная с третьего.
Пример вариационного ряда по значениям дан в табл. 1 (выборка А).
Если количество вариантов m слишком велико или близко к объёму выборки, то целесообразно составить вариационный ряд по интервалам значений генеральной совокупности, его составляют по выборке из непрерывной генеральной совокупности.
Вариационный ряд по интервалам значений можно получить с помощью приведённого выше алгоритма, где во втором пункте следует:
- заполнить первый столбец таблицы интервалами значений X генеральной совокупности;
- все интервалы выбирать одинаковой длины таким образом, чтобы xmin вошло в первый, а xmax – в последний интервал. Обычно начало интервала входит в интервал, а его конец, – не входит.
В остальных пунктах алгоритма следует слово “значение” заменить словом “интервал”. Пример вариационного ряда по интервалам смотри в таблице 2 (выборка В).
2.1.3 Графики вариационных рядов
Значения генеральной совокупности будут сравнимыми, если использовать относительные частоты ( частости) ni/n, их обычно используют при построении графиков. Сумма всех частот должна быть равна единице [см. формулу (2.1)], так как они являются аналогами вероятности:
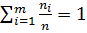 . (2.2)
. (2.2)
Используют два вида графиков выборочного распределения (вариационного ряда): полигон (частот) и гистограмму. Если вариационный ряд составлен по значениям, то полигон строят из отрезков, соединяющих точки, координатами которых являются значения xi и соответствующие относительные частоты ni/n (см. рисунок 17). При построении гистограммы над каждым значением xi строят прямоугольник, высота которого пропорциональна соответствующей относительной частоте ni/n (см. рис.18 ).
Если вариационный ряд составлен по интервалам, то в качестве значений xi следует рассматривать середины интервалов (см. рисунки 20, 21).
2.1.4 Эмпирическая функция распределения
Каждая генеральная совокупность имеет функцию распределения F(x) [см. формулу (1.19)], которая обычно неизвестна. По выборке можно найти эмпирическую функцию распределения F*(x), где на основании закона больших чисел (теорема Бернулли) вместо вероятностей pi берутся относительные частоты ni/n, так как они при n → 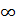 стабилизируются около значений вероятности pi событий X = xi (это статистическое определение вероятности). Процесс нахождения эмпирической функции распределения F*(x) аналогичен процессу нахождения функции распределения F(x) дискретной случайной величины X [см. п. 1.2.3, формулы (1.20) и (1.21)]:
стабилизируются около значений вероятности pi событий X = xi (это статистическое определение вероятности). Процесс нахождения эмпирической функции распределения F*(x) аналогичен процессу нахождения функции распределения F(x) дискретной случайной величины X [см. п. 1.2.3, формулы (1.20) и (1.21)]:
F*(x) = 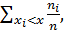 (2.3)
(2.3)
F*(x)= 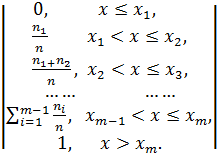 (2.4)
(2.4)
Значениями эмпирической функции распределения F*(x) [формула (2.4)] являются так называемые накопленные частоты (смотри таблицы 1 и 2). График эмпирической функции распределения строят так же, как и график функции распределения F(x) дискретной случайной величины (см. рисунок 3).
Если вариационный ряд составлен по интервалам значений и в качестве представителя интервала берётся его середина, то эмпирическая функция составляется так же, как по вариационному ряду по значениям. Таким образом, получаем ломаную линию, являющуюся довольно хорошим приближением графика функции распределения непрерывной случайной величины (сравни рисунки 5 и 22). Такой график является точным, если все значения в каждом интервале распределены равномерно.
2.1.5 Числовые характеристики выборки
2.1.5.1 Среднее арифметическое
Среднее арифметическое 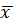 определяется по формуле:
определяется по формуле:
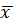 =
= 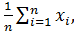 (2.5)
(2.5)
где xi – элементы выборки, n – её объём. Если объём n выборки и xi не слишком велики, то расчёт “вручную” по этой формуле не вызывает трудности. Для больших выборок необходимо прибегнуть к помощи микрокалькулятора или ЭВМ. Выборочное среднее 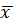 является оценкой математического ожидания (или среднего) генеральной совокупности Х.
является оценкой математического ожидания (или среднего) генеральной совокупности Х.
Если составлен вариационный ряд, в котором могут повторяться одинаковые значения xi, то следует использовать следующую формулу:

где xi – неодинаковые значения (варианты) случайной величины в количестве m, ni – соответствующие им частоты, n – общий объём выборки.
Если вариационный ряд составлен по интервалам значений, то в роли xi в формуле (2.6) используют середины интервалов.
2.1.5.2 Дисперсия выборки
Дисперсию выборки обозначим через 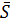 2. Для вычисления выборочной дисперсии
2. Для вычисления выборочной дисперсии 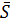 2 используются формулы:
2 используются формулы:
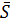 2=
2= 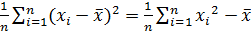 2, (2.8)
2, (2.8)
где n – общий объём выборки;
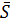 2=
2= 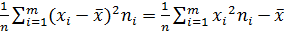 2, (2.9)
2, (2.9)
где m – количество неодинаковых значений xi, ni – их частоты (повторения).
2.1.5.3 Стандартное отклонение
Выборочное стандартное, или среднеквадратичное, отклонение определяется как квадратный корень из дисперсии:
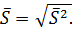 (2.10)
(2.10)
2.1.5.4 Мода
Если вариационный ряд составлен по значениям генеральной (дискретной) совокупности, то модой выборки является значение, имеющее максимальную частоту. Если вариационный ряд составлен по интервалам значений генеральной совокупности, то мода вычисляется по следующей приближённой формуле:
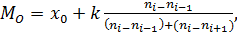 (2.11)
(2.11)
где x0 – начало модального интервала, то есть интервала, имеющего максимальную частоту, k – длина модального интервала, ni - частота модального интервала, 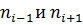 – частоты соответственно предшествующего и последующего за модальным интервалом.
– частоты соответственно предшествующего и последующего за модальным интервалом.
2.1.5.5 Медиана
Медианой выборки является значение серединного элемента вариационного ряда. Если вариационный ряд составлен по значениям генеральной совокупности, то при нечётном объёме выборки n медиана – это действительное значение серединного элемента, а при n чётном - среднее арифметическое двух серединных элементов.
Если вариационный ряд составлен по интервалам значений, то медиана вычисляется по следующей приближённой формуле:
Ме = 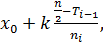 (2.12)
(2.12)
где x0 – начало медианного интервала, то есть интервала, в котором содержится серединный элемента; k – длина медианного интервала; n – объём выборки; Ti-1 – сумма частот интервалов, предшествующих медианному; ni – частота медианного интервала.
В следующих задачах необходимо для заданных вариационных рядов:
· вычислить относительные и накопленные частоты (частости);
· построить графики вариационного ряда (полигон и гистограмму);
· составить эмпирическую функцию распределения;
· построить график эмпирической функции распределения;
· вычислить числовые характеристики вариационного ряда:
¾ среднее арифметическое 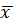 ;
;
¾ дисперсию 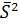 ;
;
¾ стандартное отклонение S,
¾ моду Mо;
¾ медиану Ме.
Задача 2.1
Имеется выборка A, её вариационный ряд xi и частоты появления xi (ni) и т. д. (см. таблицу 1).
Таблица 1. Выборка A
| xi | ni | относительные частоты ni/n | Накопленные относительные частоты |
| xmin =0 | 0,0506 | 0,0506 | |
| 0,1646 | 0,2152 | ||
| 0,1772 | 0,3924 | ||
| 0,3038 | 0,6962 | ||
| 0,2025 | 0,8987 | ||
| 0,0380 | 0,9367 | ||
| 0,0380 | 0,9747 | ||
| xmax =7 | 0,0253 | 1,0000 | |
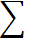
| n=79 | 1,0000 | - |
Все относительные частоты вычисляем с одинаковой точностью. При построении графиков изображаем на оси x значения с 0 по 7 и на оси ni/n – значения с 0 по 0,3038 (рисунки 17 и 18).
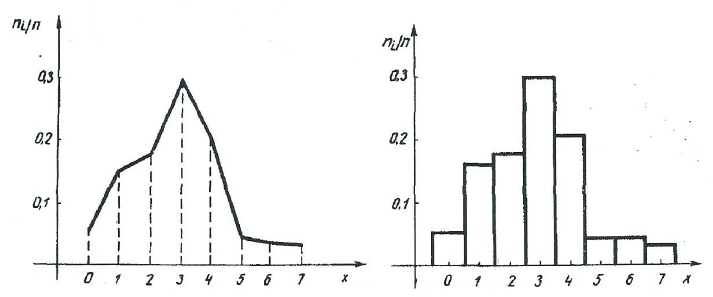
Рисунок 17. Полигон вариационного Рисунок 18. Гистограмма ф ряда выборки A вариационного ряда выборки A
Полигон строится для точек xi, а гистограмма – для интервалов, где xi являются их серединами.
Эмпирическую функцию распределения F*(x) находим, используя формулу (2.4) и накопленные частоты, из таблицы 1. Имеем:
F*(x) = 
При построении графика F*(x) откладываем значения функции в интервале от 0 до 1 (рис. 19).
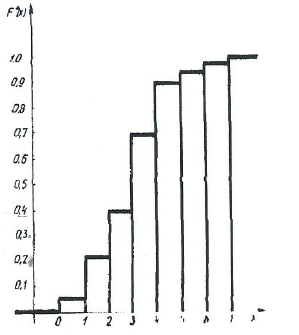
Рисунок 19. График эмпирической функции распределения для выборки A
Вычислим суммы для среднего арифметического и дисперсии по формулам (2.6 и 2.9) и по вариационному ряду (см. таблицу 1).
Далее по формуле (2.6) вычисляем среднее арифметическое
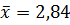
и по формуле (2.9) – дисперсию
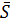 2 = 2,3668.
2 = 2,3668.
Стандартное (или среднеквадратичное) отклонение 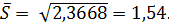 Вспомним, что
Вспомним, что 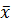 ,
, 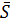 2 и
2 и 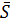 являются выборочными (приближёнными) оценками генеральных (истинных) значений характеристик EX(или
являются выборочными (приближёнными) оценками генеральных (истинных) значений характеристик EX(или 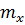 ), DX(или
), DX(или 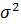 ) и
) и 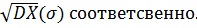 Модой Мо здесь является значение с максимальной частотой, то есть Мо = 3 (см. п. 2.1.5.4). Медиана Ме данного вариационного ряда: Ме = 3 (см. п. 2.1.5.5).
Модой Мо здесь является значение с максимальной частотой, то есть Мо = 3 (см. п. 2.1.5.4). Медиана Ме данного вариационного ряда: Ме = 3 (см. п. 2.1.5.5).
Задача 2.2
Имеется выборка B, её интервалы и частоты ni и т. д. (см. таблицу 2). Рассмотрим вариационный ряд по интервалам значений:
Таблица 2. Выборка B
| Интервалы | ni | относительные частоты ni/n | Накопленные относительные частоты |
| 59-63 | 0,015 | 0,015 | |
| 63-67 | 0,115 | 0,130 | |
| 67-71 | 0,335 | 0,465 | |
| 71-75 | 0,380 | 0,845 | |
| 75-79 | 0,135 | 0,980 | |
| 79-83 | 0,020 | 1,000 | |
| n =200 | 1,000 | - |
При построении графиков вариационного ряда откладываем по оси x значения с 61 по 81 и по оси ni/n – значения с 0.015 по 0,380 (рисунки 20,21).
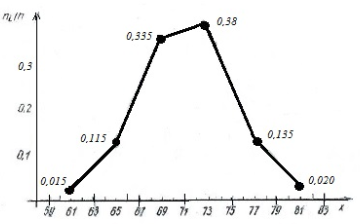
Рисунок 20. Полигон (частот) вариационного ряда выборки B
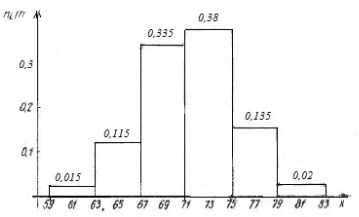
Рисунок 21. Гистограмма вариационного ряда выборки B
Далее учитываем, что в качестве представителя каждого интервала взят его конец. Принимая за координаты точек концы интервалов и соответствующие накопленные частоты (см. таблицу 2), соединяя эти точки прямыми линиями, построим график эмпирической функции распределения F(x) - рис.22.
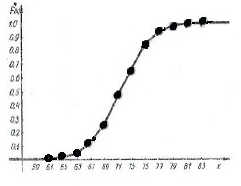
Рисунок 22. График эмпирической функции распределения F(x) выборки B
По формуле (2.6) вычисляем оценку среднего арифметического
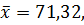
а по формуле (2.9) – оценку дисперсии
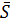 2 = 14,6176.
2 = 14,6176.
Оценка стандартного отклонения 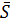 =
= 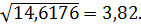
Моду находим по формуле (2.11):
Мо = 69 + 4 * 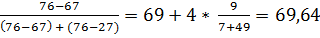 .
.
Медиану находим по формуле (2.12):
Ме = 71 + 4 * 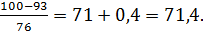
Дата добавления: 2018-11-26; просмотров: 1583;











