Статистические гипотезы
2.3.1 Понятие статистической гипотезы
Статистической гипотезой называется любое утверждение о виде или свойствах распределения, наблюдаемых в эксперименте случайных величин. Например, случайная величина Х имеет распределение Пуассона, случайная величина с нормальным распределением имеет среднее значение μ = 5 или μ ≠ 5 и т.д. Статистические гипотезы проверяются статическими методами, с помощью статистических критериев.
Гипотезы о неизвестном параметре θ распределения бывают простые и сложные; простая гипотезаутверждает, что параметр θ имеет одно конкретное значение (например, θ = 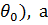 сложнаягипотеза утверждает, что параметр θ имеет значение из совокупности (интервала) значений (например, θ<
сложнаягипотеза утверждает, что параметр θ имеет значение из совокупности (интервала) значений (например, θ< 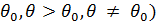 .
.
Основную (проверяемую) гипотезуобозначим 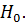 Обычно вырабатывают еще и альтернативную гипотезу
Обычно вырабатывают еще и альтернативную гипотезу 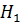 ,отрицающую или исключающую основную гипотезу
,отрицающую или исключающую основную гипотезу 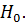 Таким образом, в результате проверки можно принимать только одну из гипотез
Таким образом, в результате проверки можно принимать только одну из гипотез 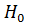 или
или 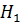 , отвергая в это же время другую.
, отвергая в это же время другую.
Гипотезу проверяют на основании выборки, полученной из генеральной совокупности. Из-за случайности и малого объема выборки в результате проверки могут возникать ошибки и приниматься неправильные решения. В принципе возможны два рода ошибок. Ошибка первого родаимеет место тогда, когда отвергается, будучи правильной, гипотеза 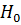 , а принимается неверная гипотеза
, а принимается неверная гипотеза 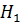 .При ошибке второго рода принимается неправильная гипотеза
.При ошибке второго рода принимается неправильная гипотеза 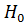 , хотя верна альтернативная
, хотя верна альтернативная 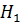 .
.
Таким образом, по одним выборкам принимается правильное решение, а по другим – неправильное. Решение принимается по искомому значению некоторой характеристики (функции) выборки, называемой статистикойили статистической характеристикой(это может быть, например, среднее значение). Множество значений этой статистики можно разделить на два непересекающихся подмножества:
¾ значения статистики, при которых гипотеза Н0 принимается (не отклоняется), называемые областью принятия гипотезы (допустимой областью), например, доверительный интервал;
¾ значения статистики, при которых гипотеза Н0 отвергается (отклоняется) и принимается гипотеза Н1,называемая критической областью (см. рис. 25), ей соответствуетвероятность, равная 𝛼.
Очевидно, что проверка гипотез выполняется при малой вероятности принятия неправильных решений.Допустимая вероятность ошибки первого рода обозначается через aи называется уровнем значимости 𝛼 = 1 - 𝛾. Значение 𝛼 обычно мало (0,1, …, 0,001). Но уменьшение вероятности ошибки первого рода обычно вызывает увеличение вероятности ошибки второго рода(b).
Статистика выбирается так, чтобы вероятности α и β были бы минимальными (методы выбора наилучшей статистики здесь не рассматриваются). Будем предполагать, что распределение статистики при правильной гипотезе Н0 известно.
Чтобы определить критическую область для статистики, используют уровень значимости α и учитывают вид альтернативной гипотезы Н1.Основная или нуль-гипотеза Н0 о значении неизвестного параметра q распределения обычно выглядит так:
Н0: q = q0.
Альтернативная гипотеза Н1 может при этом иметь один из следующих видов:
Н1: q < q0, Н1: q > q0 или Н1: q ¹ q0.
Соответственно этому можно получить левостороннюю, правостороннюю или двустороннюю критические области (рисунок 25). Граничные точки критических областей определяют по таблицам распределения статистики (считаем распределение известным), используя значения (квантили), отвечающие уровню доверительной вероятности γ (или уровню значимости α = 1- γ).
Проверка статистической гипотезы состоит из следующих этапов:
1) определение (выбор) гипотез Н0 и Н1;
2) выбор статистической характеристики (статистики) и задание уровня значимости α;
3) определение границ критической области (по таблицам, по уровню значимости α и по альтернативной гипотезе Н1);
4) вычисление по выборке значения статистики (искомой статистической характеристики);
5) сравнение значения статистики с границей критической области;
6) принятие решения (гипотезы): если значение статистики не попадает в критическую область (см. рис. 25), то принимается нуль-гипотеза Н0 и отвергается альтернативная гипотеза H1 (здесь возможна ошибка второго рода), а если попадает в критическую область, то отвергается гипотеза Н0 и принимается гипотеза Н1(в этом случае возможна ошибка первого рода).
допустимые области
α α α/2 α/2
k k k1 k2
| б) |
| в) |
| а) |
Рисунок 25. Критические области:
а – левосторонняя, б – правосторонняя, в – двусторонняя
Иногда целесообразно перед определением альтернативной гипотезы H1 выполнить этап 4, где для получения значения статистики нужно вычислить несмещённые оценки параметров генеральной совокупности. Например, если проверяется нуль-гипотеза Н0: 𝜇 ≠ 5 и несмещенная оценка среднего значения 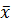 = 7,2, т.е.
= 7,2, т.е. 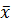 >𝜇, то имеют смысл только следующие альтернативные гипотезы Н1: 𝜇 > 5 или Н1: 𝜇 = 5.
>𝜇, то имеют смысл только следующие альтернативные гипотезы Н1: 𝜇 > 5 или Н1: 𝜇 = 5.
Результаты проверки статистической гипотезы нужно интерпретировать так: если мы приняли альтернативную гипотезу Н1, то можно считать ее доказанной, а если приняли основную гипотезу Н0, то мы признали лишь, что гипотеза Н0 при заданном уровне значимости α не противоречит результатам наблюдений. Однако этим свойством наряду с Н0 могут обладать и другие гипотезы. Например, если мы принимаем гипотезу Н0: 𝜇 = 5, то может случиться, что по данной выборке можно, при заданном α, принять и другие гипотезы, например, Н0: 𝜇 = 5,5 или Н0:
𝜇 = 4 и т.д. Вопрос о том, как найти среди них наилучшую гипотезу, здесь не рассматриваем. Следует помнить, что, принимая гипотезу Н0, для надежности надо проводить еще дополнительные (дальнейшие) исследования.
2.3.2 Гипотеза о среднем значении нормального распределения при известном σ
Предполагаем, что генеральная совокупность имеет нормальноераспределение X ∈ N (μ, σ), причём значение σ известно.При уровне значимости a нужно проверить нуль-гипотезу Н0: 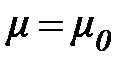 (например, µ0 = 5). В качестве альтернативной можно использовать одну из следующих гипотез Н1:
(например, µ0 = 5). В качестве альтернативной можно использовать одну из следующих гипотез Н1: 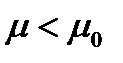 , Н1:
, Н1: 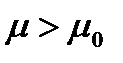 или Н1:
или Н1: 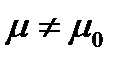 . В качестве статистики (статистической характеристики) воспользуемся нормированной (безразмерной) случайной величиной
. В качестве статистики (статистической характеристики) воспользуемся нормированной (безразмерной) случайной величиной
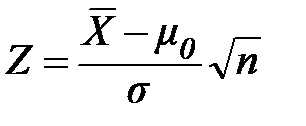 ,(2.35)
,(2.35)
где 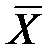 - неизвестное генеральное среднее значение,
- неизвестное генеральное среднее значение,
которая при истинной гипотезе Н0 имеет нормированное нормальное распределение Z ∈ N(0, 1)(см. п. 1.2.8, формулы 1.43 … 1.44).
Критическую область определяем с помощью таблицы функции распределения (см. приложение 3) Ф(х) нормального распределения (x>0).
Если альтернативная гипотеза имеет вид Н1: 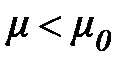 , то используем левостороннюю критическую область, которая удовлетворяет (рисунок 26) следующему условию:
, то используем левостороннюю критическую область, которая удовлетворяет (рисунок 26) следующему условию:
P(Z < - 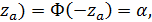 (2.36)
(2.36)
где аргумент 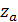 - квантиль нормированного N-распределения (из приложения 3 для х = z). Вспомним, что
- квантиль нормированного N-распределения (из приложения 3 для х = z). Вспомним, что 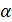 - это вероятность попадания значения статистической характеристики (здесь z) в критическую область.
- это вероятность попадания значения статистической характеристики (здесь z) в критическую область.
Таблицы составлены только для положительных значений аргумента (Z>0), поэтому из таблицы найдем 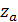 , учитывая [см. формулу (1.17)], что
, учитывая [см. формулу (1.17)], что
Ф( 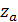 ) = 1 –
) = 1 – 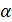 . (2.37)
. (2.37)
Отсюда следует, что критическая область (здесь - левосторонняя) – это множество таких Z, для которых
Z<- 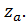 (2.38)
(2.38)
f(z) f(z)
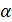
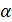
- 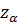 0 z 0
0 z 0 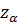 z крит. обл. z допуст. обл. z допуст. обл. z крит. обл. z
z крит. обл. z допуст. обл. z допуст. обл. z крит. обл. z
Рисунок 26. Левосторонняя Рисунок 27. Правосторонняя
критическая область критическая область
Если альтернативная гипотеза имеет вид 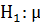 >
> 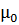 , то используем правостороннюю критическую область, которая удовлетворяет (рисунок 27) условию
, то используем правостороннюю критическую область, которая удовлетворяет (рисунок 27) условию
Р(Z > 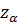 ) = α. (2.39)
) = α. (2.39)
Из таблицы получаем значение 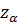 , учитывая, что (см. 2.37) здесь
, учитывая, что (см. 2.37) здесь
Р(Z < 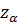 ) = Ф(
) = Ф( 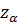 ) = 1 – α. (2.40)
) = 1 – α. (2.40)
Отсюда находим правостороннюю критическую область
Z > 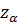 . (2.41)
. (2.41)
И наконец, при альтернативной гипотезе 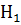 : µ ≠
: µ ≠ 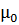 используем двухстороннюю (симметричную) критическую область, удовлетворяющую (рис. 28) условию
используем двухстороннюю (симметричную) критическую область, удовлетворяющую (рис. 28) условию
Р(|Z| > 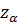 ) = α.(2.42)
) = α.(2.42)
f (z)
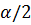
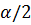
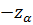 0
0 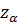 z
z
Рисунок 28. Двусторонняя критическая область
Учитывая определение абсолютной величины, находим вероятность попадания в левостороннюю и правостороннюю критические подобласти (в каждую по отдельности):
Р(Z < 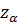 ) = Р(Z >
) = Р(Z > 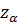 ) = α/2.
) = α/2.
По формуле (2.39) и (2.40) получаем условие для использования
таблицы при нахождении 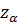 :
:
Ф( 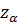 ) = 1 - α/2.(2.43)
) = 1 - α/2.(2.43)
Таким образом, двусторонняя (симметричная) критическая область имеет вид
|Z| > 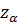 , т. е. Z < -
, т. е. Z < - 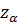 и Z >
и Z > 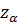 . (2.44)
. (2.44)
Для вычисления значения статистики Z c помощью формулы (2.35) нужно по выборке найти среднее арифметическое 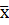 .
.
Задача 2.6
При уровне значимости α = 0,01, проверить одностороннюю гипотезу о среднем: H0: µ = 65 при альтернативе H1: µ > 65, при заданном σ = 5,5; 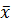 = 68,1, n = 20.
= 68,1, n = 20.
Статистика Z [см. формулу (2.35)] имеет нормальное распределение.
Решение:По альтернативной гипотезе H1 найдём правостороннюю критическую область [см. (2.40)].
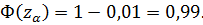
По таблицам нормального распределения (см. приложение 3) получаем 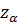 = 2,33. Отсюда следует, что критическая область имеет вид
= 2,33. Отсюда следует, что критическая область имеет вид
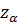 > 2,33. Вычислим значение статистики по формуле (2.35):
> 2,33. Вычислим значение статистики по формуле (2.35):
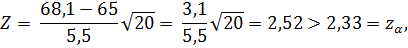
то есть значение статистики (статистической характеристики Z) принадлежит критической области:
допустимая обл. крит. обл.
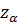 = 2,33 2,52
= 2,33 2,52
Следовательно, отвергаем гипотезу H0 и принимаем гипотезу H1: µ > 65.
2.3.3 Гипотеза о среднем значении нормального распределения при неизвестном σ
Предположения те же, что и в предыдущем пункте, но только σнеизвестно. В этом случае в качестве статистики используют тоже нормированную случайную величину
t = 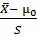
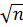 , (2.45)
, (2.45)
которая, если верна гипотеза 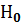 , имеетt – распределение (Стьюдента) с числом степеней свободы f = n – 1, где n – объем выборки.
, имеетt – распределение (Стьюдента) с числом степеней свободы f = n – 1, где n – объем выборки.
Критические области определяются так же, как и в предыдущем пункте. Но использование таблицы t – распределения Стьюдента проще, так как она составлена именно для определения критических областей (через α и f). При нахождении левосторонней или правосторонней критических областейиспользуем верхнюю (головку, шапку) таблицы, а для двусторонней – нижнюю.
Перед вычислением по формуле (2.45) значения статистики (статистическая характеристика) t нужно по выборке вычислить 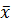 и S.
и S.
Задача 2.7
При уровне значимости α = 0,1, проверить (одностороннюю) гипотезу о среднем: H0: µ = -264 при альтернативе H1: µ < -264.
Решение: по выборке найдено: 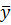 = -267,45;
= -267,45; 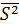 = 485,65 при n = 20 (объём выборки), то есть f = n – 1 = 19. По формуле (2.14) вычисляем несмещённую оценку дисперсии S2 = (20/19)*485,65 = 511,21, отсюда несмещенная оценка с.к.о. S = 22,6.
= 485,65 при n = 20 (объём выборки), то есть f = n – 1 = 19. По формуле (2.14) вычисляем несмещённую оценку дисперсии S2 = (20/19)*485,65 = 511,21, отсюда несмещенная оценка с.к.о. S = 22,6.
Статистика t [см. (2.45)] имеет t – распределение (Стьюдента) с числом степеней свободы f = n – 1. При альтернативной гипотезе H1 найдём левостороннюю критическую область по условию P(t < tα) = 0,1. Из таблицы t – распределения (Стьюдента) (см. приложение 5) получаем tα = -1,33. Отсюда критическая область t < -1,33. Значение статистики вычислим по формуле (2.45):
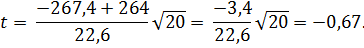
Значение статистики не принадлежит критической области и нет оснований отвергать (то есть принимаем) основную гипотезу H0: µ = -264:
критическая обл. допустимая обл.
tα = -1,33 -0,67
2.3.4 Гипотеза о дисперсии нормального распределения
Предполагаем, что генеральная совокупность имеет нормальноераспределение Х є N (µ, σ), где параметр σ неизвестен. Требуется при уровне значимости α проверить нуль – гипотезу 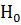 о генеральной дисперсии:
о генеральной дисперсии:
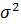 =
= 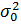 (конкретное число, например, 9,5). В качестве статистики используем случайную величину
(конкретное число, например, 9,5). В качестве статистики используем случайную величину
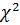 =
= 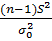 , (2.46)
, (2.46)
где  – несмещённая выборочная дисперсия(2.14).
– несмещённая выборочная дисперсия(2.14).
Если гипотеза 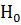 верна, то случайная величина
верна, то случайная величина 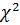 имеет
имеет
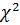 –распределение (Пирсона) с числом степеней свободы f = n – 1,
–распределение (Пирсона) с числом степеней свободы f = n – 1,
гдеn – объём выборки.
Критическая область определяется в зависимости от альтернативной гипотезы 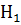 по таблице
по таблице 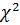 – распределения (см. приложение 4).
– распределения (см. приложение 4).
Если альтернативная гипотеза имеет вид 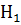 :
: 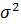 <
< 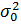 , то используем левостороннюю критическую область, удовлетворяющую условию
, то используем левостороннюю критическую область, удовлетворяющую условию
Р( 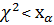 ) = α, (2.47)
) = α, (2.47)
где α – уровень значимости ( это вероятность попадания в критическую область - вероятность ошибки 1 рода).
Таблица 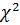 - распределения составлена в соответствии с противоположным условием
- распределения составлена в соответствии с противоположным условием 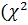 >
> 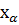 ) и, значит, для нахождения из таблицы значения
) и, значит, для нахождения из таблицы значения 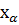 используем условие
используем условие
Р 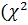 >
> 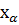 ) = 1 – α, (2.48)
) = 1 – α, (2.48)
где(1 – α)- это вероятность попадания в допустимую область.
При альтернативной гипотезе 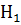 :
: 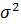 >
> 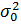 находим правостороннюю критическую область, исходя из условия
находим правостороннюю критическую область, исходя из условия
Р 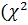 >
> 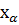 ) = α, (2.49)
) = α, (2.49)
по которому 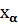 можно найти непосредственно из таблицы (приложение 4).
можно найти непосредственно из таблицы (приложение 4).
При альтернативной гипотезе 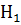 :
: 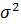 ≠
≠ 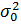 находим двустороннюю критическую область (точнее две подобласти) согласно условию
находим двустороннюю критическую область (точнее две подобласти) согласно условию
Р(( 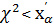 ), а также и (
), а также и ( 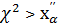 )) = α(2.50)
)) = α(2.50)
в общей сложности для двух подобластей, где 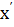 и
и 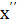 - критические (граничные) значения..
- критические (граничные) значения..
Обычно принимают симметричную по вероятности критическую область, удовлетворяющую условию
Р( 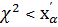 ) = Р(
) = Р( 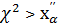 ) = α/2, (2.51)
) = α/2, (2.51)
подобно рисунку 28.
Для этого условия из таблицы квантилей распределения Пирсона (приложение 4) можно сразу найти 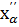 , а для получения
, а для получения 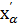 следует преобразовать условия (2.47) и (2.48) к виду
следует преобразовать условия (2.47) и (2.48) к виду
Р 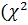 >
> 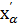 ) = 1 - α/2. (2.52)
) = 1 - α/2. (2.52)
По выборке нужно вычислить несмещенную оценку дисперсии генеральной совокупности 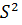 по формуле (2.14), а затем по формуле (2.46) найти значение статистики
по формуле (2.14), а затем по формуле (2.46) найти значение статистики 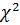 для проверки гипотезы.
для проверки гипотезы.
Задача 2.8
При уровне значимости α = 0,01, проверить (одностороннюю) гипотезу о дисперсии: H0: 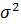 =
= 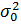 = 1876 при альтернативе H1:
= 1876 при альтернативе H1: 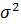 > 1876.
> 1876.
Решение. По выборке найдена дисперсия 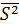 = 1786,89 при n = 20; число степеней свободы f = n - 1 = 19.
= 1786,89 при n = 20; число степеней свободы f = n - 1 = 19.
Вычисляем несмещенную оценку дисперсии S2 = (20/19)*1786,89 = 1880,94, отсюда оценка с.к.о. S = 43, 4.
Статистика 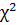 [см. (2.46)] имеет
[см. (2.46)] имеет 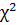 – распределение с числом степеней свободы n-1. По альтернативной гипотезе H1 найдём правостороннюю критическую область, используя условие (2.49) и таблицу
– распределение с числом степеней свободы n-1. По альтернативной гипотезе H1 найдём правостороннюю критическую область, используя условие (2.49) и таблицу
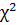 – распределения (Пирсона) (см. приложение 4).
– распределения (Пирсона) (см. приложение 4).
Находим по таблице квантиль распределения Пирсона xα (границу критической области, где H0 не верна) при 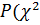 > xα) = α = 0,01, критическое значение из таблицы xα = 36,191,
> xα) = α = 0,01, критическое значение из таблицы xα = 36,191, 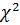 > 36,191.
> 36,191.
По формуле (2.46) вычислим значение статистики:
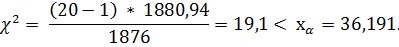
Это значение не принадлежит критической области, поэтому нуль-гипотеза H0: 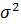 = 1876 не будет отвергнута (принимается):
= 1876 не будет отвергнута (принимается):
допустимаяобласть критическая обл.
19,1 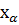 = 36,191
= 36,191
2.3.5 Гипотеза о равенстве двух средних значений
Предполагаем, что имеются две генеральные совокупности с нормальным распределением Х1 є N (µ1, σ1), Х2 є N (µ2, σ2), при этом истинные (генеральные) стандартные отклонения σ1 и σ2неизвестны, но должны быть равными (однородными, близкими). Поэтому на практике, до проверки равенства двух средних значений сначала всегда нужно проверить гипотезу о равенстве дисперсий. Из обеих генеральных совокупностей сделано по одной независимой выборке с параметрами 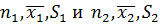 соответственно.
соответственно.
Полагая дисперсии однородными, т.е. 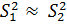 , обозначим разность средних значений для этих двух N – распределений через
, обозначим разность средних значений для этих двух N – распределений через 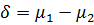 . Зафиксировав уровень значимости α, проверим нуль-гипотезу H0:
. Зафиксировав уровень значимости α, проверим нуль-гипотезу H0: 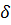 =
= 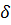 0 (некоторое конкретное число), используя статистику
0 (некоторое конкретное число), используя статистику
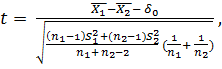 (2.53)
(2.53)
где величина приведённой дисперсии (средневзвешенной по степеням свободы) 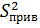 =
= 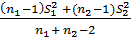 ,
, 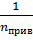 =
= 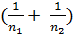 – это среднее гармоническое из n1 и n2 для определения приведенного nприв.
– это среднее гармоническое из n1 и n2 для определения приведенного nприв.
Если гипотеза H0 верна, то случайная величина t имеет t – распределение (Стьюдента) с числом степеней свободы f = 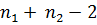 . Обычно берут
. Обычно берут 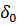 = 0, то есть проверяется гипотеза о равенстве (однородности) средних значений генеральных совокупностей H0:
= 0, то есть проверяется гипотеза о равенстве (однородности) средних значений генеральных совокупностей H0: 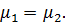
В общем случае критическая область определяется в зависимости от вида альтернативной гипотезы H1 :
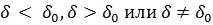
(последняя является двусторонней гипотезой) по таблице t – распределения (см. приложение 5 для tα,f).
Задача 2.9
При уровне значимости α = 0,001, проверить гипотезу о равенстве (близости) средних значений µ1 и µ2для двух выборок:
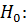
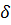 = µ1 - µ2 =
= µ1 - µ2 = 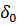 = 0 при альтернативе H1:
= 0 при альтернативе H1: 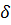 < 0 (µ1 < µ2).
< 0 (µ1 < µ2).
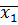 = -34,2,
= -34,2, 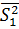 = 69, 14, n1 = 6,
= 69, 14, n1 = 6, 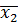 = -30,5,
= -30,5, 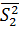 = 70, 58, n2 = 6.
= 70, 58, n2 = 6.
Решение:Найдем 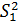 = (6/5)*69,14 = 82,97 и
= (6/5)*69,14 = 82,97 и 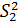 = (6/5)*70,58 = 84,70.
= (6/5)*70,58 = 84,70.
Статистика t [см. (2.53)] имеет t-распределение с числом степеней свободы f = n1 + n2 – 2. По альтернативной гипотезе H1, используя условие P(t < tα) = 0,001 и таблицу t-распределения (Стьюдента) (см. приложение 5), найдём левостороннюю критическую область
tα = -4,14, t < -4,14.
Не проверяя здесь, как требуется при сравнении средних двух выборок, прежде равенство их дисперсий (с тем же α), проверим сразу равенство средних µ1 и µ2 .По формуле (2.53) вычислим значение статистики
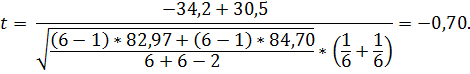
Это значение > -4,14, следовательно не принадлежит критической области, поэтому оснований отвергать нуль-гипотезу 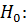
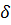 = 0 нет, таким образом средние значения µ1 и µ2 генеральных совокупностей однородными (равными). При этом ещё раз вспомним, что здесь мы без проверки предполагали, что дисперсии генеральных совокупностей равны (однородны, близки)
= 0 нет, таким образом средние значения µ1 и µ2 генеральных совокупностей однородными (равными). При этом ещё раз вспомним, что здесь мы без проверки предполагали, что дисперсии генеральных совокупностей равны (однородны, близки) 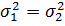 .
.
критическая обл. допустимая обл.
tα = -4,14 -0,70
2.3.6 Гипотеза о равенстве двух дисперсий
Предполагаем, как и в предыдущем пункте, что заданы две генеральные совокупности X1 и X2 c нормальным распределением: Х1 є N (µ1, σ1), Х2 є N (µ2, σ2). Из этих генеральных совокупностей сделаны независимые выборки с параметрами > 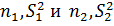 соответственно. Требуется при уровне значимости α проверить нуль – гипотезу H0: s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
соответственно. Требуется при уровне значимости α проверить нуль – гипотезу H0: s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 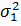 =
= 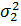 о равенстве (однородности) дисперсии при альтернативной гипотезе H1: s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
о равенстве (однородности) дисперсии при альтернативной гипотезе H1: s w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSubSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 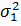 >
> 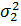 . Обычно здесь другие альтернативные гипотезы не используют.
. Обычно здесь другие альтернативные гипотезы не используют.
Для определенности, предполагая, что 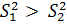 , принимаем в качестве статистики величину дисперсионного отношения
, принимаем в качестве статистики величину дисперсионного отношения
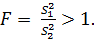 (2.54)
(2.54)
Если гипотеза H0 верна, то случайная величина F имеет
F – распределение (Фишера) с числами степеней свободы f1 = n1 – 1 и f2 = n2 – 1 для числителя и знаменателя соответственно. Критическая область будет только правосторонняя и определяется условием
P(F > Fα )= α. (2.55)
Критическое значение Fα найдём из таблиц F – распределения (см. приложение 6 для Fα , f1, f2). Значения Fα зависят от трёх величин: уровня значимости α и двух чисел степеней свободы f1 и f2, поэтому таблицы составлены отдельно от каждого значения α (трёхмерные таблицы, то есть таблицы с тремя входами). В таблицах число степеней свободы большей дисперсии f1 (для числителя, см. (2.54)) расположено в верхней части таблицы, f2 – с левой стороны.
Задача 2.10
Проверка гипотезы о равенстве двух дисперсий а также полная проверка однородности двух выборок при уровне значимости α = 0,01, имеющих следующие основные числовые характеристики: 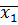 = 68,1;
= 68,1; 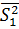 = 30, 2; n1 = 20;
= 30, 2; n1 = 20; 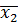 = 67,6;
= 67,6; 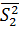 = 29, 2; n2 = 20.
= 29, 2; n2 = 20.
Решение:сначала проверяем гипотезу о равенстве дисперсий. Рассмотрим основную гипотезу 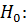
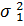 =
= 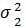 при альтернативе H1:
при альтернативе H1: 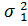 >
> 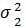 .
.
Получаем следующую (правостороннюю) критическую область:
P(F > Fα) = 0,01, Fα = 2,92 - табличное значение квантиля F-распределения (Фишера).
Надо проверить альтернативную гипотезу H1, то есть F > 2,92.
Вычислим значение статистики (формула 2.54), так называемое дисперсионное отношение
F = 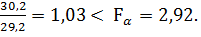
Оно не принадлежит критической области, поэтому принимаем нуль-гипотезу H0 о равенстве дисперсий (в противном случае проверка однородности выборок уже бы закончилась с отрицательным результатом). Следовательно, теперь стоит проверить и гипотезу о равенстве средних значений генеральных совокупностей.
Надо при α = 0,01 проверить: H0: 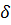 = 0, то есть µ1 = µ2,
= 0, то есть µ1 = µ2,
при H1 : 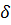 > 0 (µ1 > µ2).
> 0 (µ1 > µ2).
Получаем следующую критическую область: P(t > tα) = 0,01, по таблице приложения 5 находим tα = 2,42, т. е. t > 2,42 для гипотезы 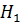 (правосторонняя критическая область).
(правосторонняя критическая область).
Вычисляем значение статистики
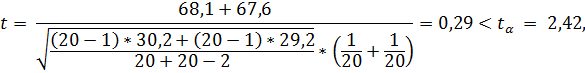
то есть оно не принадлежит критической области, поэтому принимаем основную гипотезу 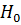 о равенстве средних значений. Таким образом, рассмотренные выборки однородны, их можно объединить и найти общие
о равенстве средних значений. Таким образом, рассмотренные выборки однородны, их можно объединить и найти общие 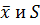 для такой выборки объёмом n =
для такой выборки объёмом n = 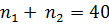 .
.
допустимая обл.критическая обл.
0,29 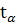 = 2,92
= 2,92
2.3.7 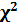 – критерий согласия
– критерий согласия
Рассмотрим, как можно проверить гипотезу о распределении генеральной совокупности X. Пусть генеральная совокупность имеет какое-то неизвестное распределение. Сделаем выборку из генеральной совокупности. На основании выборки, или учитывая какие-то другие соображения, составим гипотезу о конкретном виде распределения генеральной совокупности, выраженной через функцию распределения F(x). Это распределение назовём теоретическим (ожидаемым, предполагаемым).
По выборке можем найти эмпирическую функцию распределения F*(x). Гипотеза H0 о распределении генеральной совокупности принимается тогда, когда эмпирическое распределение хорошо согласуется с теоретическим. Полного совпадения, конечно, ожидать не стоит. Для проверки таких гипотез разработаны несколько критериев согласия. Мы рассмотрим только 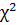 – критерий согласия (Пирсона).
– критерий согласия (Пирсона).
При использовании 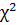 – критерия согласия вся область значений генеральной совокупности X делится на k интервалов, которые могут иметь различную длину. Крайние интервалы могут иметь вид r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">
– критерия согласия вся область значений генеральной совокупности X делится на k интервалов, которые могут иметь различную длину. Крайние интервалы могут иметь вид r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 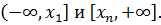 По выборке составляют вариационный ряд по этим же интервалам. Если в некотором интервале эмпирическая (фактическая) частота ni слишком мала (ni меньше 5), то этот интервал объединяют с соседним интервалом. При дискретной генеральной совокупности интервал может содержать только одно значение генеральной совокупности. Построенная по частотам ni гистограмма или другие соображения (гипотезы) позволяют выбрать теоретическое (ожидаемое) распределение.
По выборке составляют вариационный ряд по этим же интервалам. Если в некотором интервале эмпирическая (фактическая) частота ni слишком мала (ni меньше 5), то этот интервал объединяют с соседним интервалом. При дискретной генеральной совокупности интервал может содержать только одно значение генеральной совокупности. Построенная по частотам ni гистограмма или другие соображения (гипотезы) позволяют выбрать теоретическое (ожидаемое) распределение.
По выборке вычисляют оценки параметров теоретического, предполагаемого распределения. Тем самым теоретическое распределение будет полностью определено. Теперь по теоретическому распределению вычислим вероятности pi того, что случайная величина X принимает значение из i-го интервала, при этом 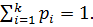 Затем найдём теоретические частоты mi = n * pi , здесь n – объём выборки.
Затем найдём теоретические частоты mi = n * pi , здесь n – объём выборки.
Гипотеза H0 о близости эмпирического и теоретического распределений верна, если теоретические и эмпирические частоты mi и ni достаточно мало отличаются друг от друга. Для проверки этого, то есть гипотезы H0, используем следующую статистику (статистическую характеристику):
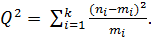 (2.56)
(2.56)
Случайная величина 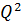 имеет
имеет 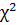 – распределение (Пирсона) с числом степеней свободы f = k – r – 1, где k – количество интервалов, r – количество параметров теоретического распределения, оценки которых вычислялись по рассматриваемой выборке. Например, если ожидаем N-распределение и определяем
– распределение (Пирсона) с числом степеней свободы f = k – r – 1, где k – количество интервалов, r – количество параметров теоретического распределения, оценки которых вычислялись по рассматриваемой выборке. Например, если ожидаем N-распределение и определяем 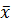 и S, то следовательно r = 2.
и S, то следовательно r = 2.
Чем больше 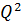 , тем хуже согласованы теоретическое и эмпирическое распределения (велико различие эмпирических и теоретических частот). При достаточно большом значении
, тем хуже согласованы теоретическое и эмпирическое распределения (велико различие эмпирических и теоретических частот). При достаточно большом значении 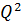 (больше критического по таблице
(больше критического по таблице 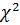 – критерия согласия, см. приложение 4) гипотезу H0 нужно отвергнуть. Поэтому используем только правостороннюю критическую область, где
– критерия согласия, см. приложение 4) гипотезу H0 нужно отвергнуть. Поэтому используем только правостороннюю критическую область, где 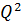 >
> 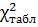 (рис. 25, б), а гипотеза H0 – не верна.
(рис. 25, б), а гипотеза H0 – не верна.
При 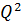 <
< 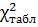 , попадаем в допустимую область, где верна нуль-гипотеза H0 о близости (хорошей согласованности) эмпирического (фактического) и теоретического (ожидаемого) распределений.
, попадаем в допустимую область, где верна нуль-гипотеза H0 о близости (хорошей согласованности) эмпирического (фактического) и теоретического (ожидаемого) распределений.
Задача 2.11
В двух филиалах ВУЗа за семестр, соответственно по курсам, было за неуспеваемость отчислено следующее количество студентов, при одинаковом общем количестве отчисленных в филиалах, (таблица 4):
Таблица 4
| курс | 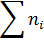
| |||||
| филиал 1 | ||||||
| филиал 2 |
При α = 0,10 проверить (сравнить) однородность, близость распределения по курсам отчисленных студентов в филиалах.
Решение:Воспользуемся для сравнения критерием Пирсона, здесь 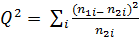 . Нуль-гипотеза H0: распределения n1 и n2 – однородны при α = 0,10. Из таблицы видно, что на 4-м и 5-м курсах количество n1 и n2 меньше 5-ти, следовательно, надо объединить значения для двух последних колонок (курсов) в одну четвертую группу, то есть получим здесь соответственно: n1,4 = 3 + 3 = 6 и n2,4 = 5 + 2 = 7.
. Нуль-гипотеза H0: распределения n1 и n2 – однородны при α = 0,10. Из таблицы видно, что на 4-м и 5-м курсах количество n1 и n2 меньше 5-ти, следовательно, надо объединить значения для двух последних колонок (курсов) в одну четвертую группу, то есть получим здесь соответственно: n1,4 = 3 + 3 = 6 и n2,4 = 5 + 2 = 7.
Находим Q2 = 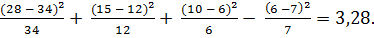
Число степеней свободы (с учётом объединения колонок) f = m - 1 = 4 – 1 = 3. Критическое значение (квантиль из таблицы
Дата добавления: 2018-11-26; просмотров: 915;











