Теория выборочных оценок
2.2.1 Понятие оценки
Генеральные совокупности характеризуются некоторыми постоянными, истинными числовыми характеристиками (распределения). По выборкам можно найти оценки этих характеристик. Вследствие случайности выборок значения оценок одной и той же числовой характеристики, вычисленныепо разным выборкам из одной и той же генеральной совокупности, бывают, как правило, различными.
Обозначим неизвестный параметр распределения, то есть числовую характеристику генеральной совокупности X, через q , а оценку этого неизвестного параметра через 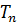 . Оценка
. Оценка 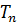 –это функция от выборки. Оценки неизвестного параметра можно находить различными способами. Например, если нужнооценить среднее значение q = µ нормального распределения, то можно использовать следующие оценки
–это функция от выборки. Оценки неизвестного параметра можно находить различными способами. Например, если нужнооценить среднее значение q = µ нормального распределения, то можно использовать следующие оценки 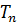 :
:
1) 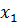 – единственный элемент выборки. На практике часто так и поступают: измеряют какую-то величину только один раз и этот результат используют как оценку среднего значения;
– единственный элемент выборки. На практике часто так и поступают: измеряют какую-то величину только один раз и этот результат используют как оценку среднего значения;
2) 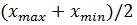 - среднее арифметическое максимального и минимального элементов выборки;
- среднее арифметическое максимального и минимального элементов выборки;
3) 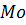 – мода, которая при нормальном распределении равна среднему значению μ;
– мода, которая при нормальном распределении равна среднему значению μ;
4) Me – медиана, которая при нормальном распределении также равна среднему значению μ (для малых выборок даёт неплохой результат);
5) 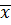 – среднее арифметическое.
– среднее арифметическое.
Для того чтобы установить, какая из оценок лучше, надо знать основныесвойства (виды) оценок.
2.2.2 Несмещенные оценки
Несмещенной называется оценка t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>, </m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 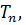 среднее значение которой равно оцениваемому параметру θ:
среднее значение которой равно оцениваемому параметру θ:
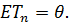
Если это условие не выполняется, то оценку называют смещенной, при этом смещение вычисляется как разность 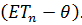
Несмещенной оценкой среднего значения μ является среднее арифметическое 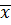 по выборке.
по выборке.
Аналогично с помощью выборочной дисперсии 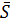 2 (см. (2.8)) можно оценить генеральную дисперсию
2 (см. (2.8)) можно оценить генеральную дисперсию 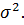 Оказывается, что выборочная дисперсия
Оказывается, что выборочная дисперсия 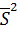 является смещённой оценкой дисперсии
является смещённой оценкой дисперсии 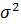 :
:
E 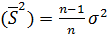 ,
,
то есть смещение (разность) 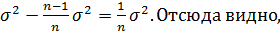 что при n → ∞ смещение стремится к нулю. Значит, при достаточно большом объеме выборки nвыборочную дисперсию можно приближенно принимать за несмещенную оценку дисперсии
что при n → ∞ смещение стремится к нулю. Значит, при достаточно большом объеме выборки nвыборочную дисперсию можно приближенно принимать за несмещенную оценку дисперсии 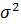 . Для оценки дисперсии, несмещенной при малом объеме выборки, используютисправленную дисперсию (с учетом смещения):
. Для оценки дисперсии, несмещенной при малом объеме выборки, используютисправленную дисперсию (с учетом смещения):
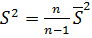 , (2.13)
, (2.13)
где (n-1)=fназывают числом степеней свободы при оценке параметра (здесь одна степень свободы из общего числа n – количества опытов “истрачена” на нахождение 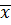 по формуле, связи (2.5)).
по формуле, связи (2.5)).
Если сравнить эту формулу с формулой для выборочной дисперсии из пункта 2.1.5.2 [см. формулы (2.8) – (2.9)], то можно получить аналогичные формулы для вычисления несмещенной оценки  дисперсии
дисперсии 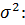
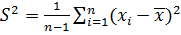 ; (2.14)
; (2.14)
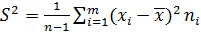 . (2.15)
. (2.15)
Задача 2.3
Используя выборку C (таблица 3), вычислить несмещённые оценки среднего значения µ, дисперсии σ2 и стандартного отклонения σ генеральной совокупности: 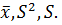
Несмещённую оценку среднего значения 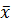 вычислим по формуле (2.5), несмещённые оценки дисперсии S2 формуле (2.14) и стандартного отклонения S по формуле S =
вычислим по формуле (2.5), несмещённые оценки дисперсии S2 формуле (2.14) и стандартного отклонения S по формуле S = 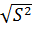 . Вычисления оформляем в таблицу 3.
. Вычисления оформляем в таблицу 3.
Таблица 3. Выборка C
| xi | xi- 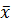
| (xi- 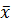 )2 )2
|
| -35 | -5,8 | 33,64 |
| -32 | -2,8 | 7,84 |
| -26 | 3,2 | 10,24 |
| -35 | -5,8 | 33,64 |
| -30 | -0,8 | 0,64 |
| -17 | 12,2 | 148,84 |
| -175 | - | 234,84 |
Имеем:
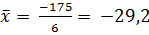 ;
;
S2 =  = 46,968;
= 46,968;
S = 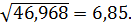
2.2.3 Доверительный интервал
Оценки 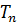 неизвестного параметра θ, рассмотренные выше, называют точечными, так как они определяют одно значение, одну точку на числовой оси. Все точечные оценки параметров распределения генеральной совокупности вычисляют по выборкам, но из-за случайности выборок оценки также являются случайными величинами, отличающимися от постоянного истинного значения параметра θ. Обозначим точность оценки через
неизвестного параметра θ, рассмотренные выше, называют точечными, так как они определяют одно значение, одну точку на числовой оси. Все точечные оценки параметров распределения генеральной совокупности вычисляют по выборкам, но из-за случайности выборок оценки также являются случайными величинами, отличающимися от постоянного истинного значения параметра θ. Обозначим точность оценки через 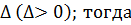 |
|  |
| 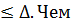 меньше
меньше  (односторонний доверительный интервал или полуинтервал неопределенности), тем точнее оценка.
(односторонний доверительный интервал или полуинтервал неопределенности), тем точнее оценка.
Любую точность можно получить с определенной вероятностью (надежностью) γ :
P(|  |≤ ∆)= γ(2.16)
|≤ ∆)= γ(2.16)
Если преобразовать это выражение, то можно переписать
P( 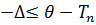 ≤ ∆)= γ
≤ ∆)= γ
или
P( 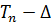 ≤
≤ 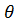 ≤
≤ 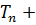 ∆)= γ (2.17)
∆)= γ (2.17)
Условие (2.17) означает, что интервал | 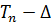 ,
, 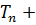 ∆| покрывает(т.е. включает в себя) значение генерального параметра
∆| покрывает(т.е. включает в себя) значение генерального параметра 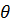 с заданной доверительной вероятностью
с заданной доверительной вероятностью 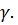 Точность оценки
Точность оценки  фактически определяет длину доверительного (двухстороннего, симметричного) интервала (2
фактически определяет длину доверительного (двухстороннего, симметричного) интервала (2 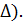
Доверительная вероятность 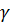 задается обычно значением, близким к единице, например, 0,90; 0,95; 0,98; 0,99 и т. д. Дополнительная (до 1) к ней величина α=1-γ называется уровнем значимости.
задается обычно значением, близким к единице, например, 0,90; 0,95; 0,98; 0,99 и т. д. Дополнительная (до 1) к ней величина α=1-γ называется уровнем значимости.
Доверительная вероятность γ, точность оценки ∆ и объем выборки n связаны между собой. Если определены две величины из них, то тем самым будет определена и третья.
2.2.4 Доверительный интервал для среднего значения μ нормального распределения при известном σ
Пусть задана генеральная совокупность с нормальным распределением X ∈ N (μ, σ), для которой генеральное значение стандартного отклонения σ известно. Для оценки параметра μ воспользуемсявеличиной 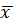 . Заметим, что и среднее арифметическое
. Заметим, что и среднее арифметическое 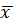 , и элементы выборки
, и элементы выборки 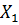 ,
,  из-за случайности выборок являются случайными величинами. Все элементы выборки имеют то же распределение, что и генеральная совокупность:
из-за случайности выборок являются случайными величинами. Все элементы выборки имеют то же распределение, что и генеральная совокупность: 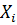 ∈ N (μ, σ), i = 1, 2, …, n. Среднее арифметическое также имеет нормальноераспределение:
∈ N (μ, σ), i = 1, 2, …, n. Среднее арифметическое также имеет нормальноераспределение:
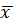 ∈ N (μ,
∈ N (μ,  ).
).
По формуле (2.16) получим
P(| 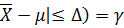 . (2.18)
. (2.18)
C другой стороны, заменяя в (1.45) X на 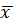 ,σ на σ/
,σ на σ/ 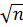 и ε на ∆ (допустимая точность оценки, допустимая погрешность), получим:
и ε на ∆ (допустимая точность оценки, допустимая погрешность), получим:
P(| 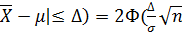 ) – 1 = 2Ф(
) – 1 = 2Ф( 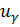 ) – 1 =γ, (2.19)
) – 1 =γ, (2.19)
где 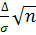 =
= 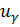 . Отсюда находим полуширину симметричного доверительного интервала
. Отсюда находим полуширину симметричного доверительного интервала
∆ = 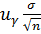 . (2.20)
. (2.20)
Используя соотношения (2.17) и (2.18), можно записать формулу для вычисления доверительного интервала:
P( 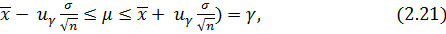
где выражение в скобках определяет полный доверительный интервал (2∆).
Вычислим значение переменной 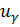 . На основании формулы (2.19) получим условие
. На основании формулы (2.19) получим условие
Ф( 
Согласно этому условию, из таблиц (см. приложение 3) найдем значение аргумента 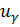 (его называют квантилемнормального распределения).
(его называют квантилемнормального распределения).
2.2.5 Доверительный интервал для среднего значения μ нормального распределения при неизвестном σ
Пусть задана генеральная совокупность с нормальным распределением X∈N(μ, σ), где значение стандартного отклонения σ неизвестно, то есть непосредственно воспользоваться нормальным распределением N(μ, σ) нельзя. Однако известно, что случайная величина
t = 
где S – несмещенная оценка стандартного отклонения (см. 2.14) генеральной совокупности, n – объем выборки, имеет распределение Стьюдента (t-распределение) с числом степеней свободы f = n – 1.
Для получения интервальной оценки – доверительного интервала потребуем, чтобы выполнялось условие
P(| 
где 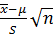 = t,а
= t,а 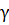 –доверительная вероятность.
–доверительная вероятность.
Величина  – квантиль (иначе - процентная точка) определяется по таблицам t-распределения Стьюдента (см. приложение 5). Соответственно для противоположного события t >
– квантиль (иначе - процентная точка) определяется по таблицам t-распределения Стьюдента (см. приложение 5). Соответственно для противоположного события t >  нужно использовать условие
нужно использовать условие
P (| 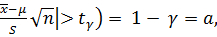
где 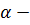 уровень значимости, обычно доверительная вероятность γ≫α, например, 0,95≫0,05.
уровень значимости, обычно доверительная вероятность γ≫α, например, 0,95≫0,05.
Число степеней свободы для t-распределения равно f = n – 1.
Преобразуя условие (2.24), имеем
P(g w:val="EN-US"/></w:rPr><m:t>-</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 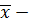
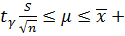
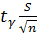 ) = γ, (2.25)
) = γ, (2.25)
где двухсторонний доверительный интервал указан в скобках. Полученная формула аналогична формуле (2.20). Здесь допустимая точность (вернее допустимая погрешность)
∆ = 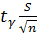 . (2.26)
. (2.26)
2.2.6 Доверительный интервал для дисперсии 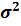 нормального распределения
нормального распределения
Предположим, что генеральная совокупность имеет нормальное распределение X ∈ N (μ, σ).Тогда случайная величина
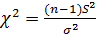 (2.27)
(2.27)
имеет 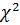 – распределение (распределение Пирсона) с числом степеней свободы f = n - 1. Случайная величина с
– распределение (распределение Пирсона) с числом степеней свободы f = n - 1. Случайная величина с 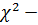 распределением принимает только неотрицательные значения. По таблицам
распределением принимает только неотрицательные значения. По таблицам 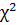 -распределения (см. приложение 4) можно найти квантиль χα2, удовлетворяющий следующему условию: P(χ2>χα2) = α = 1- γ, где α – уровень значимости (см. п.2.3 и рис. 23).
-распределения (см. приложение 4) можно найти квантиль χα2, удовлетворяющий следующему условию: P(χ2>χα2) = α = 1- γ, где α – уровень значимости (см. п.2.3 и рис. 23).
По таблицам 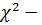 распределения всегда можно найти такие два числа
распределения всегда можно найти такие два числа 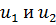 , которые удовлетворяли бы условию
, которые удовлетворяли бы условию
P( 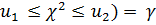 . (2.28)
. (2.28)
Таких пар чисел (границ) 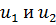 существует бесконечное множество. Чтобызафиксировать одну такую пару
существует бесконечное множество. Чтобызафиксировать одну такую пару  , введем дополнительное условие (симметричность по вероятности) (рисунок 24):
, введем дополнительное условие (симметричность по вероятности) (рисунок 24):
P( 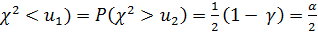 . (2.29)
. (2.29)
 Рисунок 23. Использование таблицы Рисунок 24. Нахождение чисел
Рисунок 23. Использование таблицы Рисунок 24. Нахождение чисел 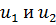
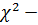 распределения
распределения
Из таблиц (приложение 4), используя условие (2.29), получаем 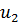 . Для нахождения
. Для нахождения 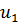 используем вероятность противоположного события
используем вероятность противоположного события
P( 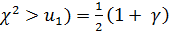 .(2.30)
.(2.30)
Заменяя в формуле (2.28) 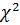 его значением из формулы (2.27) и выполняя преобразования, получаем
его значением из формулы (2.27) и выполняя преобразования, получаем
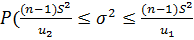 ) = γ, (2.31)
) = γ, (2.31)
где в скобках задан доверительный интервал для дисперсии 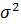 .
.
Извлекая квадратный корень из обеих сторон неравенства, определяющего доверительный интервал для дисперсии 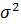 , получаем доверительный интервал для среднего квадратичного (стандартного) отклонения σ:
, получаем доверительный интервал для среднего квадратичного (стандартного) отклонения σ:
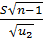 ≤ σ ≤
≤ σ ≤ 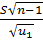 . (2.32)
. (2.32)
Задача 2.4
Найти доверительные интервалы для среднего значения µ, дисперсии σ2 и стандартного отклонения σ генеральных совокупностей при доверительной вероятности γ = 0,95, если из генеральной совокупности сделана выборка C (таблица 3 из задачи 2.3).
С доверительной вероятностью γ = 0, 95 по формуле (2.25) найдём доверительные интервалы для среднего значения (2.25), дисперсии σ2 по формуле (2.31) и стандартного отклонения σ по формуле (2.32), используя выборку C (n=6) .
Из таблицы распределения Стьюдента (приложение 5) найдём квантиль  = 2,571 (при f = 6-1 = 5;
= 2,571 (при f = 6-1 = 5; 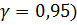 , а из таблицы
, а из таблицы
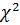 – распределения (приложение 4):
– распределения (приложение 4):
u1 = 0, 831 и u2 = 12,83, p = 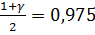 .
.
Найдем доверительные интервалы, при 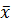 = -29,2; S2 = 46,968; S = 6,85; n =6 (см. задачу 2.3):
= -29,2; S2 = 46,968; S = 6,85; n =6 (см. задачу 2.3):
-по формуле (2.26) получаем ∆ = 2,571 * 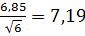 , затем интервалы:
, затем интервалы:
-для математического ожидания µ: ( -29,2 - 7,19) ≤ µ ≤ (-29,2 + 7,19), то есть -36,39 ≤ µ ≤ -22,01;
-для дисперсии: при  =
= 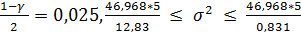 ,
,
а доверительный интервал для с.к.о σ :
18,30 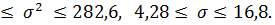
2.2.7 Определение необходимого объема выборки n
До сих пор мы рассматривали обработку готовых выборок с фиксированным объемом n. Часто стоит вопрос: какой объем должна иметь выборка, чтобы можно было получить результаты нужной точности? По закону больших чисел предпочтение отдается выборкам с большим объемом. Но обычно большой объем выборки требует и больших затрат для ее получения (и обработки). Поэтому на практике целесообразно использовать тот минимально необходимый объем, который позволяет получить удовлетворительные результаты по точности оценок при заданном уровне доверия γ.
Для вычисления доверительных интервалов среднего значения нормального распределения, можно, используя формулу (2.20), оценить необходимый объем выборки
n = 
Таким образом, объем выборки n прямо пропорционален (известной) дисперсии 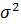 и квадрату квантиля нормального распределения
и квадрату квантиля нормального распределения 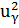 (он зависит от γ) и обратно пропорционален квадрату допустимой погрешности
(он зависит от γ) и обратно пропорционален квадрату допустимой погрешности 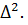
Если мы хотим получить интервал с большей доверительной вероятностью γ (вместе с этим увеличивается и 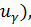 то следуетувеличить объем выборки n. Если мы хотим сузить доверительный интервал, то есть интервал неопределенности оценки, то должны увеличить объем выборки n. Итак, с помощью формулы (2.33) вычисляется необходимый объем выборки при известном σ.
то следуетувеличить объем выборки n. Если мы хотим сузить доверительный интервал, то есть интервал неопределенности оценки, то должны увеличить объем выборки n. Итак, с помощью формулы (2.33) вычисляется необходимый объем выборки при известном σ.
Однако, обычно значение σ неизвестно и тогда оценку для необходимого объема n выборки получаем из формулы (2.26):
n = 
По формуле (2.33), задавая σ, можно оценить соответствующий объем выборки n до получения самой выборки. По формуле (2.34) можно определить нужный объем выборки n после обработки результатов уже имеющейся пробной, небольшой серии опытов, по которой вычисляется несмещенная оценка дисперсии генеральной совокупности  .
.
Целесообразно, используя последовательно формулы (2.33) и (2.34) при заданном γ, находить уточненное значение объема выборки n, необходимого для получения требуемой точности (погрешности) оценки ∆.
Задача 2.5
Считая выборку C, заданную в задаче 2.3, пробной, определить минимальный объём выборки (количество необходимых опытов) n для нахождения доверительного интервала среднего значения µ при допустимой точности ∆ = 3 и доверительной вероятности γ = 0,99.
Для оценки минимального объёма планируемой основной выборки воспользуемся формулой (2.34) и пробной выборкой С.
При 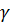 = 0,99, ∆ = 3 и n = 6 имеем: f = n-1 = 6 – 1 = 5; S = 6, 85;
= 0,99, ∆ = 3 и n = 6 имеем: f = n-1 = 6 – 1 = 5; S = 6, 85;
t0,99 = 4,03 (двусторонняя критическая область).
Предварительно минимально необходимый объём выборки равен
n = 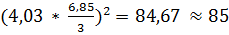 (опытов, измерений), тогда
(опытов, измерений), тогда
f = n-1 = 85-1= 84, а t0,99 = 2,64.
Уточнение значения необходимого объёма выборки:
n′ = (2,64∙6.85/3)² = 36,33 ≈ 37, при этом n′ t0,99 = 2,72 и
n″=(2,72∙6.85/3)² = 38,57 ≈ 39 опытов.
Дата добавления: 2018-11-26; просмотров: 903;











