Генеральная и выборочная дисперсии.
Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят такую характеристику, как генеральная дисперсия.
Определение. Генеральной дисперсией 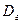 называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней
называется среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней 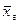 .
.
Если все значения  признака генеральной совокупности объёма N различны, то
признака генеральной совокупности объёма N различны, то
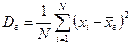 . (7)
. (7)
Если же значения признака 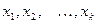 имеют соответственно частоты
имеют соответственно частоты 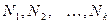 , причём
, причём 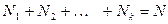 , то
, то
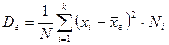 . (8)
. (8)
Пример. Генеральная совокупность задана таблицей распределения:
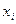
| ||||
|
Найти генеральную дисперсию.
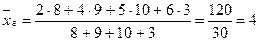 ,
,
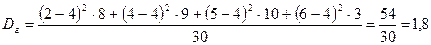 .
.
Определение. Генеральным средним квадратическим отклонением (стандартом) называется 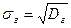 .
.
Дисперсия признака X, рассматриваемого, как случайная величина, равна 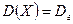 .
.
Тогда 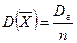 ,
, 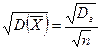
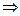
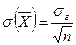 .
.
Величина 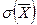 называется средней квадратической ошибкой.
называется средней квадратической ошибкой.
Определение. Выборочной дисперсией 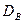 называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений признака X от выборочной средней 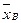 .
.
Если все значения 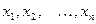 признака выборки объёма n различны, то
признака выборки объёма n различны, то
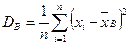 . (9)
. (9)
Если же значения 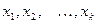 признака имеют соответственно частоты
признака имеют соответственно частоты 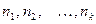 , причём
, причём 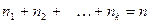 , то
, то
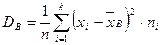 . (10)
. (10)
Пример. Выборочная совокупность задана таблицей распределения:
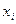
| ||||
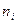
|
Найти выборочную дисперсию.
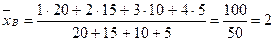 ;
;
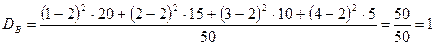 .
.
Выборочным средним квадратическим отклонением (стандартом) называется квадратный корень из выборочной дисперсии: 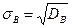 .
.
Пример. 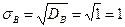
Будем считать значения 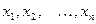 признака различными.
признака различными.
Выборочную дисперсию, рассматриваемую как случайную величину, будем обозначать 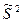 :
:
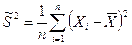 .
.
Теорема. Математическое ожидание выборочной дисперсии равно 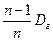 , т.е.
, т.е. 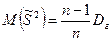 .
.
Дата добавления: 2021-01-26; просмотров: 512;











