Дифракция Фраунгофера

Дифракция от одной прямоугольной щели

Для наблюдения дифракции Фраунгофера источник света помещают настолько далеко от щели, что лучи можно считать практически параллельными. На практике источник света располагают в фокусе собирающей линзы, тогда лучи, вышедшие из линзы, будут параллельны (рис. 1).

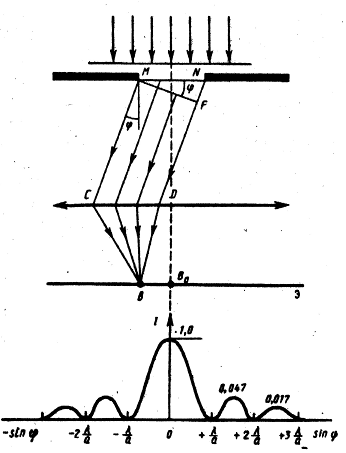Рис.1.

Пусть на щель шириной 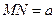падает монохроматический свет с длиной волны 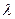. Из-за дифракции свет после щели распространяется во всех направлениях. Лучи, которые идут не отклоняясь, собираются линзой в точке D (экран находится в фокальной плоскости линзы). Точка D - главный фокус линзы. Рассмотрим лучи, которые дифрагируют под углом 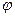. Они соберутся на экране в некоторой точке B (побочном фокусе линзы). Лучи, дифрагирующие под другими углами, соберутся в других точках на экране. В итоге экран будет освещен во многих местах, на нем будет чередование света и тени. Окажется в точке B минимум или максимум зависит от разности хода поступающих сюда волн. Щель является волновой поверхностью. По принципу Гюйгенса каждая точка ее есть источник вторичных волн. Найдем разность хода волн, приходящих в точку B. Для этого проведем фронт волны 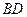. Точный расчет показывает, что оптические пути MB и FB одинаковы (геометрически путь FB короче, но здесь толще линза). Поэтому разность хода лучей 1 и 2 равна 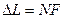. Проведем систему плоскостей параллельных MF на расстоянии 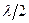друг от друга. Разность хода разделиться на участки длиной 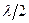, а щель на полоски, называемые зонами Френеля.

Площади этих зон одинаковы, поэтому по принципу Гюйгенса-Френеля они испускают волны равной интенсивности. Разность хода между соответствующими точками соседних полосок по построению равна 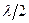. Поэтому, если в щели укладывается четное число зон Френеля, они попарно друг друга погасят. Тогда в точке B будет наблюдаться минимум, если нечетное, то одна зона окажется непогашенной и в точке B будет максимум.

Число зон Френеля равно 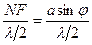. Если это число четное, то мы получаем условие минимума:

,

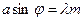если нечетное, то условие максимума:

.

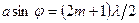Величина называется порядком дифракционного спектра.

В направлении 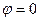наблюдается самый интенсивный центральный максимум нулевого порядка, в этом случае щель действует как одна зона Френеля и интенсивность света велика.

Если на щель падает белый свет, то для каждой длины волны будет соответствовать свой угол 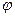и полоски будут окрашены. Ближе к центру будет фиолетовый свет, конец полоски будет красный. Центральный максимум будет общим для всех длин волн, так что центр дифракционной картина будет представляться в виде белой полоски.

Дифракционная картина зависит от соотношения 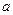и :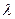

1. Если 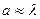, то наблюдается описанная дифракционная картина.

2. Если 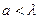, то в щели укладывается только одна зона Френеля при всех значениях 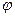, и на экране будет наблюдаться расплывшийся нулевой максимум.

3. 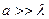, 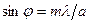. Углы будут мало отличаться для малых 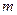. На экране будет видно равномерно освещенное изображение щели и только у краев его размытие (при больших значениях ).

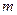От одной щели трудно наблюдать дифракционную картину из-за малой интенсивности. Поэтому обычно используется дифракционная решетка.

Дифракционная решетка

Дифракционная решетка – это система одинаковых параллельных щелей, разделенных равными промежутками (рис. 2).

Рис.2.

Величина 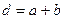называется постоянной дифракционной решетки.

На стеклянную пластинку алмазом наносят царапины. Там где царапина – непрозрачный промежуток решетки. На один миллиметр решетки наносят от 50 до 500 штрихов. Рассмотрим дифракцию от двух щелей (р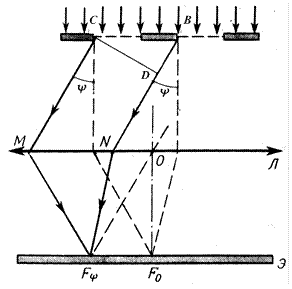ис. 3).

Рис.3

Если под каким-то углом 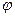каждая щель не пропускает свет, то и вся решетка не пропускает (в каждой щели укладывается четное число зон Френеля). Условие главных минимумов для решетки совпадает с условием минимумов для одной щели:

.

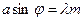Если каждая из щелей дает максимум, то на экране может быть максимум или минимум в зависимости от разности хода лучей 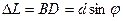. Щели когерентные источники, поэтому лучи интерферируют и дают максимумы или минимумы. Если в величине 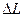укладывается четное число полуволн, то наблюдается максимум:

,

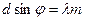если нечетное, то минимум:

.

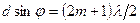Итак, полная дифракционная картина для двух щелей определяется из условий:

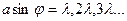- главные минимумы.

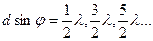- дополнительные минимумы.

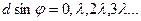- главные максимумы.

Таким образом, между двумя главными максимумами располагается один дополнительный минимум. Можно показать, что между двумя главными максимумами в случае трех щелей будет располагаться два дополнительных минимума, при четырех щелях – три.

В случае 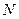щелей условием дополнительных минимумов будет выражение:

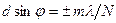, где .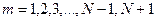

Число 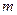принимает все целочисленные значения, кроме 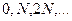при которых условие дополнительных минимумом переходит в условие главных максимумов.

Следователь но в случае N щелей между двумя главными максимумами располагаются N-1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон. Вторичные или дополнительные максимумами обусловлены интерференцией света от более далеких щелей.

Чем больше щелей, тем больше световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, которые становятся более интенсивными и острыми. На рис. 4. качественно представлена дифракционная картина от восьми щелей.

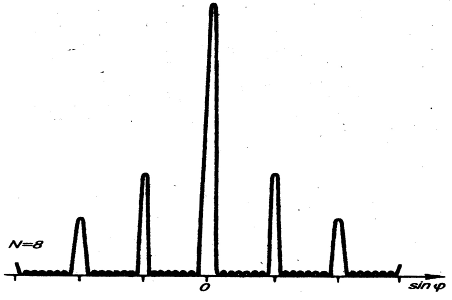Рис.4.

Число главных максимумов зависит от отношения периода решетки к длине волны.

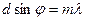отсюда 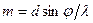, так как 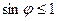, то .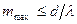

Полное число максимумов равно: .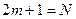

Дифракционная решетка используется как спектральный прибор. При пропускании через решетку белого света, все максимумы, кроме главного, разлагаются в спектр (как было уже показано в случае дифракции на одной щели).

Голография

Голография в переводе с греческого – полная запись (Голос – весь, грифо – пишу). Голография – это особый способ записи на фотопластинке структуры световой волны, отраженной предметом. При освещении голограммы пучком света эта волна почти полностью восстанавливается и создается впечатление, что наблюдается сам предмет.

Обычный фотографический способ получения изображения предмета основан на регистрации с помощью фотопластинки различий в интенсивности света, рассеваемого разными малыми элементами поверхности предмета. Но при этом не учитывается расстояние, откуда идет свет. В результате получается плоское изображение предмета.

Английский физик Габор (1948) высказал идею принципиально нового метода получения объемных изображений объектов. Он предложил регистрировать при помощи фотопластинки не только интенсивности но и фазы рассеянных предметом волн, воспользовавшись для этого явлением интерференции волн. Распределение интенсивности в интерференционной картине определяется как амплитудой интерферирующих волн, так и разностью их фаз: 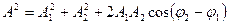. Свой метод Габор назвал голографией. Суть метода поясняется на р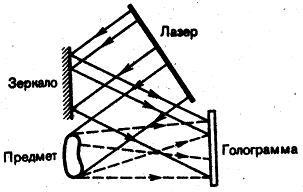ис. 5.

Рис.5

Лазерный пучок делится на две части, одна его часть отражается зеркалом на фотопластинку (опорная волна), а вторая попадает на фотопластинку, отразившись от предмета (предметная волна). Опорная и предметная волны когерентны и они интерферируют на фотопластинке. Интерференционная картина, зафиксированная на фотопластинке после ее проявления, называется голограммой предмета. Голограмма в отличие от фотографического негатива объекта, не имеет внешнего сходства с предметом. Она представляет замысловатый узор из чередующихся малых областей различного почернения эмульсии. Восстановление изображение по его голограмме проясняется на рис.8.

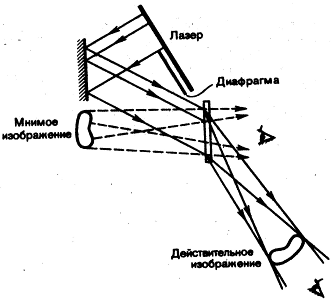Рис.6

Для восстановления изображения голограмма помещается в тоже положение, где она находилась на стадии получения. Ее освещают опорным пучком того же лазера. Вторая часть лазера перекрывается диафрагмой. В результате дифракции света на интерференционной структуре голограммы образуется два объемных изображения предмета. Одно мнимое, которое находится на том же месте, где был предмет, и действительное висячее.

Мнимое изображение видно при наблюдении сквозь голограмму как через окно. Интерференционная картина в каждой точке голограммы определяется светом, рассеянным всеми точками предмета. Поэтому каждый участок содержит сведения обо всем предмете. С помощью малого осколка голограммы можно восстановить весь предмет. Однако уменьшение размеров голограммы приводит к ухудшению четкости получаемого изображения (чем меньше света, тем меньше света на ней дифрагирует на стадии восстановления изображения).

Применяется голография для записи и хранения информации. На одну и ту же пластинку можно последовательно записать несколько различных голограмм, меняя угол падения опорной волны. На одной фотопластинке можно записать книгу объемом более тысячи страниц. Голография также применяется для кодирования информации. Чтобы восстановить по голограмме изображение предмета нужно точно знать положение фотопластинки при получении голограммы.