Дифракция на диске.

Пусть свет из точки источника 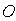(рис. 8.15) освещает непрозрачный диск радиуса 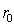, за которым на прямой, перпендикулярной плоскости диска и проведенной через его центр, располагается точка наблюдения 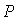. Как и выше, будем считать, что размер диска во много раз меньше расстояний от диска до источника 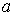и от диска до точки наблюдения .

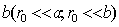Предположим, что диск из точки наблюдения 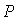'закрывает' 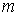зон Френеля. Тогда амплитуда света 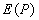в точке наблюдения будет равна алгебраической сумме амплитуд волн 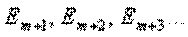открытых зон Френеля:

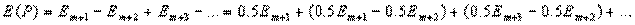Учитывая, что амплитуды соседних зон Френеля примерно равны друг другу, однотипные выражение в скобках можно положить равными нулю, и тогда получим

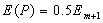(8.15)

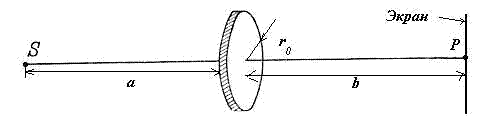Рис.8.15

Отсюда следует, что в центре дифракционной картины, создаваемой диском, всегда наблюдается светлое пятно, независимо от размеров диска. В истории физики это свойств зон Френеля явилось доказательством волновой природы света. С точки зрения современников Френеля наблюдение светлого пятна в центре геометрической тени препятствия, освещаемого светом, казалось абсурдным, что и послужило основанием для Пуассона (1781-1853) возразить против волновой природы света. Для проверки этого возражения Араго (1786-1853) поставил опыт, которым действительно наблюдалось светлое пятно в центре геометрической тени диска (рис. 8.16), освещаемого светом, получившее название пятно Араго- Пуассона. Справедливости ради, необходимо отметить, что наблюдение пятна было отмечено задолго до опыта Араго - ещё в 1713г. Делилем, а 1723г. Моральди. Однако, поскольку природа этого явления была непонятна, то наблюдения оказались незамеченными.

Дифракционная картина от диска, наблюдаемая на экране (рис8.16), имеет характер чередующихся тёмных и светлых колец, в центре которых находится светлое пятно.

Пусть для определённости диск закрывает только одну зону Френеля. Тогда в центре дифракционной картины диска амплитуда волны определяется разностью амплитуд волны источника, когда нет никакого экрана, и волны от отверстия, имеющего размер первой зоны Френеля. Учитывая, что амплитуда волны от первой зоны Френеля в два раза больше, чем амплитуда волны источника в точке наблюдения, получаем, что интенсивность волны за диском равна интенсивности волны источника в отсутствии диска.

Если же диск закрывает две зоны Френеля, то в центре дифракционной картины диска амплитуда волны определяется амплитудой волны источника, когда нет никакого экрана, поскольку амплитуду волны, создаваемой отверстием того же диаметра, что и диск, приближённо можно полагать равной нулю. Проведенные

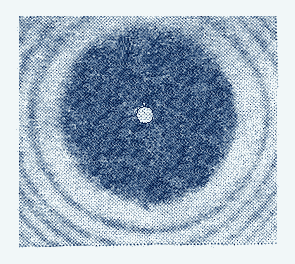Рис.8.16

рассуждения, очевидно, справедливы для диска, открывающего произвольное число (не очень большое) чётных или нечётных зон Френеля.

Таким образом, амплитуда волны в центре дифракционной картины от диска любого размера равна половине амплитуды волны от первой открытой зоны Френеля, что совпадает с результатом проведенных выше расчётов. На периферии дифракционной картины от диска распределение интенсивности в основном определяется амплитудой волны источника, на которую 'накладываются' затухающие по мере удаления от центра картины колебания волн от частично открытых зон Френеля отверстием в непрозрачном экране того же диаметра, что и рассматриваемый диск.

Рассмотрим вид дифракционной картины в зависимости от размера диска. Если размер диска во много раз меньше первой зоны Френеля, то наблюдается практически равномерное освещение экрана - диск как бы не отбрасывает тени. Если размер диска закрывает 'много' зон Френеля, в центре дифракционной картины светлого пятна практически не видно т.к. 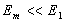, освещённость картины в области геометрической тени практически равна нулю, а дифракционные кольца наблюдаются в узкой области на границе свет тень.

Заключение

При построении векторных диаграмм необходимо помнить о векторном характере амплитуды. Сложение амплитуд лучше производить методом треугольника. Зоны Френеля делятся на подзоны таким образом, чтобы фаза вторичных волн в подзоне оставалась постоянной. В дифракции Френеля амплитуда является убывающей величиной и это необходимо учитывать при построении векторной диаграммы. Распределение интенсивности при дифракции на круглом отверстии зависит от того четное или нечетное число зон Френеля укладывается в это отверстие. При нечетном числе зон Френеля в центре дифракционной картины всегда наблюдается максимум, а при четном –минимум.

В дифракции Фраунгофера используются плоские волны, следовательно, амплитуда не зависит от расстояния, пройденного волной. Поэтому распределение интенсивности отличается от распределения в дифракции Френеля.