Дифракция в опыте Юнга.

Анализируя опыт Юнга, мы вывели, что распределение интенсивности в интерференционной картине определяется следующим выражением

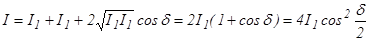(10.1)

Напомним, что d - разность фаз складываемых колебаний.

Из (10.1) следует, что максимумы интерференционной картины имеют одну и ту же высоту, т.е. распределение интенсивности выглядит следующим образом,

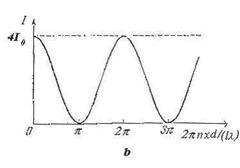
Рис.10.1

Выводя уравнение (10,1), мы предполагали, что щели в опыте Юнга являются бесконечно узкими, т.е. по сути точечными источниками, в этом случае центральный дифракционный максимум от каждой щели размывается на весь экран ( см. 9.17). Разумеется, этого никогда не бывает с реальными щелями. Дифракция изменяет амплитуду вторичных волн, идущих от щели, в результате интенсивность максимумов разных порядков уже не может быть одинаковой.

Вычислим теперь распределение интенсивности для интерференционной картины в опыте Юнга с учетом дифракции. Предположим, что обе щели имеют одинаковую ширину aи центры их находятся на расстоянии d друг от друга, так как расстояние от щелей до экрана велико по сравнению с расстоянием d, то дифракционные картины от каждой щели в отдельности практически совпадают . Е₀- амплитуда светового вектора волны, падающей на диафрагму с двумя щелями. На экран приходит световая волна, распространяющаяся под углом дифракции q, от каждой щели с результирующей амплитудой

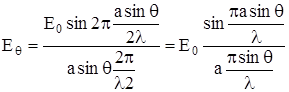(10.2)

Эти волны когерентны, поэтому они будут интерферировать, и на экране будет наблюдаться интерференционная картина. Чтобы описать распределение интенсивности на экране необходимо найти амплитуду светового вектора. Так как, интенсивность пропорциональна квадрату амплитуды, то амплитуда в максимумах интерференционной картины будет определяться формулой:

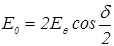(10.3)

Подставим (10.2) в (10.3) получаем окончательное выражение для амплитудного значения светового вектора в любой точке экрана:

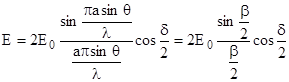(10.4)

Следовательно, распределение интенсивности на экране определяется выражением

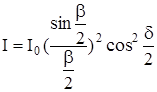(10.5)

Исследуем влияние дифракции на интерференционную картину согласно выражению (10.5). Мы помним, что разность фаз крайних лучей, идущих под углом дифракции q, при дифракции на одной щели (10.4) определяется

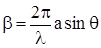(10.6)

Разность фаз при интерференции от щелей, расположенных на расстоянии d, исходя из связи разности хода с разностью фаз, определяется выражением

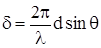(10.7)

Дифракционные минимумы будут определяться условием ,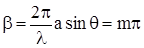

Или

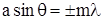
И их расположение определиться условием:

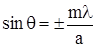(10.8)

На рисунке, sinq=sinj

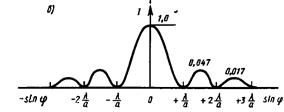
рис.10.2

Найдем расположение интерференционных минимумов, используя выражение (10.7),

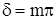
или через разность хода

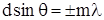
и расположение интерференционных минимумов

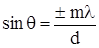(10.9)

Сравним условия (108) и (10.9). Если 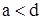, то дифракционные ммаксимумы более широкие по сравнению с интерференционными максимумами, поэтому интерференционные максимумы вписываются внутрь дифракционных максимумов. На рис.10.3 d==3a

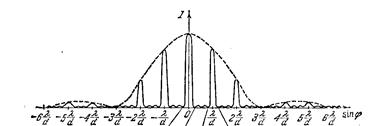
рис10.3

Число интерференционных полос, умещающихся в центральном дифракционном максимуме, зависит только от соотношения d/a и не зависит от длины волны.

Отдельно следует обсудить значение интенсивности центрального дифракционного максимума. Если бы колебания от щелей, образующие центральный максимум были некогерентными, результирующая картина от 2 щелей отличалась бы от картины, создаваемой одной щелью,

лишь тем, что все интенсивности возросли бы в 2 раза. Однако колебания от различных щелей являются когерентными; поэтому результирующая интенсивность будет определяться результирующей амплитудой. Так как центральный максимум образуется волнами, не имеющими разности хода, то световые векторы алгебраически складываются, т.е. Е=2Е_q, а интенсивность увеличится в 4 раза.