Элементы геометрической оптики.
Основные законы геометрической оптики.
Еще до установления природы света были известны следующие основные законы оптики:
Закон прямолинейного распространения света.
Длины световых волн воспринимаемых глазом очень малы (порядка 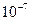 м). Поэтому рассмотрение видимого света приближенно можно рассматривать отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В этом приближении законы оптики можно сформулировать на языке геометрии. Поэтому раздел оптики, в котором пренебрегают конечностью длин волн (
м). Поэтому рассмотрение видимого света приближенно можно рассматривать отвлекаясь от его волновой природы и полагая, что свет распространяется вдоль некоторых линий, называемых лучами. В этом приближении законы оптики можно сформулировать на языке геометрии. Поэтому раздел оптики, в котором пренебрегают конечностью длин волн ( 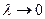 ) называется геометрической оптикой. Другое название этого раздела лучевая оптика. Свет в оптически однородной среде распространяется прямолинейно. Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их точечными источниками света (источники, размеры которых значительно меньше освещаемого предмета и расстояния от него). Этот закон нарушается при прохождении света через малые отверстия или освещении малых преград.
) называется геометрической оптикой. Другое название этого раздела лучевая оптика. Свет в оптически однородной среде распространяется прямолинейно. Доказательством этого закона является наличие тени с резкими границами от непрозрачных предметов при освещении их точечными источниками света (источники, размеры которых значительно меньше освещаемого предмета и расстояния от него). Этот закон нарушается при прохождении света через малые отверстия или освещении малых преград.
Закон независимости световых лучей.
Эффект производимый отдельным лучом, не зависит от того действуют ли одновременно остальные лучи или они устранены. Лучи при пересечении не изменяют друг друга. Пересечение лучей не мешает каждому из них распространяться независимо друг от друга. Этот закон справедлив лишь при небольших интенсивностях света. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей нарушается.
Если свет падает на границу двух оптически прозрачных сред, то падающий луч разделяется на два: отраженный и преломленный, направления которых задаются законами отражения и преломления.
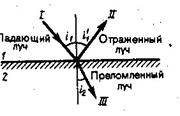
Закон отражения света: отраженный луч лежит в одной плоскости с падающим и перпендикуляром, проведенным к границе раздела сред в точке падения. При этом угол падения равен углу отражения (рис.1)
|
| Рис. 1. |
Закон преломления света: преломленный луч лежит в одной плоскости с падающим и перпендикуляром, проведенным к границе раздела сред в точке падения. При этом отношение синуса угла падения к углу отражения есть величина постоянная для данных сред: 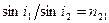 , где
, где 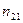 - относительный показатель преломления второй среды относительно первой.
- относительный показатель преломления второй среды относительно первой.
Если луч шел из второй среды в первую, то вследствие обратимости световых лучей относительный показатель преломления первой среды относительно второй 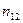 записывается в виде:
записывается в виде: 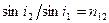 . Следовательно,
. Следовательно, 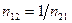 .
.
Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления: 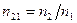 .
.
Абсолютным показателем преломления называется величина равная отношению скорости света в вакууме 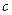 к фазовой скорости волны в среде
к фазовой скорости волны в среде 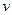 :
: 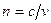 . Фазовая скорость волны в среде определяется величинами магнитной
. Фазовая скорость волны в среде определяется величинами магнитной 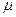 и электрической
и электрической 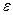 проницаемости среды и связана со скоростью света по формуле:
проницаемости среды и связана со скоростью света по формуле: 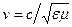 . Следовательно, абсолютный показатель преломления среды равен:
. Следовательно, абсолютный показатель преломления среды равен: 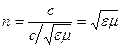 .
.
Учитывая определение абсолютного показателя преломления, закон преломления можно записать в следующем виде:
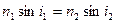 .
.
Значения абсолютных показателей преломления приводятся в физических таблицах.
Если свет распространяется в среду с большим показателем преломления в среду с меньшим показателем преломления 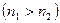 , то угол отражения больше угла падения:
, то угол отражения больше угла падения: 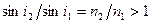 . С увеличением угла падения увеличивается и преломленный угол до тех пор, пока при некотором угле падения
. С увеличением угла падения увеличивается и преломленный угол до тех пор, пока при некотором угле падения 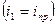 угол преломления не окажется равным
угол преломления не окажется равным 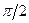 . Угол
. Угол 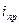 называется предельным углом. Преломленный луч при этом скользит вдоль раздела сред. При углах падения
называется предельным углом. Преломленный луч при этом скользит вдоль раздела сред. При углах падения 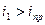 весь падающий свет полностью отражается в первую среду. Это явление называется полным отражением. Подставив в закон преломления
весь падающий свет полностью отражается в первую среду. Это явление называется полным отражением. Подставив в закон преломления 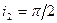 , получим
, получим 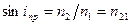 . Отсюда
. Отсюда
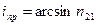 .
.
При полном внутреннем отражении потерь интенсивности света не происходит.
Явление полного отражения используется в призмах полного отражения. Показатель преломления стекла равен 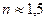 , поэтому предельный угол отражения на границе стекло-воздух равен
, поэтому предельный угол отражения на границе стекло-воздух равен 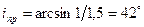 . Свойство полного отражения используется в различных оптических приборах для поворота лучей и пр. (рис. 2).
. Свойство полного отражения используется в различных оптических приборах для поворота лучей и пр. (рис. 2).
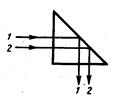 Поворот луча на
Поворот луча на 
|  Поворот изображения
Поворот изображения
|
 Оборачивание лучей
Оборачивание лучей
|
| Рис. 2. |
Тонкие линзы. Изображение предметов с помощью собирающей линзы.
Виды линз. Главная оптическая ось линзы.
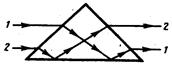
Линзой называется прозрачное для света стекло, ограниченное двумя сферическими поверхностями (одна из поверхностей может быть плоской). Линзы, у которой середина толще, чем края, называются выпуклыми, а те, у которых края толще середины – вогнутыми. Выпуклая линза является собирающей, а вогнутая – рассеивающей. Различные виды линз показаны на рис.3: 1 – двояковыпуклая, 2 – двояковогнутая, 3 – плосковыпуклая, 4 – плосковогнутая, 5 – выпукловогнутая, 6 – вогнутовыпуклая.
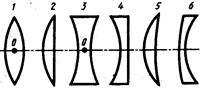 Рис. 3.
Рис. 3.
|
Прямую 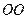 , проходящую через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы.
, проходящую через центры сферических поверхностей, ограничивающих линзу, называют главной оптической осью линзы.
Оптический центр линзы. Побочные оптические оси.
Линзу, у которой толщина пренебрежимо мала по сравнению с радиусами кривизны поверхностей линзы и расстоянием от предмета до линзы называют тонкой. В тонкой линзе вершины шаровых сегментов расположены на столько близко, что их можно принять за одну точку. Эту лежащую на главной оптической оси точку 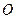 , через которую световые лучи проходят не изменяя своего направления, называют оптическим центром тонкой линзы. Любую прямую, проходящую через оптический центр линзы называют оптической осью. Все оптические оси, кроме главной, называют побочными оптическими осями.
, через которую световые лучи проходят не изменяя своего направления, называют оптическим центром тонкой линзы. Любую прямую, проходящую через оптический центр линзы называют оптической осью. Все оптические оси, кроме главной, называют побочными оптическими осями.
Главные фокусы и фокусные расстояния линзы.
Точку 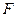 на главной оптической оси, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси, называют главным фокусом линзы (рис. 4, рис. 5). Любая линза имеет два главных фокуса, расположенные по обе ее стороны симметрично оптическому центру.
на главной оптической оси, в которой пересекаются после преломления лучи, падающие на линзу параллельно главной оптической оси, называют главным фокусом линзы (рис. 4, рис. 5). Любая линза имеет два главных фокуса, расположенные по обе ее стороны симметрично оптическому центру.
У собирающей линзы (рис. 4) фокусы действительны, а у рассеивающей (рис. 5) –мнимые. Расстояние 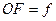 от оптического центра линзы до ее главного фокуса называют фокусным. У собирающей линзы фокусное расстояние считают положительным, а у рассеивающей – отрицательным.
от оптического центра линзы до ее главного фокуса называют фокусным. У собирающей линзы фокусное расстояние считают положительным, а у рассеивающей – отрицательным.
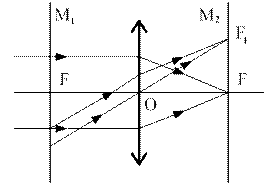 Рис.4 Собирающая линза
Рис.4 Собирающая линза
| 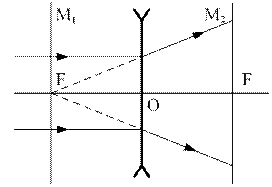 Рис.5 Рассеивающая линза
Рис.5 Рассеивающая линза
|
Фокальные плоскости линзы и их свойства.
Плоскости, проходящие через главный фокус тонкой линзы перпендикулярно главной оптической оси, называются фокальными. У каждой линзы две фокальные плоскости ( 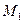 и
и 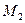 на рис. 4 и 5), расположенные по обе стороны от линзы.
на рис. 4 и 5), расположенные по обе стороны от линзы.
Лучи света, падающие на собирающую линзу параллельно какой-либо ее побочной оптической оси, после преломления в линзе сходятся в точке пересечения этой оси с фокальной плоскостью (в точке 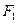 на рис.4). Эту точку называют побочным фокусом.
на рис.4). Эту точку называют побочным фокусом.
Фокусное расстояние и оптическая сила линзы.
Величина 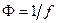 называется оптической силой линзы. Чем больше
называется оптической силой линзы. Чем больше 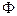 , тем меньше фокусное расстояние
, тем меньше фокусное расстояние 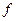 , и, следовательно, тем сильнее преломляются лучи.
, и, следовательно, тем сильнее преломляются лучи.
За единицу оптической силы принимают оптическую силу такой линзы, фокусное расстояние которой равно 1м. Эту единицу называют диоптрией ( 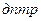 ).
).
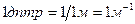 .
.
Собирающие линзы имеют положительную оптическую силу, рассеивающие – отрицательную.
Вывод формулы тонкой линзы на основе геометрического построения хода лучей.
Пусть перед собирающей линзой находится светящийся предмет 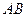 (рис. 6). Для построения изображения этого предмета необходимо построить изображения его крайних точек, причем выбирать такие лучи, изображение которых окажется наиболее простым. Таких лучей, в общем случае, может быть три:
(рис. 6). Для построения изображения этого предмета необходимо построить изображения его крайних точек, причем выбирать такие лучи, изображение которых окажется наиболее простым. Таких лучей, в общем случае, может быть три:
1. луч 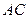 , параллельный главной оптической оси, после преломления проходит через главный фокус линзы, то есть идет по прямой
, параллельный главной оптической оси, после преломления проходит через главный фокус линзы, то есть идет по прямой 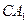 .
.
2. луч 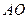 , идущий через оптический центр линзы, не преломляется и тоже приходит в точку
, идущий через оптический центр линзы, не преломляется и тоже приходит в точку 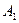 .
.
3. луч 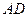 , идущий через передний фокус линзы, после преломления идет параллельно главной оптической оси по прямой
, идущий через передний фокус линзы, после преломления идет параллельно главной оптической оси по прямой 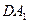 .
.
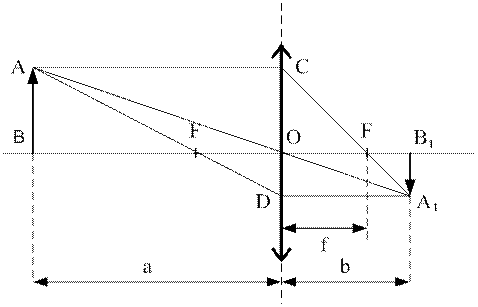 Рис.6.
Рис.6.
|
Все три указанных луча пересекаются в точке 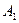 , где получается действительное изображение точки
, где получается действительное изображение точки 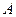 . Опустив перпендикуляр на главную оптическую ось, находим точку
. Опустив перпендикуляр на главную оптическую ось, находим точку 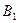 , являющуюся изображением точки
, являющуюся изображением точки 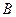 . Для построения изображения достаточно двух из перечисленных лучей.
. Для построения изображения достаточно двух из перечисленных лучей.
Используя рис. 6 выведем формулу тонкой линзы. Из подобия треугольников 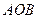 и
и 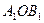 следует соотношение
следует соотношение 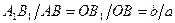 . Из подобия треугольников
. Из подобия треугольников 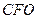 и
и 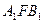 следует
следует 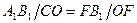 . Так как
. Так как 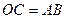 , то
, то 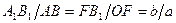 . Поскольку
. Поскольку 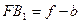 , а
, а 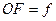 , то последнюю формулу можно переписать в следующем виде:
, то последнюю формулу можно переписать в следующем виде: 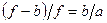 . Упрощая это выражение, получаем формулу:
. Упрощая это выражение, получаем формулу:
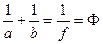 .
.
Это выражение называется формулой тонкой собирающей линзы. У рассеивающей линзы фокусное расстояние отрицательное 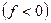 , поэтому формула тонкой рассеивающей линзы имеет вид:
, поэтому формула тонкой рассеивающей линзы имеет вид:
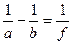 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Дифракция Фраунгофера | | | Теория атома водорода по Бору |
Дата добавления: 2016-05-28; просмотров: 3079;











