Нормальное уравнение прямой.

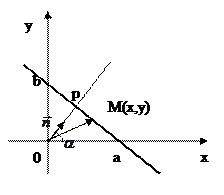Рассмотрим некоторую прямую L.

Проведём через начало координат прямую, перпендикулярную к L и обозначим через Р точку пересечения этих прямых. На прямой ОР возьмем единичный вектор .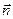

Поставим перед собой цель: выразить уравнение прямой L чез два параметра

1) длину p отрезка ОР;

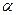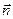2) угол между и осью Ох.

Так как 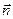- единичный вектор, то .

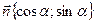точка М(х, у) 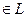, тогда и только тогда, когда 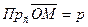, , 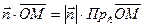т.к. 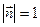, то .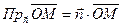

Имея ввиду, что 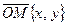, а 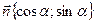, получим .

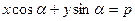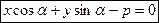- нормальное (нормированное) уравнение прямой, где
р – длина перпендикуляра, опущенного из начала координат на прямую;
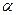- угол, который этот перпендикуляр образует с положительным направлением оси Ох.

Алгоритм приведения общего уравнения прямой к нормальному виду:

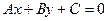
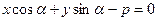
Т.к. данные уравнения определяют одну и ту же прямую, то существует такое число 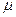, при котором 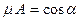; ; 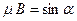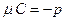. Первые два тождества возведём в квадрат и просуммируем: + , , - .

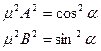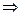
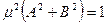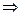
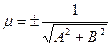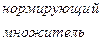Остаётся уточнить, какой из знаков 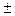следует взять в данной формуле. Так как расстояние 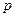всегда неотрицательно, то из третьего тождества заключаем, что знак нормирующего множителя противоположен знаку С.

Итак, для приведения общего уравнения прямой 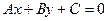к нормальному виду следует умножить его на нормирующий множитель, знак которого противоположен знаку свободного члена С.

Введём теперь фундаментальное понятие – отклонение произвольной точки М от данной прямой L.

Пусто число d – это расстояние от точки М до прямой L.

Назовём отклонением 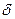точки М от прямой L число +d в случае, если т.М и начало координат т. О лежат по разные стороны от прямой L и число -d в случае, если т.М и начало координат т. О лежат по одну сторону от прямой L.

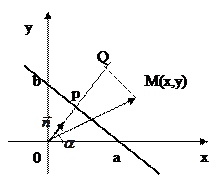Спроектируем точку М на направление вектора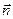

PQ = 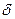= OQ – p,

,

.

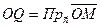
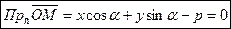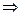
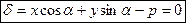Итак, для нахождения отклонения 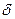точки 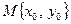от прямой L, следует в левую часть нормального уравнения прямой L подставить на место х и у координаты 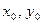точки М.