Основные свойства капельных жидкостей

Одной из основных механических характеристик жидкости явля­ется ее плотность.

Плотностью 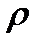(кг/м³) называют массу жидкости, заключенную в единице объема; для однородной жидкости

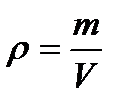(1.5)

где m – масса жидкости в объеме V.

Удельным весом 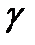(Н/м³) называют вес единицы объема жидкости, т. е,.

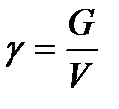(1.6)

где G — вес жидкости в объеме V.

Связь между удельным весом y и плотностью ρ легко найти, если учесть, что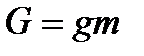

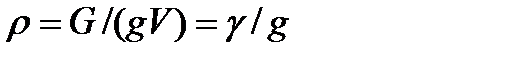(1.7)

Если жидкость неоднородна, то формулы (1.4) и (1.5) определяют лишь среднее значение удельного веса или плотности в Данном объеме. Для определения истинного значения у и р в данной точке следует рассматривать объем, уменьшающийся до нуля, и искать предел соответствующего отношения.

Применяют еще относительную плотность жидкости б, равную отношению плотности жидкости к плотности воды при 4 ^СС:

б = ρ_ж/ρ_вод (1.8)

Коротко рассмотрим основные физические свойства капельных жидкостей.

А) Сжимаемость, или свойство жидкости изменять свой объем под действием давления, характеризуется коэффициентом р_р (м²/Н) объемного сжатия, который представляет собой относительное изме­нение объема, приходящееся на единицу давления, т. е.

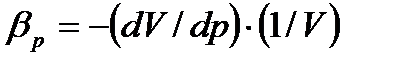(1.9)

Знак минус в формуле обусловлен тем, что положительному при­ращению давления р соответствует отрицательное приращение (т. е. уменьшение) объема V.

Рассматривая конечные приращения Δр = р - p₁ и ΔV = V–V₁ и считая β_p постоянным, получаем

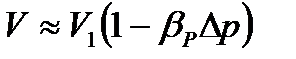(1.10)

или, учитывая равенство (1.8), находим приближенную формулу для определения плотности

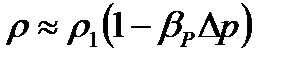(1.11)

где ρ₁ и ρ — плотности при давлениях p₁ и р, Величина, обратная коэффициенту β_р, представляет собой объем­ный модуль упругости K. Через модуль К и конечные разности формулу (1.8) можно пере­писать в виде зависимости

ΔV/V = - Δр/ К (1.12)

которую называют обобщенным законом Гука.

Выразив объем через плотность, получим

K = — dp/[ρd(1/ρ)] = ρ dρ /dρ или K/p = dp/dp = c², (1.13)

где с — скорость распространения продольных волн в упругой среде, равная скорости звука.

Для капельных жидкостей модуль К несколько уменьшается с увеличением температуры и, возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего лишь на 1/20 000 часть. Такого же порядка модуль упругости и для других капельных жидкостей, на­пример для минеральных масел он равен приблизительно 1200 МПа.

Как следует из формулы (1.9), при повышении давления воды, например, до 40 МПа ее плотность повышается лишь на 2 %, а масла — на 3 %. Поэтому в большинстве случаев капельные жид­кости можно считать практически несжимаемыми, т. е. принимать их плотность не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкостей следует учитывать.

Различают адиабатный и изотермический модуль упругости. Первый больше второго приблизительно в 1,5 раза и проявляется при быстротечных процессах сжатия жидкости без теплообмена. Приведенные выше значения К являются значениями изотермиче­ского модуля.

Б). Температурное расширение характеризуется коэффициентом рг объемного расширения, который представляет собой относительное изменение объема при изменении температуры Т на 1 °С и постоян­ном давлении, т. е.

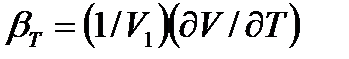(1.14)

Рассматривая конечные приращения ΔV = V — V_l и ∆Т =Т – Т₁ и принимая β_Т постоянным, получаем

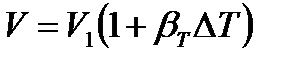(1.15)

а учитывая равенство (1.8), находим приближенную формулу

ρ = ρ₁/(1 + β_тΔТ) (1.16)

где ρ₁ и ρ — плотности при температурах Т₁и Т.

В). Сопротивление растяжению внутри капельных жидкостей по молекулярной' теории может быть весьма значительным. При опытах с тщательно очищенной и Дегазированной водой В ней были получены кратковременные напряжения растяжения до 23 — 28 МПа. Однако технически чистые жидкости, содержащие взвешенные твердые ча­стицы и мельчайшие пузырьки газов, не выдерживают даже незначи­тельных напряжений растяжения. Поэтому в дальнейшем будем считать, что напряжения растяжения в капельных жидкостях не­возможны.

Г). На поверхности раздела жидкости и газа действуют силы поверхностного натяжения, стремящиеся придать объему жидкости сферическую форму и вызывающие некоторое дополнительное дав­ление. Однако это давление заметно сказывается лишь при малых объемах жидкости и для сферических объемов (капель) определяется формулой

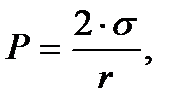
где σ — коэффициент поверхностного натяжения жидкости; r- радиус сферы.

Коэффициент σ имеет следующие значения (Н/м) для разных жидкостей, граничащих с воздухом при температуре 20 °С: для, воды 73^-3, спирта 22,5^-3, керосина 27^-3, ртути 460*10^-3. С ростом темпе­ратуры поверхностное натяжение уменьшается.

В трубках малого диаметра дополнительное давление, обуслов­ленное поверхностным натяжением, вызывает подъем (или опускание) жидкости относительно нормального уровня, характеризующий
капиллярность жидкости.

Высоту подъема смачивающей жидкости (или опускание, несмачивающей жидкости) в стеклянной трубке диаметром d определяют по формуле для полусферического мениска

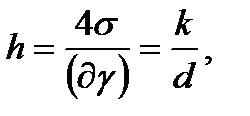(1.17)

где k (мм²) имеет следующие значения: для воды +30, ртути - 10,1; спирта +11,5.

С явлением капиллярности приходится сталкиваться при исполь­зовании стеклянных трубок в приборах для измерения давления, а также в некоторых случаях истечения жидкости. Большое значе­ние приобретают силы поверхност­ного натяжения в жидкости, нахо­дящейся в условиях невесомости.

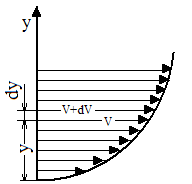
Рис.1.3 Течении вязкой жидкости вдоль твердой стенки

Д). Вязкость представляет собой свойство жидкости сопротивляться сдвигу (скольжению) ее слоев. Это свойство проявляется в том, что в жидкости при определенных усло­виях возникают касательные напря­жения. Вязкость есть свойство, противоположное текучести: более вязкие жидкости (глицерин, смазочные масла и др.) являются менее текучими, и наоборот.

При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью (рис. 1.3). Скорость v уменьшается по мере уменьшения расстояния у от стенки вплоть до v = 0 при у = 0, а между сдоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений (на­пряжений трения),

Согласно гипотезе, высказанной впервые Ньютоном в 1686 г., а затем экспериментально обоснованной проф. Н. П. Петровым в 1883 г., касательное напряжение в жидкости зависит от ее рода и характера течения и при слоистом течении изменяется прямо пропорционально так называемому поперечному градиенту скорости. Таким образом

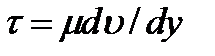(1.18)

где μ — коэффициент пропорциональности, получивший название динамиче­ской вязкости жидкости; dv — приращение скорости, соответствующее прира­щению координаты dy (см. рис. 1.3).

Поперечный градиент скорости dv/dy определяет изменение ско­рости, приходящееся на единицу длины в направлении нормали к стенке и, следовательно, характеризует интенсивность сдвига жидкости в данной точке (точнее dv/dy — это модуль градиента ско­рости; сам градиент — вектор).

Из закона трения (5.11), следует, что напряжения трения возможны только в движущейся жидкости, т. е. вязкость жидкости проявляется лишь при ее течении. В покоящейся жидкости касательные напряжения будем считать равными нулю *.

Изложенное позволяет сделать вывод, что трение в жидкостях, обусловленное вязкостью, подчинено закону, принципиально от­личному от закона трения твердых тел.

Если течение жидкости таково, что имеется еще градиент скоро­сти в направлении, нормальном к плоскости рисунка (см. рис. 1.2), то полную производную в формуле (5.11) надо заменить частной производной dv/dy.

При постоянстве касательного напряжения по поверхности S полная касательная сила (сила трения), действующая по этой по­верхности

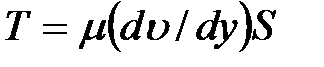(1.19)

Для определения размерности вязкости μ (Па*с) решим уравне­ние (5.11) относительно μ, в результате чего получим

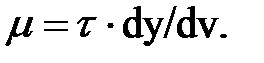
Наряду с динамической вязкостью μ применяют кинематическую:

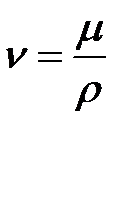(1.20)

Единицей измерения кинематической вязкости является стокc:
1 Ст = 1 см²/с. Сотая доля стокса называется сантистоксом (сСт).

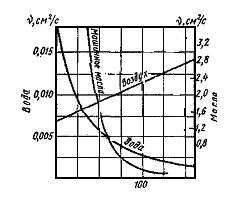
Вязкость капельных жидкостей зависит от температуры и умень­шается с увеличением последней (рис. 1.3). Вязкость газов, наоборот, с увеличением температуры возрастает. Объясняется это различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличе­нием температуры уменьшаются, поэтому вязкость падает, В газах же вязкость обусловлена, главным образом, беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повы­шением температуры. Поэтому вязкость газов с увеличением темпе­ратуры возрастает.

Влияние температуры на вязкость жидкостей можно оценить формулой

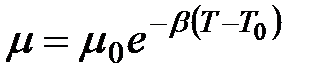(1.21)

где μ и μ₀ — вязкости при температуре Т и Т₀; β — коэффициент, значение которого для масел изменяется в пределах 0,02—0,03.

Рис. 1.4 Зависи­мость относительной вяз­кости μ/μ₀ от давления для предельных значений коэффициента α.

Вязкость жидкостей зависит также от давления, однако эта за­висимость существенно проявляется лишь при относительно боль­ших изменениях давле­ния (в несколько десятков МПа). С увеличением давления вязкость боль­шинства жидкостей растает, что может быть оценено формулой

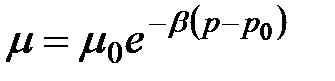
где μ и μ₀ — вязкости при давлении р и р₀, 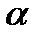- коэффициент, значение которого для минеральных масел изменяется в пределах 0,02-0,03 (нижний предел соответствует высоким температурам, а верхний - низким).

Приближенная зависи­мость относительной вяз­кости μ/μ₀ от давления для минеральных масел показана на (рис. 1.4) для предельных значений коэффициента α.

Вязкость жидкостей измеряют при помощи, вискозиметров. Наи­более распространенным является вискозиметр Энглера, который представляет собой цилиндрический сосуд диаметром 106 мм, с ко­роткой трубкой диаметром 2,8 мм, встроенной в дно. Время t истече­ния 200 см³ испытуемой жидкости из вискозиметра через эту трубку под действием силы тяжести, деленное на время t_вод истечения того же объема дистиллированной воды при 20° С выражает вязкость в гра­дусах Энглера: 1 °Е = t/t_вод, где t_вод = 51,6 с.

Для пересчета градусов Энглера в стоксы в случае минеральных масел применяют формулу

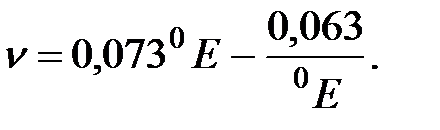
Ж). Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий, в которых они находятся.

Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном дав­лении; чем выше температура кипения, тем меньше испаряемость жидкости. В гидросистемах нормальное атмосферное давление явля­ется лишь частным случаем; обычно приходится иметь дело с испаре­нием, а иногда и кипением жидкостей в замкнутых объемах при раз­личных температурах и давлениях. Поэтому более полной характе­ристикой испаряемости является давление (упругость) насыщенных паров р_{н п}, выраженное в функции температуры. Чем больше дав­ление насыщенных паров при данной температуре, тем больше испа­ряемость жидкости. С увеличением температуры давление р_н.п увели­чивается, однако у разных жидкостей в разной степени.

Если для простой жидкости рассматриваемая зависимость явля­ется вполне определенной, то для сложных жидкостей, представля­ющих собой многокомпонентные смеси (например, для бензина и др.), давление />_н.п зависит не только от физико-химических свойств и температуры, но и от соотношения объемов жидкой и паровой фаз, Давление насыщенных паров возрастает с увеличением части объема, занятого жидкой фазой. Обычно значения упругости паров сложных жидкостей даются для отношения паровой и жидкой фаз, равного 4:1.

З). Растворимость газов в жидкостях характеризуется количе­ством растворенного газа в единице объема жидкости, различна для разных жидкостей и изменяется с увеличением давления.

Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо про­порциональным давлению, т. е.

,

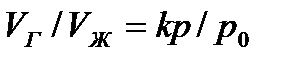где V_Г — объем растворенного газа, приведенный к нормальным условиям (p₀, T₀); V_Ж — объем жидкости; k — коэффициент растворимости; р — давление жидкости.

Коэффициент k имеет следующие значения при 20 °С: для воды 0,016, керосина 0,13, минеральных масел 0,08, жидкости АМГ-10 — 0,1.

При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказываться на работе гидросистем.

Гидростатика