Вираження теплоти і роботи через параметри стану
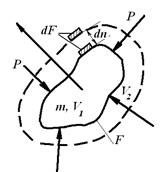
Розглянемо процес розширення газу масою m, поміщеного в еластичну оболонку поверхнею F, проти сил зовнішнього тиску. На початку розширення об'єм V1, в кінці - 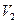 . При цьому елементарна площадка по нормалі до поверхні переміститься на відстань dn. Визначимо роботу газу. Елементарна робота dL=PdFdn=PdV, де . При цьому елементарна площадка по нормалі до поверхні переміститься на відстань dn. Визначимо роботу газу. Елементарна робота dL=PdFdn=PdV, де 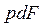 - сила, а dn - шлях. - сила, а dn - шлях.
| 
|
Повна робота 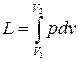 , питома робота
, питома робота  .
.
Припустимо, що процес розширення в координатах 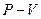 і T–S зображаються лінією 1-2.
і T–S зображаються лінією 1-2.

Відповідно до другого закону термодинаміки теплота визначається за формулою: 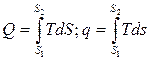 . У геометричному вираженні добуток pdV і TdS визначає елементарну площадку під нескінченно малою ділянкою процесу (заштрихована), тоді інтегрування показує, що площа під кривою процесу в
. У геометричному вираженні добуток pdV і TdS визначає елементарну площадку під нескінченно малою ділянкою процесу (заштрихована), тоді інтегрування показує, що площа під кривою процесу в 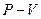 координатах дорівнює роботі L(l), а в
координатах дорівнює роботі L(l), а в 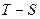 координатах - теплоті. Теплота і робота залежать від шляху протікання процесу, і не мають властивості повного диференціалу, тому інтегрування по замкненому контуру
координатах - теплоті. Теплота і робота залежать від шляху протікання процесу, і не мають властивості повного диференціалу, тому інтегрування по замкненому контуру 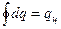 а
а 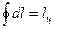 .
.
Теплоємність
Кількість теплоти, яку необхідно підвести (відвести до тіла), щоб змінити температуру на 10С, називається теплоємністю:
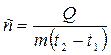 ,
,
де Q – кількість теплоти,
m – кількість речовини,
t1 і t2 – початкова і кінцева температури.
В залежності від одиниці кількості речовини, розрізняють питому теплоємність:
масову с, 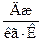 ; об'ємну
; об'ємну 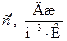 ; молярну
; молярну 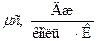 . Взаємозв’язок між ними: с’=сρ; μс=22,4с’.
. Взаємозв’язок між ними: с’=сρ; μс=22,4с’.
Якщо теплота підводиться у процесі з постійним тиском, то такі теплоємності називаються ізобарними: 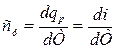 ; якщо в процесі з постійним об'ємом, то ізохорними:
; якщо в процесі з постійним об'ємом, то ізохорними:  .
.
Рівняння Майєра виражає зв'язок між ними: 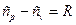 – для ідеального газу;
– для ідеального газу; 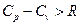 – для реального газу.
– для реального газу.
Якщо теплоємність визначається в межах якоїсь однієї температури, то така теплоємність називається істинною 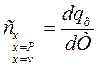 ; якщо її визначають в інтервалі температур, то теплоємність називають середньою
; якщо її визначають в інтервалі температур, то теплоємність називають середньою 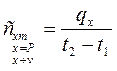 .
.
У відповідності з молекулярно-кінетичною теорією теплоємності, вона залежить від температури, тоді
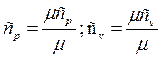 .
.
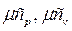 – молярні теплоємності, значення яких наводяться в довідниках в залежності від атомності газу. За квантовою теорією теплоємності, вона залежить від температури:
– молярні теплоємності, значення яких наводяться в довідниках в залежності від атомності газу. За квантовою теорією теплоємності, вона залежить від температури:
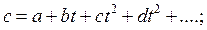
де а, b, с, d – постійні коефіцієнти, t – температура.
Перші два члени рівняння визначають лінійну залежність, а останні – нелінійну. Тоді середню теплоємність визначають: 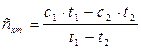 .
.
Дата добавления: 2020-02-05; просмотров: 1047;











