КІНЕМАТИЧНИЙ АНАЛІЗ МЕХАНІЗМІВ
6.1. ЗАДАЧІ КІНЕМАТИЧНОГО АНАЛІЗУ МЕХАНІЗМІВ
Основною задачею кінематики механізмів є вивчення руху ланок механізмів без врахування сил, що викликали цей рух.
Кінематичне дослідження механізму складається в основному у вирішенні трьох задач:
а) визначення переміщень ланок і траєкторій, описуваних точками ланок;
б) визначення швидкостей окремих точок ланок і кутових швидкостей ланок;
в) визначення прискорень окремих точок ланок і кутових прискорень ланок.
Якщо механізм має один ступінь вільності, то переміщення s, швидкість v, і прискорення a є функцією s, v, a однієї з ланок,прийнятої за початкову.
Якщо механізм має декілька ступенів вільності, то s, v, a є функціями відповідно s, v, a ланок механізму, прийнятих за початкові.При цьому число початкових ланок повинне дорівнювати числуступенів вільності (числу узагальнених координат).
6.2. ЗАКОНИ РУХУ ПОЧАТКОВИХ ЛАНОК
Розглянемо в якій формі можуть бути задані закони руху початкових ланок, надалі ці закони будемо називати функціями переміщень, швидкостей чи прискорень.
Функція переміщень може бути задана, наприклад, в аналітичній формі у вигляді функції зв'язку переміщення і часу.
Якщо початкова ланка входить в обертальну пару зі стояком (рис.5.1,а), то задається функція
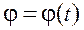 , (1)
, (1)
де, j - кут повороту початкової ланки відносно нерухомої системи координат. Якщо початкова ланка і стояк утворять поступальну пару (рис.1,б), то задається функція s = s(t).
Функції j=j(t) і s = s(t) можуть бути також задані графічно як криві. По осях ординат відкладені j чи s , а по осі абсцис - t у деяких обраних масштабах (рис.2).
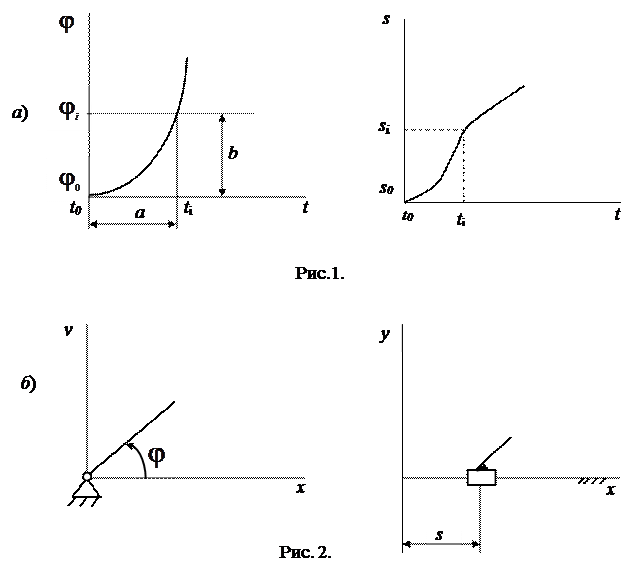
Час t за який початкова ланка повернулася на кут ji:
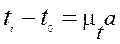 (2)
(2)
У деяких інженерних задачах закон руху початкової ланки може бути заданий як функція швидкостей ω = ω(t) чи v = v(t), тоді кут повороту чи переміщення початкової ланки можуть бути визначені за формулами:
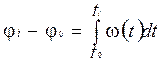 (3)
(3)
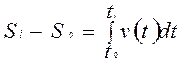
Якщо закон руху початкової ланки заданий як функція прискорення a = a(t), то перехід до функції швидкостей здійснюється шляхом обчислення інтегралів, формули (4), (5).
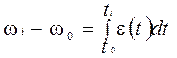 (4)
(4) 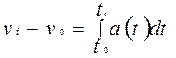 (5)
(5)
Дата добавления: 2016-06-15; просмотров: 1920;











