Примеры решения задач. Определить тип кривой и изобразить её в исходной системе координат

1. С помощью переноса начала координат привести уравнение кривой второго порядка к каноническому виду. Определить тип кривой и изобразить её в исходной системе координат:

4x² +z² –24x+8y+2z+5=0.

Решение. Выделим в уравнении полные квадраты:

4(x² –6x+ 9)–36 +(z² +2z+1) -1+8y+5=0,

4(x–3)² +(z+1)² +8y–32=0,

4(x–3)² +(z+1)² =–8(y–4).

Делаем замену координат:

x¢=x–3,

y¢=y–4,

z¢=z+1,

Она равносильна переносу начала координат в точку O'(3, 4,–1). После замены получаем уравнение

4x¢² +z¢² =–8y¢, Û(x¢)² +=–8y¢,

Это уравнение задает эллиптический параболоид, ось которого будет 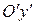. В сечении плоскостью 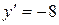получится эллипс +=1 с полуосями 4 и 8. Это следует учесть при изображении.

2. Определите, какое множество определяется в декартовой системе координат неравенством

(x–3)–4(y+4)² ³0.

Изобразите это множество.

Решение. Определим сначала, какое множество определяется уравнением (x–3)–4(y+4)² =0. Делаем замену координат

x¢=x–3,

y¢=y+4,

z¢=z.

Она равносильна переносу начала координат в точку O'(3,–4, 0). В новой системе координат 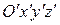получаем, что поверхность задается уравнением

(x¢)² –4(y¢)² =0. (*)

Поскольку в уравнении отсутствует координата z¢, то мы сразу делаем вывод, что наша поверхность является цилиндрической и ее образующие параллельны оси O¢z¢.На плоскости O¢x¢y¢ уравнение (*) задает пару пересекающихся прямых

(x¢–2y¢)(x¢+2y¢)=0.

Эта кривая 2 порядка будет направляющей для нашей поверхности. Значит, наша поверхность – это пара пересекающихся плоскостей. Для того, чтобы не загромождать изображение мы нарисовали только небольшую часть этой поверхности. Поскольку изначально у нас было неравенство, то искомое множество – это внутренность одной из двух пар вертикальных углов, образуемых этими плоскостями. Мы возьмем любую точку на оси O¢x¢: A(a,0,0)_O¢x¢y¢z¢ и убедимся, что ее координаты удовлетворяют неравенству (x¢)² –4(y¢)² ³0. Значит, ось O¢x¢ лежит в нашем множестве. Таким образом, исходное неравенство задает внутренность изображенного двугранного угла и угла, вертикального с ним. А т.к. неравенство нестрогое, то и сами плоскости тоже принадлежат множеству.

3. Составить уравнение поверхности, полученной вращением кривой

z=2y–2,

x=0.

вокруг оси a) Oz ,б) Oy. Определить тип поверхности. Изобразите ее.

Решение. Данная система уравнений задает прямую l , лежащую в плоскости Oyz. Первое из уравнений – это уравнение l в данной плоскости. Для того, чтобы составить уравнение поверхности Φ, получающейся вращением l вокруг Oz , мы должны в уравнении l оставить z без изменения, а y заменить на квадратный корень из суммы квадратов оставшихся координат: y a . Получаем уравнение

z=2–2, Þ

x²+y² –=0.

Данное уравнение определяет конус, ось которого – Oz , а вершина находится в точке O¢(0,0,–2).

Строим изображение данного конуса.

1) Подставив в уравнение конуса z=2, получим x²+y² =4. Значит, в сечении плоскостью z=2 получается окружность радиуса 2. Проводим через точку z=2 на оси Oz вспомогательные линии, параллельно осям Ox и Oy; откладываем на них от данной точки отрезки длины 2 и через получившиеся точки проводим эллипс, изображающий окружность. При этом, масштаб по оси Ox выбираем в два раза меньше, чем по осям Oy и Oz.

2) Строим эллипс равный данному с центром в точке z=–6 на оси Oz.

3) Проводим касательные к эллипсам через точку O¢. Подчеркнем, что точки касания ни в коем случае не совпадают с вершинами эллипса.

4) Часть нижнего эллипса, заключенную между точками касания изображаем пунктиром.

Аналогично, для того чтобы получить уравнение поверхности вращения вокруг Oy , мы в уравнении l оставляем y без изменения, а z заменяем: z a . Получаем уравнение

x² –4(y–1)² +z² =0,

–(y–1)² + = 0.

Оно задает конус, вершина которого находится в точке O¢(0,1,0) , а ось конуса – Oy. Эту поверхность тоже следует изобразить. При этом, учитываем, что в сечении плоскостью y =3 получается окружность радиуса 4.

4. Является ли поверхность заданная уравнением

– x² + + = 1

поверхностью вращения? Если да, то вращением какой кривой (написать уравнение) вокруг какой оси она получена? Изобразите ее.

Решение. Данная поверхность – это однополостной гиперболоид. В уравнении поверхности можно выделить выражение :

– x² + = 1,

и больше нигде в уравнении x и z не встречаются. Поэтому сразу делаем вывод, что это уравнение задает поверхность вращения вокруг Oy. Для того, чтобы определить, какая кривая g вращается, мы заменяем на y и получаем уравнение – x² + = 1 кривой, которая лежит в плоскости z=0. Для того, чтобы задать эту кривую в пространстве, мы должны написать систему уравнений

– x² + = 1

z=0

Можем заменить на z , и тогда получим уравнение кривой γ', лежащей в плоскости y=0:

–x² + = 1,

y=0.

5.Составьте уравнение поверхности, каждая точка которой равноудалена от плоскости x=– a и от точки F(a,0,0).

Решение. Пусть M(x,y) – произвольная точка поверхности. Тогда

|MF|= ,

а расстояние от M до плоскости равно |x+a|. По условию

= |x+a|.

Возводим это равенство в квадрат:

x²–2ax + a² +y²+z² = x²+2ax + a²

y²+z² = 4ax Û + = 2ax.

Это уравнение задает эллиптический параболоид, осью которого является Ox.

6.Найдите точки пересечения эллипсоида + +=1 и прямой = = .

Решение. Перепишем уравнение прямой в параметрическом виде:

x=1+t,

y= 4–6t,

z=–6+12t.

Подставим эти равенства в уравнение эллипсоида:

+ +=1,

1+2t+t² +4–12t+9t² +4–16t+16t² =9,

26t² –26t=0 Û 26t(t–1) =0.

Имеем два решения: t₁= 0, t₂= 1. Подставляя их в уравнение прямой, находим две точки M₁(1, 4,– 6), M₂(2, –2, 6).

Ответ: M₁(1, 4,– 6), M₂(2, –2, 6).

7. Определить, какая кривая получается в сечении поверхности + –=1 плоскостью а)y=2z; б)y=2z+2.

Решение. а)Данная поверхность – это однополостной гиперболоид. Подставим y=2z в уравнение поверхности:

+ –=1 Û x² =9.

Это уравнение проекции данной кривой на координатную плоскость Oxz. Оно задает пару параллельных прямых. Следовательно, наша кривая – это тоже пара параллельных прямых.

б)Подставим y=2z+4 в уравнение поверхности:

+ –=1 Û + =1 Û x² =9z.

Это уравнение проекции данной кривой на координатную плоскость Oxz. Оно задает параболу. Следовательно, наша кривая – это тоже парабола.

ПРИЛОЖЕНИЕ