Цилиндрические поверхности.

<29 30 313233 34 35 >

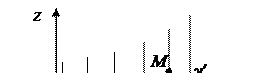Определение. Линейчатой называется поверхность, через каждую точку которой проходит хотя бы одна прямая, принадлежащая поверхности.

Определение. Цилиндрической называется поверхность, которую образует множество параллельных прямых (образующих), проходящих через каждую точку некоторой кривой (направляющей).

Пусть F – цилиндрическая поверхность. Выберем декартову СК так, чтобы ось Oz была параллельна

образующим. Если, при этом, направляющая g¢ не лежит в плоскости Oxy, то мы ее спроецируем в эту плоскость, и получим некоторую кривую g. Если теперь мы возьмем g в качестве направляющей, то получим ту же поверхность F. Поэтому будем с самого начала считать, что направляющей служит кривая g, лежащая в плоскости Oxy. Пусть

j(x,y)=0 – (1)

ее уравнение в плоскости Oxy (в пространстве она задается системой из двух уравнений: j(x,y)=0 и z =0). Пусть M(x,y,z) – произвольная точка поверхности F. Тогда ее проекция на плоскость Oxy будет точка M_o(x,y,0); и эта точка должна принадлежать кривой g. Поэтому ее координаты удовлетворяют (1). Но тогда этому уравнению будут удовлетворять и координаты точки M_o: ведь координаты x и y у этих точек одинаковы, а z в уравнение не входит.

Обратно, пусть координаты точки M(x,y, z) удовлетворяют (1). Тогда этому же уравнению удовлетворяют и координаты точки M_o(x,y,0), а т.к. M_oÎOxy, то M_oÎg. При этом, M и M_o лежат на одной прямой, параллельной оси Oz Þ MÎF.

Итак, мы установили, что (1) и есть уравнение поверхности F, т.е. уравнение цилиндрической поверхности совпадает с уравнением ее направляющей кривой g в плоскости Oxy, если образующие параллельны оси Oz. Аналогично, если образующие параллельны Oy, то уравнение цилиндрической поверхности совпадает с уравнением направляющей кривой в плоскости Oxz.

И обратно, если в уравнении поверхности отсутствует, например, координата x, то сразу можем сделать вывод, что эта поверхность цилиндрическая, а ее образующие параллельны Ox.

Пример. Пусть поверхность задана уравнением y²=2z . Тогда это цилиндрическая поверхность, ее образующие параллельны Ox, а направляющей служит парабола

y²=2z ,

x=0 .

Такая поверхность называется «параболический цилиндр».

Поскольку уравнение цилиндрической поверхности совпадает

с уравнением направляющей кривой, то список цилиндрических поверхностей второго порядка совпадает со списком их направляющих кривых второго порядка.

1. Эллиптический цилиндр	+ =1
2. Мнимый эллиптический цилиндр ( Æ )	+ =–1
3. Гиперболический цилиндр	– =1
4. Параболический цилиндр	y²=2pх
5. Пара пересекающихся плоскостей	a²x²–b² y²=0
6. Пара мнимых плоскостей, которые пересекаются по действительной прямой	a²x²+b² y²=0
7. Пара параллельных плоскостей	x²=a²
8. Пара совпадающих плоскостей	x²=0
9. Пара мнимых параллельных плоскостей ( Æ )	x²=–a²