Общее уравнение кривой второго порядка. Центр кривой.
Определение. Кривой второго порядка называется геометрическое место точек, координаты которых удовлетворяют уравнению
а11х2 + 2а12 ху + а22 у2 + 2а1х + 2а2у + с = 0, (8)
в котором хотя бы один из коэффициентов а11, а12, а22 отличен от нуля. Выражение
а11х2 + 2а12ху + а22 у2
называется квадратичной часть уравнения, 2а1х + 2а2у – линейной частью, а с – свободным членом.
Если мы перейдем к новой СК Ox¢y¢, то формулы замены координат будут иметь вид
 x = ax¢ + by¢ + b1,
x = ax¢ + by¢ + b1,
y = gx¢ + dy¢ + b2.
Если мы подставим эти выражения в (8), то снова получим уравнение такого же вида, т.е. содержащее x¢ и y¢ во второй степени. Поэтому наше определение корректно, т.е не зависит от выбора СК. В дальнейшем, СК всегда предполагается декартовой.
Определение. Точка O¢ называется центром кривой второго порядка, если она является ее центром симметрии. Кривая, которая имеет центр, называется центральной.
Предположим, что СК выбрана так, что ее начало находится в центре кривой. Тогда одновременно с точкой M(x, y) кривой будет принадлежать и точка M¢(– x,– y). Подставим ее координаты в (7) и получим
а11х2 + 2а12 ху + а22у2 – 2а1х – 2а2у + с = 0. (8¢)
Вычтем из равенства (8) равенство (8¢):
4(а1х + а2 у) = 0.
И это должно выполняться для любой точки M(x, y) на кривой. Поэтому а1 = а2 = 0, если начало координат находится в центре. Поэтому, если изначально начало координат не находится в центре O¢, то мы совершим параллельный перенос координатных осей в центр, и уравнение кривой в новой СК O¢х¢у¢ примет вид
а11х¢2 + 2а12 х¢у¢ + а22у¢2 + с¢ = 0, (9)
т.е. линейная часть уравнения исчезнет. При этом, коэффициенты квадратичной части останутся прежними; это будет установлено в процессе доказательства следующей теоремы.
Теорема 5. Координаты (xo, yo) центра кривой, заданной уравнением (8), находятся из системы линейных уравнений

 а11хo + а12 уo + а1 = 0,
а11хo + а12 уo + а1 = 0,
а12 хo + а22 уo + а2 = 0.
Доказательство. Введем новую декартову СК O¢х¢у¢, которая получается из Oху переносом начала в центр O¢(xo, yo) кривой. Тогда формулы замены координат имеют вид:

 x = x¢ + хo,
x = x¢ + хo,
y = y¢ + уo.
Подставим эти формулы в (7):
а11(x¢+ хo)2 + 2а12 (x¢+ хo)( y¢+ yo) + а22(y¢+ yo)2 +
+ 2а1(x¢+ хo) + 2а2(y¢+ yo) + с = 0.
После преобразований получаем
а11(x¢)2 + 2а12 x¢y¢+ а22(y¢)2 + 2(а11хo+ а12 уo+ а1)x¢+
+ 2(а12хo+ а22 уo+ а2)y¢+ с¢= 0,
где с¢ = j(xo, yo) – значение левой части уравнения (7) в точке O¢. Поскольку в новой СК коэффициенты при x¢ и y¢ должны быть равны нулю, то получаем (10).
 Заметим, что уравнение кривой в новой СК можно выписать, не совершая подстановки (11) и преобразований: коэффициенты квадратичной части не изменяются, надо только вычислить с¢.
Заметим, что уравнение кривой в новой СК можно выписать, не совершая подстановки (11) и преобразований: коэффициенты квадратичной части не изменяются, надо только вычислить с¢.


 Обозначим A = – матрица квадратичной части уравнения (8) (она же является матрицей системы линейных уравнений (10)),
Обозначим A = – матрица квадратичной части уравнения (8) (она же является матрицей системы линейных уравнений (10)),
d = det A, dx = – , dy = – .
1 случай. d ¹ 0. Тогда по правилу Крамера система (10) имеет единственное решение
xo= dx/d, yo= dy /d, (*)
а кривая имеет единственный центр. Минусы были поставлены выше потому, что а1 и а2 находятся в (10) не в правой части, а в левой.
2 случай. d = 0, dx¹ 0 и dy¹ 0 (заметим, что в случае d = 0, определители dx и dy будут равны или неравны нулю только одновременно). Тогда ранг расширенной матрицы системы (10) будет равен 2, а rank A=1. Значит, согласно теореме Кронекера-Капелли система (10) не имеет решений, а кривая не имеет центра.
3 случай. d = 0, dx = dy = 0. Тогда оба уравнения в (10) пропорциональны, а значит, эта система имеет бесконечное количество решений, а кривая – бесконечное количество центров.
Упростим еще величину с¢:
с¢ = j(xo, yo) = а11хo2 + 2а12 х oуo + а22 уo2 + 2а1хo + 2а2 уo + с =
= (а11хo + а12 уo + а1) хo+ (а12 хo + а22 уo + а2)уo + а12 хo + а22 уo + с.
В силу (9) выражения в скобках равны нулю, и мы имеем
с¢ = а1 хo + а2 уo + с. (12)
Подставляя сюда (*) получаем
с¢ = а1 + а2 + с = (а1dx + а2 dy + с) = , (13)
где

 а11 а12 а1
а11 а12 а1
D = а12 а22 а2 .
а1 а2 с
В скобках как раз стоит разложение D по последней строке или последнему столбцу. Равенство (13) позволяет выписать (9) не находя координат центра кривой. Но, если уже центр найден, то легче вычислить с¢ по формулам (12).
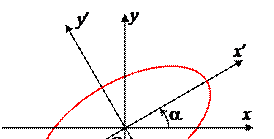 §8. Классификация центральных кривых второго порядка (случай d ¹ 0).
§8. Классификация центральных кривых второго порядка (случай d ¹ 0).
Попробуем дальше упростить уравнение (9). Выберем новую декартову СК O¢x²y², которая получается из O¢x¢y¢ поворотом координатных осей на некоторый угол a . Тогда формулы замены координат имеют вид:

 x¢ = x²·cos a – y²·sin a,
x¢ = x²·cos a – y²·sin a,
y¢ = x²·sin a + y²·cos a.
Подставим эти формулы в (9):
а11(x²·cos a – y²·sin a)2 + 2а12(x²·cos a – y²·sin a)(x²·sin a + y²·cos a) +
+ а22(x²·sin a + y²·cos a)2 + с¢ = 0,
Раскроем скобки и приведем подобные при одинаковых координатах. Тогда коэффициент x²y² будет равен
– а12sin2a + (а22 – а11)sin a·cos a + а12cos2a
Приравняем это выражение к нулю, и получившееся уравнение разделим на – cos2a :
а12 tg2a + (а11 – а22) tg a + а12 = 0. (15)
Это квадратное уравнение относительно неизвестного tg a, его дискриминант
D = (а11 – а22)2 + а12 ³ 0.
Значит, (14) всегда имеет решение, т.е всегда существует такой угол a, что в новой СК мы получим уравнение кривой без слагаемого, содержащего x²y². В результате наше уравнение будет иметь вид
l1(x²)2 + l2(y²)2 + = 0. (16)
Примем пока без доказательства, что коэффициенты l1 и l2 являются корнями уравнения

= 0 ;
в развернутом виде:
l2– sl + d = 0, (17)
где s = trace A = а11 – а22 – след матрицы A. Оно называется характеристическим уравнением кривой второго порядка. Согласно теореме Виета получаем
l1+ l2 = s , l1·l2 = d.
Относительно новой СК O¢x²y² получаем

A¢ = , d¢= det A¢= l1·l2 = d, s¢= trace A¢ = l1+l 2 = s,

 l1 0 0
l1 0 0
D¢ =0 l2 0 = l1·l2· (D/d) = D .
0 0 D/d
Таким образом, d¢= d , s¢= s, D¢ = D , т.е. величины d , s, D не изменяются при переходе к новой декартовой СК. Поэтому они называются инвариантами кривой второго порядка.
1 случай: D ¹ 0. Если опустить штрихи, то уравнение (16) можно переписать в виде
+ = 1. (18)
Обозначим a2 = |D/l1d|, b2 = |D/l2d|.
а) d > 0, sD < 0. Тогда l1·l2> 0 , т.е. l1 и l 2 одного знака, и (l1+ l 2)·D < 0, т.е. знак D противоположен знаку l1 и l 2. Поэтому оба знаменателя в (17) положительны, и уравнение (15) задает эллипс:
+ = 1 .
б) d > 0, sD > 0. Тогда оба знаменателя в (18) отрицательны, и уравнение имеет вид
+ = –1 .
Говорят, что оно задает мнимый эллипс. На действительной плоскости это пустое множество.
в) d < 0, D ¹ 0. Тогда l1 и l 2 имеют разные знаки, и поэтому знаменатели в (17) имеют разные знаки. Получаем уравнение
– = 1 или – = –1.
В любом случае получается уравнение гиперболы.
 2 случай: D = 0. В этом случае уравнение (15) принимает вид (штрихи опускаем):
2 случай: D = 0. В этом случае уравнение (15) принимает вид (штрихи опускаем):
l1x2 + l 2y2 = 0. (19)
Обозначим a2 =½l1½, b2 =½l2½.
а) d < 0. Тогда l1 и l 2 разного знака и (18) можно переписать в виде
a2x2 – b2 y2 = 0 Û
Û (ax – b y)·(ax + b y) = 0.
Этому уравнению удовлетворяют точки, для которых ax – by = 0 и точки для которых ax + by = 0 . Поэтому оно определяет пару прямых, очевидно, пересекающихся в центре O¢ и симметричных относительно координатных осей.
б) d > 0. Тогда l1 и l 2 имеют одинаковые знаки и (19) можно переписать в виде
a2x2+b2y2 = 0 Û (ax – i b y)·(ax + i b y) = 0.
(i – мнимая единица). Говорят, что это уравнение задает пару мнимых пересекающихся прямых. Но пересекаются они в действительной точке O¢ – центре кривой.
В случае d = D = 0 кривая тоже имеет центр (бесконечное количество центров), но этот случай мы рассмотрим в следующем параграфе.
§9. Классификация нецентральных кривых второго порядка (случай d = 0).
Пусть теперь d = 0. Тогда мы не можем использовать процедуру нахождения центра, и сразу совершаем поворот координатных осей на угол, тангенс которого находится из уравнения (14). Получим новую декартову СК с тем же началом Ox¢y¢. Формулы замены координат имеют вид
 x = x¢×cos a – y¢×sin a,
x = x¢×cos a – y¢×sin a,
y = x¢×sin a + y¢×cos a.
Здесь на один штрих с каждой стороны меньше, чем в (14), поскольку это первая замена координат. В этой СК уравнение кривой не будет включать слагаемое, содержащее произведение x¢y¢:
l1x¢2 + l 2 y¢2 + 2b1х¢ + 2b2 у¢ + с = 0, (20)
Заметим, что коэффициент с останется прежним, а непосредственное вычисление показывает, что
b1= a1×cos a + a2×sin a, b2 = a1×sin a + a2×cos a.
Числа l1 и l 2 можно найти из уравнения (17). Так как d = l1·l2 = 0, то один из корней будет равен нулю. Пусть это будет l1. Имеем уравнение
l 2 y¢2 + 2b1х¢ + 2b2 у¢ + с = 0. (21)
Для этого уравнения

 0 0 b1
0 0 b1
D = 0 l2 b2 = – l2b12.
b1 b2 с
1 случай: D = 0 Û b1= 0. Уравнение имеет вид l 2 y¢2 + 2b2 у¢ + с = 0. Выделим полный квадрат:
l 2( y¢ 2 + у¢ + ) – + с = 0 Û l 2( y¢ + )2– + с = 0 .
Обозначим с¢= (b12- l 2с) /l 2, a2 =½ с¢½ и сделаем замену координат:
 x²= x¢ ,
x²= x¢ ,
y²= y¢ + ,
которая равносильна переносу начала координат в точку O¢(0,– b1/l2)Ox¢y¢(подчеркнем, что координаты указаны в промежуточной СК Ox¢y¢). Получим уравнение
(y²)2 = a2.
а) с¢ > 0 Þ (y²)2 = a2, т.е. y² = a или y² =– a . Наша кривая – это пара параллельных прямых.
б) с¢ > 0 Þ (y²)2 =– a2, т.е. y² = i a или y² =– i a . Говорят, что наше уравнение задает пару мнимых параллельных прямых.
в) с¢ = 0 Þ (y²)2 =0. Говорят, что это уравнение задает пару совпадающих прямых.
2 случай: D ¹ 0 Û b1¹ 0. Так же, как и в предыдущем случае, выделяем в (21) полный квадрат по y:
l 22– + 2b1х¢ + с = 0 ,
а затем преобразуем так:
l 22+ 2b1 = 0 .
Обозначим c¢ = и сделаем замену координат:
 x²= х¢ – c¢ ,
x²= х¢ – c¢ ,
y²= y¢ + ,
которая равносильна переносу начала координат в точку O¢Ox¢y¢. Получим уравнение
l 2(y²)2 + 2b1х² = 0 Û (y²)2 = 2pх²,
где p = – 2b1/l 2 . Это уравнение задает параболу.
Итак, мы установили, что общее уравнение кривой второго порядка (8) задает одну из следующих кривых второго порядка (sign x означает знак числа x).
| sign d | sign s·D | Кривая и ее каноническое уравнение | Кол-во центров |
| + | – | Эллипс + = 1 | |
| + | + | Мнимый эллипс + = –1 | |
| – | ± | Гипербола – = 1 | |
| – | Пара пересекающихся прямых | a2x2 – b2 y2 = 0 | |
| + | Пара мнимых пересекающихся прямых | a2x2 + b2 y2 = 0 | |
| ± | Парабола y2 = 2pх, | ||
| Пара параллельных прямых x2 = a2 Пара мнимых параллельных прямых x2 = – a2 Пара совпадающих прямых x2 = 0 | ¥ |
Дата добавления: 2020-02-05; просмотров: 776;











