ОБЩАЯ ХАРАКТЕРИСТИКА ЯЗЫКОВ ПРОГРАММИРОВАНИЯ
Разработка системного и прикладного программного обеспечения на персональных компьютерах осуществляется с помощью инструментальных средств, к которым в первую очередь относятся:
· трансляторы с языков высокого уровня;
· средства редактирования, компоновки и загрузки программ;
· макроассемблеры (машинно-ориентированные языки);
· отладчики машинных программ.
Основные инструментальные языки высокого уровня, используемые на персональных компьютерах - Basic, Pascal, C и др. Не вдаваясь в детальные описания указанных языков, рассмотрим кратко их основные свойства.
Basic
Исторически одним из самых популярных языков высокого уровня стал Basic. В чем причина этой популярности? Прежде всего Basic очень прост в освоении и использовании.
Режим интерпретации способствует сокращению характерного цикла в работе программиста: составлению программы - пробное использование - исправление ошибок - повторное исполнение. Это очень удобно при разработке небольших программ. Интерпретация, однако, имеет неизбежный недостаток - программа работает существенно медленнее, чем в случае использования трансляторов компилирующего типа, как, например, для языков Pascal и С. Объясняется это тем, что в режиме интерпретации каждый оператор языка сначала читается системой, анализируется в контексте уже работающей программы и лишь после этого исполняется. В трансляторах компилирующего типа, в отличие от этого, все стадии чтения и анализа осуществляется заранее - на этапе компиляции, а при исполнении работает готовая программа. Чтобы сохранить преимущества языка Basic и в то же время дать возможность построения эффективных, быстро работающих программ, созданы Basic-компиляторы. При этом на этапе составления и отладки программы используются преимущества интерпретационного режима, а после завершения отладки программа компилируется. Появления компилятора поставило Basic в один ряд с другими языками высокого уровня и придало ему дополнительную популярность.
Как правило, начинающие программисты пользуются этим языком для составления свои первых программ. Basic отводится ведущая роль в школьном образовании, как языку обучения основам программирования.
Языки Pascal и C
Языки Pascal и С чаще всего используются профессиональными системными программистами для разработки системных и прикладных программ. Оба эти языка позволяют позволяют работать с данными сложной структуры; оба имеют развитые средства для выделения отдельных частей программ в процедуры. Трансляторы этих языков работают в режиме компиляции, что позволяется создавать эффективные программы. Важным средством для построения больших программных систем является модульность, т.е. возможность независимой разработки отдельных частей программ и последующего их связывания в единую систему. Все эти особенности способствовали тому , что именно на Pascal и С разрабатывается большинство крупных программных систем.
Следует отметить, что между указанными языками, не смотря на общее сходство, имеются существенные различия. Pascal является классическим языком программирования, который приобрел популярность как отличный инструмент для решения серьезных задач. Программирование на Pascal обеспечивает высокую степень надежности программ.
Pascal, наряду с Basic, считается также учебным языком; он принят во многих учебных заведениях как базовый язык для изучения программирования.
Язык С в отличии от Pascal с момента появления был ориентирован на разработку системных программ. Он, в частности, послужил главным инструментом для создания операционных систем ЮНИКС и MS-DOS. В этом языке имеются более гибкие средства для эффективного использования особенностей аппаратуры, чем в Pascal. С другой стороны, синтаксис языка С менее прозрачен, чем у Pascal; возможностей для внесения ошибок больше; чтение текстовых программ требует определенного навыка. В связи с этим язык С применяется главным образом для создания системных и прикладных программ, в которых скорость работы и объем памяти являются критическими параметрами
2. ОСНОВЫ ПРОГРАММИРОВАНИЯ НА ЯЗЫКЕ
TURBO PASCAL
2.1. Оператор присваивания
Общий вид оператора присваивания:
<имя переменной>:=<выражение>
В зависимости от типа переменной бывают математический, логический, символьный, строковый и др. операторы присваивания. В данной главе подробно будет рассмотрен математический оператор присваивания. Выражение в правой части оператора может представлять собой константу (a=4E-3), имя переменной (d:=x) или математическое выражение, записываемое по следующим правилам:
1. Математическое выражение может состоять из констант, имен переменных и стандартных математических функций, соединенных знаками арифметических операций: "+", "-", "*", "/" (Табл. 2.1.1, пример 1). Как и в математике низший приоритет имеют (т.е. выполняются в последнюю очередь) операции "+" и "-", более высокий "*" и "/" и наивысший - вызов функции. Для повышения приоритета операции используются скобки (в Паскале при записи математического выражения используются только круглые скобки (Табл. 2.1.1, пример 2).
2. Если выражение представляет собой дробь, то оно «вытягивается в строчку», т.е. сначала записывается числитель, затем знак "/" затем знаменатель. (Табл. 2.1.1, пример 3). Если в числителе (или знаменателе) дроби стоит сумма (или разность), то т.к. операции "+" и "-" имеют более низкий приоритет, чем "/", то числитель (или знаменатель) заключаются в скобки. (Табл. 2.1.1, пример 4). Т.к. расчет выражения осуществляется слева направо, нет необходимости заключать в скобки произведение (частное), находящееся в числителе, но если оно стоит в знаменателе, то скобки ставить необходимо (Табл. 2.1.1, пример 5).
3. Для вычисления функций в Паскале имеется набор стандартных математических функций (см. табл. 2.1.2). Для вызова функции пишется ее имя и затем аргумент в круглых скобках. (Табл. 2.1.1, пример 6). Если функция не является стандартной, необходимо выразить ее через стандартные математические функции (см. табл. 2.1.3). (Табл. 2.1.1, пример 7).
Пример 2.1.1. Записать оператор присваивания.
а) 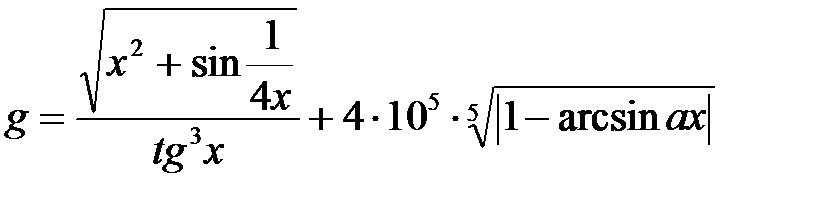
g:=sqrt(sqr(x)+sin(1/(4*x)))/exp(3*ln(sin(x)/cos(x)))+
4e5*exp(1/5*ln(abs(1-sqrt(x/(1-sqr(x)))));
б) 
x:=(1+2*exp(sin(x)*ln(x)))/(ln(a/x)/ln(10))-exp(-x*sqr(x)).
Таблица 2.1.1
Запись математических выражений на Паскале
| Математическая запись | Запись оператора на языке Паскаль |
| Арифметические выражения | |
1. 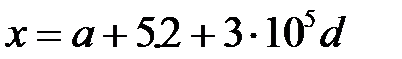
| x:=a+5.2–3E5*d; |
2. 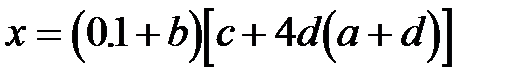
| x:=(0.1+b)*(c+4*d*(a+d)); |
3. 
| x:=3.5/a; |
4. 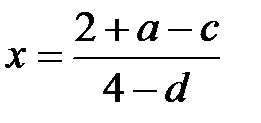
| x:=(2+a+c)/(4–d); |
5.а. 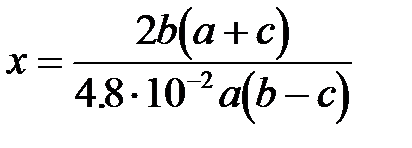
| x :=2*b*(a+c)/(4.8E-2*a*(b-c)); или x:=2*b*(a+c)/4.8E-2/a/(b-c); |
5.б. 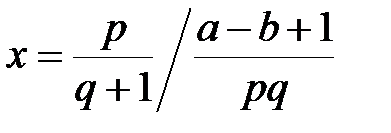
| x:=p/(q+1)/((a–b+1)/(p*q))или x:=p*(p*q)/(q+1)/(a–b+1) |
| Использование стандартных математических функций | |
6.a. 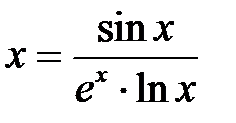
| x := sin(x)/(exp(x)*ln(x)); |
6.б. 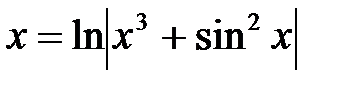
| x:=ln(x*sqr(x)+sqr(sin(x))) |
7. 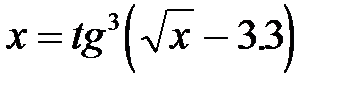
| x:=exp(3*ln(sin(sqrt(x)-3.3)/cos(sqrt(x)-3.3))) или a:=sqrt(x)-3.3;x:=exp(3*ln(sin(a)/cos(a))) |
Таблица 2.1.2
Стандартные математические функции
| x2 | sqr(x) | Вторая степень х |
| ex | exp(x) | Экспанента х |
| Sin x | sin(x) | Синус х |
| Arctg x | arctan(x) | Арктангенс х |

| sqrt(x) | Квадратный корень х |
| ln x | ln(x) | Натуральный логарифм х |
Продолжение табл. 2.1.2.
| cos x | cos(x) | Косинус х |
| [x] | int(x) или trunc(x) | Целая часть числа (для x>0). |
| {x} | frac(x) | Дробная часть числа. |
| round(x) | Округление до целого. | |
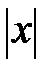
| abs(x) | Модуль числа |
Таблица 2.1.3
Расчет некоторых нестандартных математических функций
1. Тригонометрические функции
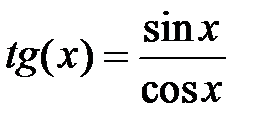 ,
, 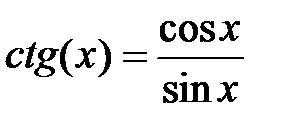 ,
, 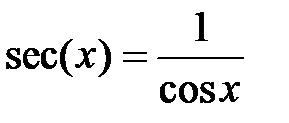 ,
, 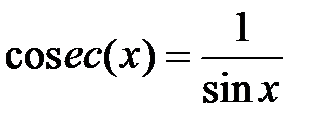 .
.
2. Обратные тригонометрические функции
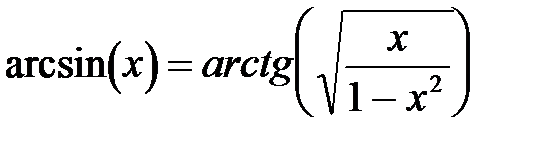 ,
, 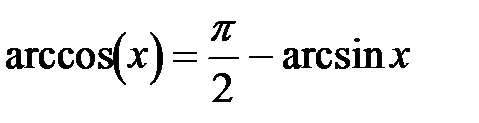 .
.
3. Возведение в степень
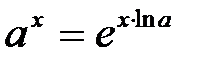 ,
, 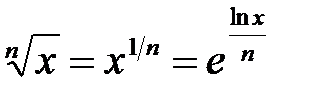 .
.
4. Расчет логарифмов
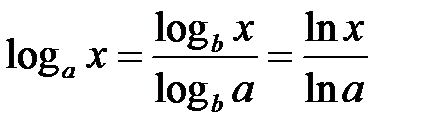 ,
, 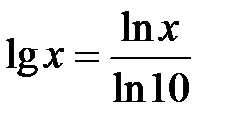 .
.
5. Гиперболические функции
а) гиперболический синус 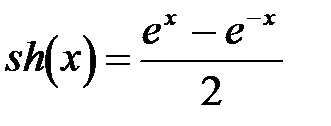 ,
,
б) гиперболический косинус 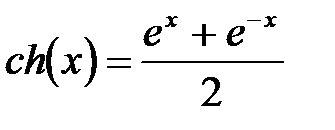 ,
,
в) гиперболический тангенс 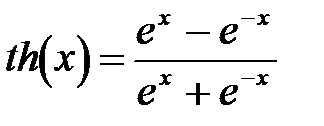 .
.
6. Обратные гиперболические функции
а) ареасинус 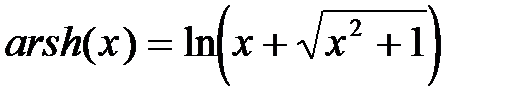 ,
,
б) ареакосинус 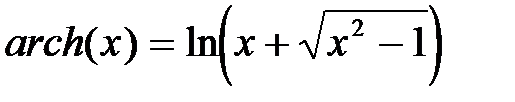 ,
,
в) ареатангенс 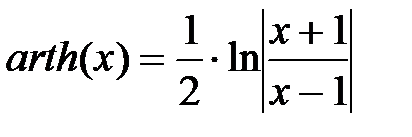 .
.
2.2. Программирование линейных алгоритмов
В данном разделе представлены примеры программ, в основе которых лежит алгоритм линейной структуры, т.е. алгоритм, в котором действия выполняются последовательно друг за другом без разветвлений. Обычно в задачах такого типа первое действие - ввод исходных данных, затем следуют необходимые расчеты, и в заключении - вывод результатов. Примеры оформления ввода и вывода данных приведены в
табл. 2.2.1.
Пример 2.2.1. Составить программу определения площади и объема сферы.
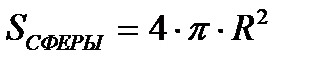
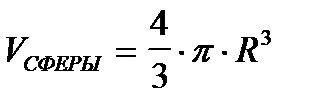 .
.
VARR, S, V:real;
BEGIN
{Ввод исходных данных}
write(’Введите радиус сферы R=’); readln(R);
{Расчет площади и объема сферы}
S:=4*Pi*sqr(R);
V:=4/3*Pi*exp(3*ln(R));
{Вывод результатов}
writeln(’Площадь сферы, S=’,S:12);
writeln(’Объем сферы, V=’,V:12);
END.
Пример 2.2.2. Рассчитать давление углекислого газа, предположив, что его поведение подчиняется уравнению Редлиха – Квонга:
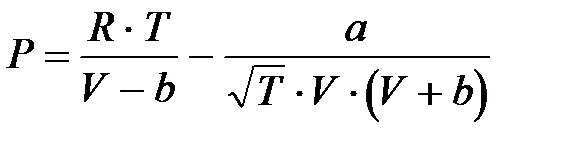 ,
,
если известны температура газа T (K) и занимаемый им объем V (м3). Параметры a и b определяются по формулам:
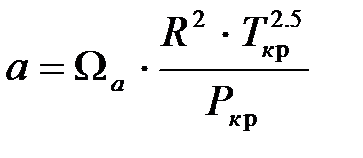 ;
; 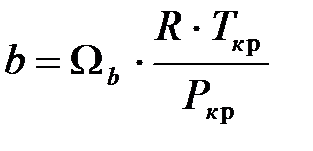 ,
,
где Ткр(К) и Ркр(Па) – критические температура и давление.
Wa=0.4274802327, Wb=0.08664035.
CONST
{Описание констант}
R=8.314;
Sa=0.4274802327;
Sb=0.08664035;
Tk=31.0 + 273.15;
Pk=7.39 * 101325;
VART, V, P, a, b:real;
BEGIN
writeln(’Введите значения температуры (Т) и объема (V)’);
readln (T,V);
a:=Sa*sqr(R)*exp(2.5*ln(Tk))/Pk;
b:=Sb*R*Tk/Pk;
P:=R*T/(V-b)-a/(sqrt(T)*T*(V+b));
writeln(’Давление газа равно P=’, P:7:0);
END.
Таблица 2.2.1
Примеры оформления ввода данных с клавиатуры и
вывода результатов на экран.
(Переменные a,b,c,x - типа real, а i - integer)
| Операторы | Вид на экране |
| Ввод данных | |
| 1. Ввод одной или нескольких переменных без пояснения | |
| Readln(a); Readln(a,c,x); | 2.3_ 2.3 4.6E-3 4_ |
| 2. Ввод одной переменной с пояснением в строчку | |
| Write(‘Imin=’); Readln(Imin); | Imin=27_ |
| 3. Ввод нескольких переменных в строчку | |
| Write(‘Введите a,b,c: ’); Readln(a,b,c); | Введите a,b,c: 8 3.123 4.44_ |
| 4. Ввод нескольких переменных в столбик | |
| Writeln(‘ a b c’); Readln(a,b,c); | a b c 8 3.765 2E-4_ |
| Вывод данных | |
| 1. Вывод одной переменной | |
| Writeln(‘a=’,a:6:3) | a=-34.284 |
| 2. Вывод нескольких переменных в строчку | |
| Writeln(‘a=’,a:6:3,’ b=’,b:10,’ i=’,i:3); | a=-34.284 b= 1.063E+02 i=127 |
| 3. Вывод нескольких переменных в столбик | |
| Writeln(‘a=’,a:6:3); Writeln(‘b=’,b:10); Writeln(‘i=’,i:3); | a=-34.284 b= 1.063E+02 i=127 |
Продолжение табл. 2.2.1.
| 4. Вывод нескольких переменных в виде таблицы с заголовком | |
| Writeln(‘ a b i’); Writeln((a:6:3,’ ‘,b:10,’ ‘,i:3); | a b i -34.284 1.063E+02 127 |
2.3. Программирование разветвляющихся алгоритмов.
Условный оператор
Алгоритм, в котором выполнение того или иного действия зависит от выполнения некоторого условия, называется разветвляющимся. Для программирования разветвляющихся алгоритмов в Паскале используется условный оператор.
Условный оператор используется в тех случаях, когда выполнение следующего действия в программе зависит от результатов предыдущих вычислений. Для записи условного оператора используются следующие служебные слова: IF, THEN, ELSE.
Общий вид условного оператора IF A THEN B; где A - логическое отношение , B - оператор, простой или составной. Для записи условного оператора перехода используются следующие логические отношения: = равно; < > не равно; < меньше; > больше; >= больше или равно; <= меньше или равно. Рассмотрим следующий условный оператор:
IF A < > 0 THEN B:=X/A;
В результате выполнения данного условного оператора В примет значение X/A только в том случае, если A не равно 0. Если A=0, то оператор присваивания B:=X/A; выполнен не будет.
Условный оператор может быть записан в следующем виде: IF A THEN ST1 ELSE ST2; где А - логическое отношение, а ST1 и ST2 - некоторые операторы. Если логическое отношение А - истина, то выполняется оператор ST1. Если логическое отношение A - ложь, то выполняется оператор ST2.
Пример 2.3.1
PROGRAM VVOD;
VAR n, C, d, b, g:real;
BEGIN write('введи n= ');read(n); c:=n+LN(N)+1;b:=c+1;
IF c < > 0 THEN IF b< > 10 THEN d:=1 ELSE d:=12.;g:=3;
writeln(C, d, g);
END.
Составной оператор. Если при некотором условии нужно выполнить последовательность операторов, то их объединяют в один составной оператор. Составной оператор начинается ключевым словом BEGIN и заканчивается ключевым словом END. Между этими словами помещаются составляющие операторы, которые выполняются в порядке их следования.
Рассмотрим пример составного условного оператора.
Пример 2.3.2
y=Cos 2x/5 при 5<=x<=10, r=sin 2x/10,
f= y+r; f=2.8 eX при x<5 или x>10.
PROGRAM FUNK;
VAR x, y, r, f:real;
BEGIN write('введи x= ');read(x);
IF (x<=10) and (x>=5) THEN BEGIN
y:=Cos(2.0*x)/5.0; r:=Sin(2*x)/10.0;
f:=y+r; END ELSE
f:=2.8*exp(x);
write('значение f',f);
END.
Виды разветвляющихся алгоритмов и способы программирования приведены в табл. 2.3.1. и 2.3.2.
Пример 2.3.3. Составить программу для решения квадратного уравнения.
VARA, B, C, X, X1, X2, D:real;
BEGIN
{Ввод коэффициентов a,b,c.}
writeln(’Данная программа решает квадратные уравнения типа :’);
writeln(’ A*X*X + B*X + C = 0 ’)
write(’Введите коэффициент А = ’); readln(A);
write(’Введите коэффициент B = ’); readln(B);
write(’Введите коэффициент C = ’); readln(C);
{Расчет дискриминанта}
D:=sqr(B)-4*A*C;
{Расчет корней.}
IF D < 0 THEN
BEGIN
writeln(’Данное уравнение вещественных корней’);
writeln(’НЕ ИМЕЕТ’);
END;
IF D = 0 THEN
BEGIN
X:=-B/(2*A);
writeln(’Данное уравнение имеет ОДИН вещественный корень’);
writeln(’ X = ’,X:10:6);
END;
IF D > 0 THEN
BEGIN
X1 := (-B+sqrt(D))/(2*A);
X2 := (-B-sqrt(D))/(2*A);
writeln(’Данное уравнение имеет ДВА вещественных корня’);
writeln(’ X1 = ’,X1:10:6,’ X2 = ’,X2:10:6);
END;
END.
Пример 2.3.4. Составить программу вычисления теплового эффекта химической реакции, если теплоемкость зависит от температуры.
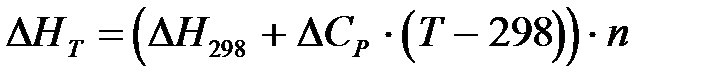 ,
,
где n=7.3 моль - количество вещества,
DH298=63 200 Дж/моль - мольный эффект реакции при стандартных условиях.
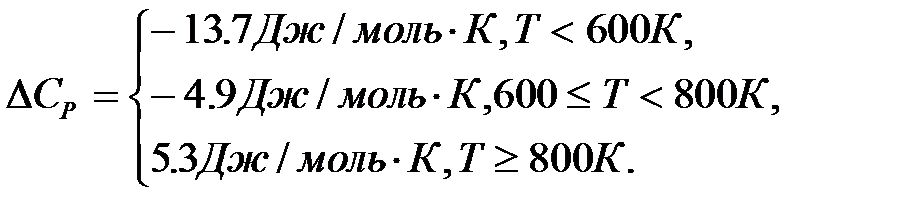
CONST
n=7.3; H298=63200; T1=600;T2=800;
Cp1= -13.7; Cp2= -4.9; Cp3=5.3;
VART, Cp, H:real;
BEGIN
write(’Введите температуру, К : T = ’); readln(T);
IF T < T1 THENCp:= Cp1 ELSE
IFT < T2 THEN Cp:= Cp2 ELSE Cp:= Cp3;
H:=(H298+Cp*(T-298))*n;
writeln(’Тепловой эффект : H=’, H:6:3);
END.
Пример 2.3.5. Вводятся значения длин трех отрезков. Составить программу определения возможности образования этими отрезками треугольника.
VARa, b, c: real;
BEGIN
write(’Введите длину первого отрезка a=’); readln(a);
write(’Введите длину второго отрезка b=’); readln(b);
write(’Введите длину третьего отрезка c=’); readln(c);
IF (a<=0) OR (b<=0) OR (c<=0) THENwriteln(’Вы неправильно ввели значения длин !’) ELSE
IF (a+b>c) AND (a+c>b) AND (b+c>a) THENwriteln(’Из этих отрезков МОЖЕТ быть образован треугольник !’) ELSEwriteln(’Из этих отрезков НЕ МОЖЕТ быть образован треугольник !’);
END.
Таблица 2.3.1
Виды разветвляющихся алгоритмов и способы их программирования
| Фрагмент блок – схема | Фрагмент программы |
| а) Разветвление.
| IF x>3 THEN y:=sqr(x-1) ELSE BEGIN z:=1/x; y:=exp(-z) END; |
| б) Обход. (1-й случай).
| IF (x>3) AND (c<2) THEN d:=c+x; |
Продолжение табл. 2.3.1.
| в) Обход. (2-й случай).
| Варианты программирования. 1) IF NOT (2*a>1) THEN writeln(’d=’,d:10); 2) IF 2*a<=1 THEN writeln(’d=’,d:10); 3) IF 2*a>1 THEN ELSEwriteln(’d=’,d:10); 4) IF 2*a>1 THEN GOTO1; writeln(’d=’,d:10); 1:…… |
Два способа расчета функции с условиями (Таблица 2.3.2):
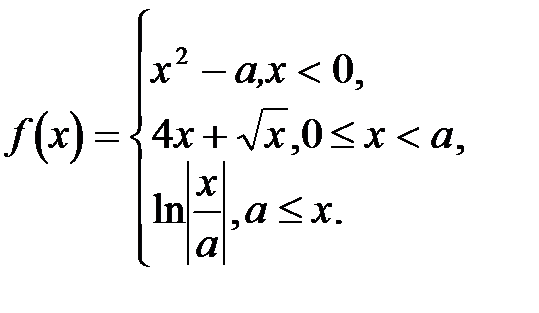
Таблица 2.3.2
| Способ 1 | Способ 2 |
| . . . IF x<0 THEN f:=sqr(x)-a ELSE IF x<a THEN f:=4*x+sqrt(x) ELSE f:=ln(abs(x/a)); . . . | . . . IF x<0 THEN f:=sqr(x)-a; IF (0<=x) AND (x<a) THEN f:=4*x+sqrt(x); IF a<=x THEN f:=ln(abs(x/a)); . . . |
2.4. Оператор варианта
Оператор варианта (CASE ... OF) предназначен для программирования алгоритмов с множественным выбором.
Пример 2.4.1. Составить программу для вывода названий месяцев по их номеру.
VARN:integer;
BEGIN
write(’Введите номер месяца : ’); readln(N);
CASE N OF
1: writeln(’ ЯНВАРЬ’);
2: writeln(’ ФЕВРАЛЬ’);
3: writeln(’ МАРТ’);
4: writeln(’ АПРЕЛЬ’);
5: writeln(’ МАЙ’);
6: writeln(’ ИЮНЬ’);
7: writeln(’ ИЮЛЬ’);
8: writeln(’ АВГУСТ’);
9: writeln(’ СЕНТЯБРЬ’);
10: writeln(’ ОКТЯБРЬ’);
11: writeln(’ НОЯБРЬ’);
12: writeln(’ ДЕКАБРЬ’);
ELSE writeln(’Вы неправильно ввели номер месяца ! ’);
END.
Пример 2.4.2. Составить программу вычисления сумм арифметической и геометрической прогрессий, а также определения значения заданного члена прогрессии.
Для арифметической прогрессии:
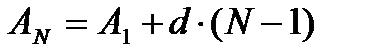
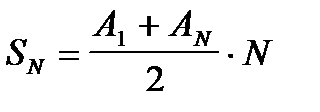
Для геометрической прогрессии:
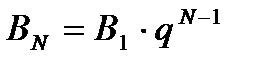
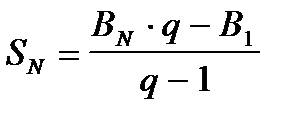
VARV, N:integer;
A1, B1, AN, BN, SA, SB, d, q:real;
BEGIN
writeln(’Выберите вид прогрессии : ’);
writeln(’ 1- арифметическая’);
writeln(’ 2- геометрическая’);
readln(V);
CASE V OF
1: BEGIN
writeln(’Вы выбрали арифметическую прогрессию.’);
write(’Введите первый член прогрессии A1 =’); readln(A1);
write(’Введите разность прогрессии d =’); readln(d);
write(’Введите номер N =’); readln(N);
AN:=A1+d*(N-1);
SA:=(A1+AN)*N/2;
writeln(N, ’-й член прогрессии равен =’,AN:6:3);
writeln(’Сумма первых ’,N,’ членов прогрессии равна =’,SA:6:3);
END;
2: BEGIN
writeln(’Вы выбрали геометрическую прогрессию.’);
write(’Введите первый член прогрессии B1 =’); readln(B1);
write(’Введите знаменатель прогрессии q =’); readln(q);
write(’Введите номер N =’); readln(N);
BN:=B1*exp((N-1)*ln(q));
SB:=(BN*q-B1)/(q-1);
writeln(N, ’-й член прогрессии равен =’,BN:6:3);
writeln(’Сумма первых ’,N,’ членов прогрессии равна =’,SB:6:3);
END;
END.
2.5. Программирование циклических алгоритмов
Алгоритмы, в которых действия повторяются многократно, называются циклическими. Виды циклических алгоритмов и способы их программирования приведены в табл. 2.5.1. Часто используются циклы для расчета сумм, произведений, количества. Виды сумм и способы их расчета приведены в табл. 2.5.2. Примеры программ с циклическими алгоритмами приведены также в следующих разделах: 6, 7, 8.
В языке Паскаль существуют три оператора цикла:FOR … TO … DO, WHILE … DO, REPEAT … UNTIL.
Общий вид оператора WHILE A DO ST, где А – логическое выражение, ST – оператор, простой или составной.
WHILE X< >0 DO BEGIN G:= C+1/X; x:=x-1 END; В данном примере вычисляется логическое выражение типа X< >0.
Если оно «истина», то будут выполняться операторы G:= 1/X; X:=X-1; и управление опять будет передаваться вновь на проверку выражения X< >0. Как только условие X<>0, будет «ложь», будет выполняться оператор, следующий за END. То есть цикл повторяется пока
X< >0.
Оператор цикла FOR:
FOR i:=n1 TO n2 DO ST;
где i - переменная цикла; n1 - конечное значение переменной; n2 - конечное значение переменой ST - оператор, простой или составной.
FOR i:= 1 TO 20 DO a:=a+1; При такой записи будет выполняться оператор A:=A+1; пока i поочередно принимает значения i= 1,2,...,20.
В операторе FOR шаг изменения параметра цикла равен 1, однако имеется разновидность цикла For или цикл по убывающим значениям параметра цикла,в этом случае параметр цикла изменяет свое значение с шагом -1 от N2 до N1 : FORI:= n2 DOWNTO n1 DO ST; , FOR i:= 20 DOWNTO n2 DO A:=A+1;
Оператор с постпроверкой условия имеет следующий вид: REPEAT ... UNTIL, где REPEAT < операторы > UNTIL < условие >. Операторы выполняются хотя бы один раз, после чего вычисляется условие. Если значение условия есть FALSE, операторы повторяются, в противном случае оператор завершает свою работу.
Однако цикл может быть организован с помощью условного оператора и оператора безусловного перехода. Метки. Для указания последовательности выполнения программ используют метки. Метка может состоять из букв и цифр, но первой должна стоять буква. В качестве исключения метка может состоять только из цифр, в диапазоне от 0 до 9999. Все метки, используемые в программе, должны быть обозначены с помощью служебного слова LABEL. (Например, label c1,c2;).
Оператор безусловного перехода имеет следующий общий вид:
GOTO N,
где N – имя метки; GOTO - служебное слово.
Метка N описывается с помощью служебного слова LABEL и ставится перед следующим оператором, который должен быть выполнен.
Пример 2.5.1.
PROGRAM Met;
LABEL d1;
VAR p, y, x:real;
BEGIN
read(p);
GOTO d1;
Y:=ln(p)+1;
d1:X:= sqr(p);
write(x);
END.
В результате выполнения данной программы будет вычислена величина X. Значение У останется незаданным, так как управление в программе передается на оператор с меткой d1.
Пример 2.5.2. Составить программу для определения гидравлического сопротивления слоя насадки при изменении скорости газа от 10 до 15 м/с с шагом h=0.5 м/с.
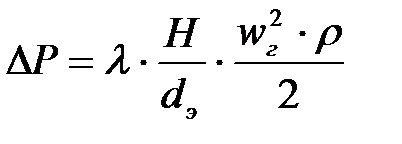
где H - высота слоя, м,
dэ - эквивалентный диаметр, м,
r - плотность газа, кг/м3,
wг - скорость газа, м/с.
Коэффициент гидравлического сопротивления рассчитывается по формуле:
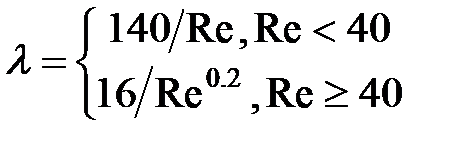
где Re - критерий Рейнольдса – равен:
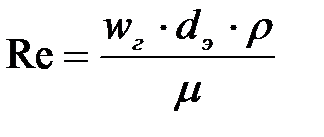 .
.
m - динамическая вязкость газа, Па×с.
Рассмотрим пример решения задачи с использованием оператора цикла WHILE ... DO.
VARdP, L, H, d, w, p, Re, m, wn, wk, hw:real;
BEGIN
H:=1; d:=0.005; p:=1.35; m:=2.45E-6;
writeln(’ wn wk hw’);
readln(wn,wk,hw);
writeln(’ w Re L dP’);
w:=wn;
WHILE w<=wk DO
BEGIN
Re:=w*d*p/m;
IF Re<40 THEN L:=140/Re ELSE L:=16/exp(0.2*ln(Re));
dP:=L*H/d*sqr(w)*p/2;
writeln(w:5:2,’ ’,Re:10,’ ’,L:10,’ ’,dP:10);
w:=w+wh;
END;
END.
Рассмотрим пример решения задачи с использованием оператора цикла REPEAT ... UNTIL.
VARdP, L, H, d, w, p, Re, m, wn, wk, hw:real;
BEGIN
H:=1;
d:=0.005;
p:=1.35;
m:=2.45E-6;
writeln(’ wn wk hw’);
readln(wn,wk,hw);
writeln(’ w Re L dP’);
w:=wn;
REPEAT
Re:=w*d*p/m;
IF Re<40 THEN L:=140/Re ELSE L:=16/exp(0.2*ln(Re));
dP:=L*H/d*sqr(w)*p/2;
writeln(w:5:2,’ ’,Re:10,’ ’,L:10,’ ’,dP:10);
w:=w+wh
UNTIL w>wk
END.
Пример 2.5.3. Составить программу для расчета удельной теплоемкости метана по эмпирической зависимости:
 ,
,
где a, b, c, d, e - эмпирические коэффициенты.
a=4.171;
b=14.45´10-3;
c=0.267´10-6;
d=0.0;
e=-1.722´10-9.
Произвести расчеты для интервала температур от 0 до 500 К, с шагом 50 К.
LABLE1;
CONSTa=4.171;
b=14.45E-03;
c=0.267E-06;
d=0.0;
e=-1.722E-9;
VART, T1, T2, dT, Cp:real;
BEGIN
T1:=0;
T2:=500;
dT:=50;
T:=T1;
writeln(’Т,К Cp, Дж/мольK’);
1: Cp:=a+b*T+c*sqr(T)+d/sqr(T)+e*exp(3*ln(T));
writeln(T:3:0,’ ’,Cp :9:4);
T:=T+dT;
IF T<T2 THEN GOTO 1;
writeln(’Расчет окончен ! ’);
END.
Пример 2.5.4. Составить программу для расчета выражения:
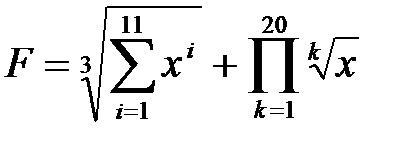 .
.
VARF, S, P, x:real; i, k:integer;
BEGIN
write(’x=’); readln(x);
S:=0;
FOR i:=1 TO 11 DO
S:=S+exp(i*ln(x));
P:=1;
FOR k:=1 TO 20 DO
P:=P*exp(1/k*ln(x));
F:=exp(1/3*ln(S))+P;
writeln(’S=’,S:10,’ P=’,P:10,’ F=’,F:10)
END.
Пример 2.5.5. Составить программу вычисления бесконечного ряда:
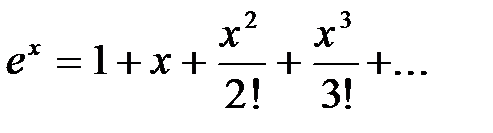 .
.
Условие окончания расчета ряда: 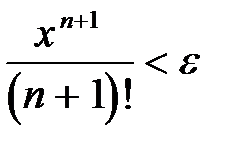 , (e = 0.0001).
, (e = 0.0001).
CONST e=0.0001;
VARi:integer; X, S, Y:real;
BEGIN
write(’Введите значение X =’); readln(X);
i:=0; {Номер слагаемого.}
y:=1; {Значение i-го слагаемого.}
S:=0; {Сумма ряда.}
REPEAT
S:=S+y; {Расчет суммы.}
i:=i+1;
y:=y*x/i {Расчет следующего слагаемого.}
UNTIL y<e;
writeln(’Cумма бесконечного ряда =’, S:10:6);
END.
Пример 2.5.6.
PROGRAM sum;
VAR i,n:integer; s:real;
BEGIN
write('укажите число n ');
readln(n); s:=0; FOR i:=n DOWNTO 1 DO s:=s+i;
writeln('значение суммы ',s);
END.
Таблица 2.5.1
Способы программирования циклов различной структуры
(на примере расчета суммы 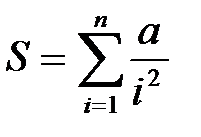 ).
).
| Фрагмент блок – схемы | Операторы |
| 1. Цикл с предварительным условием
| а) С использованием цикла WHILE ... DO. S:=0; i:=1; WHILE i<=n DO BEGIN S:=S+a/sqr(i); i:=i+1 END; б) С использованием операторов IF ... THEN и GOTO. S:=0; i:=1; 1: IF i<=n THEN BEGIN S:=S+a/sqr(i); i:=i+1; GOTO 1 END; |
Продолжение табл. 2.5.1.
| 2. Цикл с последующим условием
| а) С использованием цикла REPEAT ... UNTIL S:=0; i:=1; REPEAT S:=S+a/sqr(i); i:=i+1 UNTIL i>n; б) С использованием операторов IF ... THEN и GOTO. S:=0; i:=1; 1: S:=S+a/sqr(i); i:=i+1 IFi<=n THEN GOTO1; |
Таблица 2.5.2
Расчет сумм (произведений, количества)
| Вид суммы | Фрагмент программы |
1. «Простая» сумма
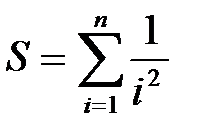
| S:=0; FOR i:=1 TO N DO S:=S+1/sqr(i); |
2. Сумма «с условием»
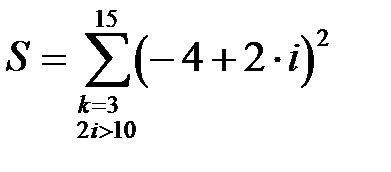
| S:=0; FOR k:=3 TO 15 DO IF 2*i>10 THEN S:=S+sqr(-4+2*i); |
3. Расчет нескольких сумм
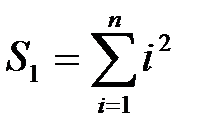 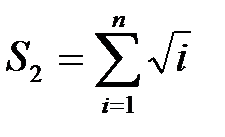
| S1:=0; S2:=0; FORi:=1 TOn DO BEGIN S1:=S1+sqr(i); S2:=S2+sqrt(i) END; |
4. «Сумма в сумме»
а)
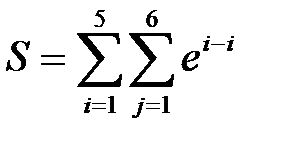
| а) S:=0; FOR i:=1 TO 5 DO FOR j:=1 TO 6 DO S:=S+exp(j-i); |
Продолжение таб. 2.5.2.
б)
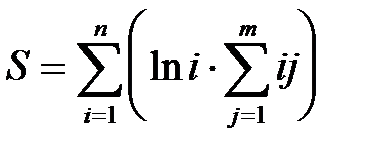
| б) S:=0; FORi:=1 TO n DO BEGIN S2:=0; FORj:=1 TOm DO S2:=S2+i*j; S:=S+ln(i)*S2; END; |
5. Сумма с реккурентной формулой
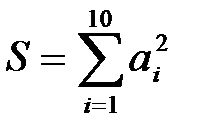 ,
где ai=2*ai-1, a1=1. ,
где ai=2*ai-1, a1=1.
| a:=1; S:=0; FOR i:=1 TO 10 DO BEGIN S:=S+sqr(a); a:=2*a; END; |
Расчет произведения аналогичен расчету суммы, только до цикла пишется оператор P:=1, а в цикле – выражение вида P:=P*<выражение, стоящее под знаком произведения>. Расчет количества – это расчет суммы вида 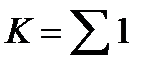 , поэтому до цикла пишется оператор K:=0, а в цикле - K:=K+1. , поэтому до цикла пишется оператор K:=0, а в цикле - K:=K+1.
|
2.6. Одномерные массивы
Массив – это упорядоченный набор фиксированного количества данных одного типа. В Паскале над переменной типа «массив» определено лишь две операции: присваивания и сравнения, поэтому при работе с массивом требуемую операцию следует осуществить над каждым элементом массива.
Основные действия над массивами
1. Формирование массива:
а. Вводом с клавиатуры:
FOR i:=1 TO N DO BEGIN write(’C[’,i,’]=’); readln(C[i]) END;
б. Расчет массива по формуле (например, 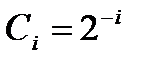 ):
):
FOR i:=1 TO N DO C[i]:=exp(-i*ln(2));
в. Задание массива с помощью функции RANDOM:
randomize; {пишется перед первым употреблением RANDOM}
...
FOR i:=1 TO N DO C[i]:=RANDOM;
2. Вывод массива на экран.
FOR i:=1 TO N DO writeln(’C[’,i,’]=’,C[i]:12);
3. Расчет последовательностей ( 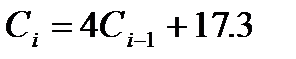 ):
):
C[1]:=3.6; FOR i:=2 TO N DO C[i]:=4*C[i-1]+17.3;
4. Нахождение минимального (или максимального) элемента.
Cmin:=C[1]; FOR i:=2 TO N DO IF C[i]<Cmin THEN Cmin:=C[i];
5. Нахождение номера минимального (или максимального) элемента:
Nmin:=1; FOR i:=2 TO N DO IF C[i]<C[Nmin] THEN Nmin:=i;
6. Нахождение первого (последнего) элемента массива с заданным условием (например, xi<0):
k:=0; REPEAT k:=k+1 UNTIL X[k]<0; (поиск 1-го элемента)
k:=N+1; REPEATk:=k-1 UNTIL X[k]<0; (поиск последнего элемента)
7. Перестановка местами элементов массива с номерами i и j:
r:=C[i]; C[i]:=C[j]; C[j]:=r;
8. Нахождение количества элементов массива, удовлетворяющих условию (например, 2<xi£5):
M:=0; FOR i:=1 TO N DO IF (2<X[i]) AND (X[i]<=5) THEN M:=M+1;
9. Способ задания массива в разделе CONST:
CONST d:ARRAY[1..4] OFreal=(1.2, 3.6, 2e-1, 12.34);
Пример 2.6.1. Составить программу определения минимального элемента массива А(10), суммы элементов, стоящих до него и произведения положительных элементов после него.
VARA:ARRAY[1..10] OF real;
i, MinN:integer;
Min, S, P:real;
BEGIN
{Ввод массива А(10)}
FOR i:=1 TO10 DO
BEGIN
write(’Введите ’,i,’ элемент массива:’); readln(A[i]);
END;
{Поиск номера минимального элемента в массиве А(10)}
Min:=A[1]; MinN:=1;
FOR i:=2 TO 10 DO
IFMin>A[i] THEN
BEGINMin:=A[i]; MinN:=i; END;
writeln(’Минимальный элемент данного массива =’, Min);
{Расчет суммы и произведения}
S:=0; P:=1;
FOR i:=1 TO MinN-1 DOS:=S+A[i];
FOR i:=MinN+1 TO 10 DO
IF A[i]>0 THEN P:=P*A[i];
writeln(’Сумма =’, S:10:6);
writeln(’Произведение =’, P:10:6);
END.
Пример 2.6.2. Найти критерий линейной корреляции по формуле
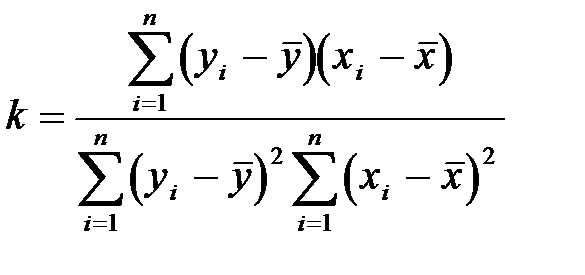
где 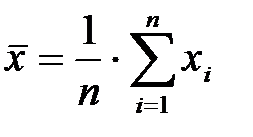 ,
, 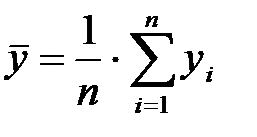 .
.
VAR x, y:ARRAY[1..100] OF real;
Xs, Ys, Sxy, Sx2, Sy2, k:real;
i, n:integer;
BEGIN
{Ввод массивов x и y с клавиатуры.}
write(’Введите количество элементов в массиве. n=’);
readln(n);
FOR i:=1 TO n DO
BEGIN
write(’x’,i, ’=’); readln(x[i]);
write(’y’,i, ’=’); readln(y[i])
END;
{Расчет средних значений массивов x и y}
Xs:=0; Ys:=0;
FOR i:=1 TO n DO
BEGIN
Xs:=Xs+x[i]/n;
Ys:=Ys+y[i]/n
END;
{Расчет коэффициента линейной корреляции}
Sxy:=0; Sx2:=0; Sy2:=0;
FOR i:=1 TO n DO
BEGIN
Sxy:=Sxy+(y[i]-Ys)*(x[i]-Xs);
Sx2:=Sx2+sqr(x[i]-Xs);
Sy2:=Sy2+sqr(y[i]-Ys);
END;
k:=Sxy/(Sy2*Sx2);
{Вывод результата}
writeln(’Коэффициент линейной корреляции. k=’,k:8:6)
END.
Пример 2.6.3. Составить программу случайного задания массива F(20), определения факториала от числа положительных элементов данного массива, а все отрицательные элементы массива заменить их квадратами.
VARF:array [1..20] of real;
i, N:integer;
P:real;
BEGIN
{Задание массива F(20) случайными числами из интервала [-10,10].}
randomize; FOR i:=1 TO 20 DOF[i]:=(1-2*RANDOM)*10;
{Определение количества положительных элементов.}
N:=0;
FOR i:=1 TO 20 DO
IFF[i]>0 THEN N:=N+1;
{Расчет факториала. N!}
P:=1; FOR i:=1 TO N DOP:=P*i;
{Замена отрицательных элементов массива их квадратами.}
FOR i:=1 TO 20 DO
IFF[i]<0 THEN F[i]:= F[i]*F[i];
{Вывод результатов}
writeln(’N!=’,P:10);
FOR i:=1 TO 20 DO writeln(’F’,i,’=’,F[i]:7:4);
END.
Пример 2.6.4. Составить программу для расчета функции по формуле Лагранжа.
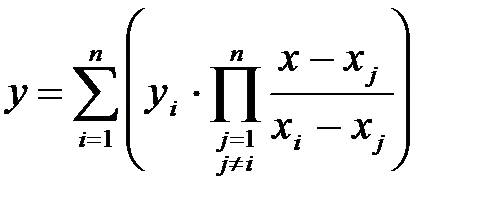
CONST
{Задание значений массивов в программе в виде типизированных констант.}
n=5;
x:ARRAY[1..n] OF real=(1,3,5,7,9);
y:ARRAY[1..n] OF real=(1.33,2.57,3.44,4.74,5.11);
VARx0, S, P:real;
i, j:integer;
BEGIN
{Расчет суммы.}
S:=0;
FOR i:=1 TO n DO
BEGIN
{Расчет произведения.}
P:=1;
FOR j:=1 TO n DO
IF i< >j THEN P:=P*(x0-x[j])/(x[i]-x[j]);
S:=S+y[i]*P
END;
writeln(’f(’,x0:5:2,’)=’,S:12)
END.
Пример 2.6.5. По древней легенде мудрец, придумавший игру шахматы, попросил в награду у султана столько зерен пшеницы, сколько уместиться на шахматной доске, если заполнять ее следующим образом: на первую клетку доски - одно зерно, на вторую - два, на 3-ю - 4, на 4-ю - 8 и т.д. Составить программу для расчета количества зерен.
PROGRAM Chess;
VARi:integer; k, S:real;
BEGIN
k:=1; S:=0;
FOR i:=1 TO 64 DO
BEGIN
S:=S+k;
k:=2*k;
END;
writeln(’S=’,S:12)
END.
Пример 2.6.6.
PROGRAM Xmimax;
VAR x:ARRAY [1..10] of real;
i, n:integer;
xmax, xmin:real;
BEGIN
write('укажите число элементов '); readln(n);
i:=1; xmax:=10.e-37;xmin:=10.e37;
WHILE i<=n DO
BEGIN
write('введи ',i, 'значение
Дата добавления: 2016-06-15; просмотров: 2911;











