АНАЛИЗ ВЗАИМОСВЯЗЕЙ КАЧЕСТВЕННЫХ ПРИЗНАКОВ
Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т. е. состоящим из двух качественно отличных друг от друга значений признака (например, хороший, плохой) (таблица 9.2).
Таблица 9.2 – Таблица для вычисления коэффициентов ассоциации и контингенции.
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+ c+d |
Коэффициенты вычисляются по формулам:
ассоциации: 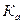 =
= 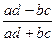 ;
;
контингенции: 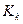 =
= 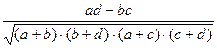 .
.
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если 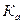 >0,5 или
>0,5 или 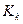 > 0,3.
> 0,3.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова,которые вычисляются по следующим формулам:
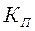 =
= 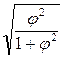 ;
; 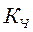 =
= 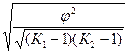 ,
,
где 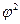 - показатель взаимной сопряженности;
- показатель взаимной сопряженности;
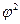 - определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1:
- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки минус 1:
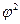 =
= 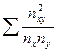 - 1,
- 1,
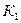 - число значений (групп) первого признака;
- число значений (групп) первого признака;
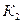 - число значений (групп) второго признака.
- число значений (групп) второго признака.
Чем ближе величины 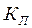 и
и 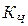 к 1, тем связь теснее.
к 1, тем связь теснее.
Рассмотрим вспомогательную таблицу для расчета коэффициента взаимной сопряженности (таблица 9.3).
Таблица 9.3 – Вспомогательная таблица для расчета коэффициента взаимной сопряженности
y  x x
| I | II | III | Всего |
| I | … | … | 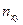
| 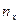
|
| II | … | … | 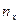
| |
| III | … | … | 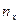
| |
| Итого | 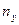
| 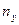
| 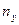
| n |
1+ 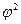 =
= 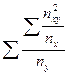 =
= 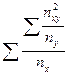 .
.
В статистике существуют модификации коэффициента Пирсона, например через расчет 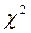 -критерия. Коэффициент взаимной сопряженности(Кп) вычисляется по формуле
-критерия. Коэффициент взаимной сопряженности(Кп) вычисляется по формуле
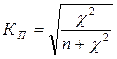 ,
,
 где
где 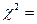
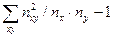 - наиболее распространенный критерий согласия, используемый для проверки статистической гипотезы о виде распределения.
- наиболее распространенный критерий согласия, используемый для проверки статистической гипотезы о виде распределения.
Другой модификацией коэффициента сопряженности Чупрова является
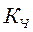 =
= 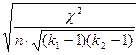 ,
,
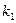 - число строк в таблице;
- число строк в таблице;
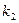 - число граф в таблице;
- число граф в таблице;
n – число наблюдений.
Коэффициент Чупрова изменяется в пределах 0 < Кч < 1.
Дата добавления: 2016-06-18; просмотров: 3941;











