Сложение движений (скоростей)

До сих пор мы рассматривали случаи, когда тело имеет только одно движение по прямой. Но могут быть случаи, когда тело участвует сразу в двух или нескольких движениях. Например, на станции метро 2 человека поднимаются по эскалатору (движущейся лестнице).

Если они стоят, то они участвуют только в одном движении — эскалатора. Если же один из них будет идти вверх по эскалатору, то он будет участвовать сразу в двух движениях, и так как оба эти движения (эскалатора и самого человека по эскалатору) направлены в одну сторону, то движения эти сложатся, и человек поднимется наверх скорее, чем другой человек, оставшийся стоять на эскалаторе. Если же эскалатор будет подниматься, а человек по нему будет идти вниз, то, очевидно, движения будут уже не складываться, а вычитаться одно из другого.

Разберем еще пример. Пароход идет по реке. Здесь мы имеем тоже два движения: движение парохода относительно воды и движение самой воды (течение). Предположим, что скорость первого движения 5 м/сек, а скорость второго 1 м/сек.

Если пароход идет вниз по течению, то оба движения будут иметь одно и то же направление и. следовательно, сложатся; поэтому скорость парохода относительно земли (берега) будет равна сумме скоростей парохода относительно воды и самой воды, т. е. равна 6 м/сек (21,6 км/час).

Если же пароход идет вверх по течению, то его движение направлено в одну сторону, а движение воды—в противоположную; следовательно, скорость парохода относительно берега будет равна разности скоростей парохода (относительно воды) и течения, т. е. 5 м/сек – 1 м/сек = 4 м/сек (14,4 км/час).

Таким образом, мы установили, что сложение движений есть не что иное, как сложение скоростей.

Могут быть случаи, когда тело участвует сразу в трех и больше движениях. Например, пароход идет по реке, а по палубе парохода идет человек. Здесь мы имеем три движения: парохода, воды и человека. Если пароход идет вниз по течению, а человек идет от кормы к носу, то скорость человека относительно берега будет равна сумме скоростей парохода, течения и самого человека. Если пароход идет -вверх по течению, а человек идет по-прежнему от кормы к носу, то скорость человека относительно берега будет равна скорости парохода минус скорость течения и минус скорость самого человека.

Из приведенных примеров нетрудно вывести следующее правило: если тело участвует в нескольких движения у, направления которых или совпадают, или противоположны, то для нахождения скорости тела нужно сложить скорости, направленные в одну сторону, и скорости, направленные в противоположную сторону, и из большей суммы вычесть меньшую, полученная разность и будет равна общей скорости тела, а направление движения тела будет совпадать с направлением скоростей, дающих большую сумму.

Из приведенных примеров мы можем установить также, что скорость всегда имеет определенное направление и, следовательно, скорость, как и сила, есть векторная величина. Графически скорость, подобно силе, также изображается отрезком прямой со стрелкой на конце; отрезок прямой, данный в определенном масштабе, показывает величину скорости, а стрелка — ее направление. Отрезок прямой со стрелкой, изображающей скорость, называется вектором скорости.

Зная это, посмотрим теперь, как складываются скорости, направленные не по одной прямой, а под углом одна к другой.

Пусть через реку переправляется лодка (рис. 27). Предположим, что скорость лодки относительно воды 2 м/сек, а скорость течения реки 1 м/сек. Если бы течения не было, то лодка за 1 секунду продвинулась бы на 2 м в направлении ОА, т. е. скорость лодки равнялась бы вектору α.

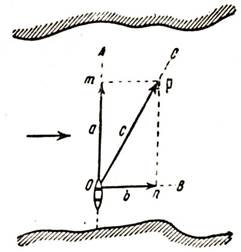
Рис. 27. Сложение скорости лодки со скоростью течения реки (по правилу параллелограмма)

Если бы гребец не греб, то относительно воды лодка не двигалась бы, но относительно берега все же двигалась бы, так как течением ее сносило бы вниз по реке; при этом за 1 секунду лодка продвинулась бы на 1 м в направлении OB, т. е. скорость ее равнялась бы скорости течения—вектору b.

В действительности же лодка участвует сразу в двух движениях, в движении, сообщенном ей гребцом, и в движении воды (течения). Следовательно, через 1 секунду лодка окажется не в точке m и не в точке n, а в точке р.

Таким образом, несмотря на то, что продольная ось лодки будет направлена по линии ОА, двигаться лодка будет в направлении ОС, и скорость лодки относительно берега будет равна вектору с. Отсюда следует, что скорость движения лодки получается как диагональ параллелограмма, построенного на векторах а и b, как на сторонах.

Итак, если тело одновременно участвует в двух движениях, направленных под углом друг к другу, то величина и направление скорости тела определяются диагональю параллелограмма, построенного на скоростях обоих движений, как на сторонах.