Ускорение и скорость в неравномерном движении

Найдем формулу ускорения. Для этого разберем следующую задачу.

Найдем формулу ускорения. Для этого разберем следующую задачу. Самолет оторвался от земли на скорости 72 км/час. Летчик, для того чтобы набрать скорость, выдержал машину над землей, и через 5 секунд после отрыва скорость самолета достигла 126 км/час. Найти ускорение а, предполагая, что в течение указанных 5 секунд самолет двигался прямолинейно и равномерно-ускоренно.

Обозначим скорость в момент отрыва V₀, скорость в конце 5-й секунды после отрыва v_t и переведем км/час в м/сек. Можем написать:

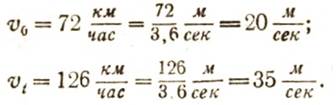
Найдем, насколько увеличилась скорость самолета за 5 секунд. Для этого надо, очевидно, вычесть из скорости v_t скорость v₀:

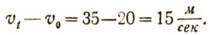
Скорость самолета за 5 секунд увеличилась на 15 м/сек. Так как движение самолета равномерно-ускоренное, то для того, чтобы найти увеличение скорости за 1 секунду, т. е. искомое ускорение α, надо 15 м/сек разделить на 5 секунд: α = 15 м/сек :5 сек.

Но как разделить 15 м/сек на 5 секунд? Если разделить только числовые значения этих величин, то мы получим в частном 3. Очевидно, что это будет неверно, так как ускорение есть механическая величина и не может быть равно отвлеченному числу, а должно иметь свою размерность.

Нечего и говорить, что в частном не может получиться 3 секунды, так как ускорение не может измеряться единицей времени. Но, может быть, в частном получится 3 м/сек ? Нет, и этого не может быть, так как 3 м/сек мы получили бы в том случае, если бы 15 м/сек делили на 5, мы же делим не просто на 5, а на 5 секунд. Какая же величина получится в частном и как ее получить?

Для получения ее следует разделить не только численные величины скорости и времени, но и их размерности, произведя это деление по правилу деления дробей. Для ясности сделаем это деление сначала отдельно:

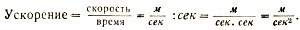
Теперь мы можем написать, чему равно ускорение и в нашем примере:

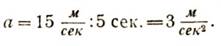
Итак, размерность ускорения есть м/сек².

Теперь вернемся к нашей задаче и составим формулу, пo которой мы эту задачу решили. Мы нашли, что ускорение

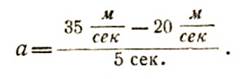
Подставим в это выражение вместо числовых величин принятые нами выше буквенные обозначения. Тогда получим: α = v_t – v₀ : t.

Это и есть формула ускорения. Итак, для того чтобы найти ускорение, надо разность конечной и начальной скоростей разделить на время.

При равномерно-замедленном движении начальная скорость v₀ будет больше конечной скорости v_t, и поэтому ускорение а получится отрицательным.

Теперь найдем формулу для скорости в равномерно ускоренном движении. Для этого разберем следующую задачу. Поезд, выйдя со станции и миновав семафор, достиг скорости 18 км/час; какова будет скорость поезда через 2 минуты, если ускорение α = 0,1 м/сек²?

Решение. Начальная скорость v₀ = 18 км/час. После перевода в м/сек получим, что v₀ = 5 м/сек. Так как ускорение равно 0,1 м/сек² то за 2 минуты, или за 120 секунд, скорость увеличится на 0,1 м/сек² ∙ 120 сек. Если это увеличение скорости за 2 минуты прибавить к начальной скорости (v₀), то, очевидно, мы получим ту скорость, которую поезд имел через 2 минуты после того, как миновал семафор (т. е. конечную скорость v_t):

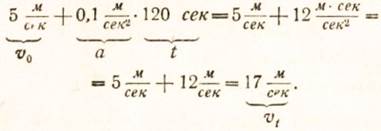
Поменяв местами правую и левую части этого равенства и заменив числовые величины буквенными обозначениями, получим: v_t = v₀ + αt.

Это и есть формула для скорости равномерно-ускоренного движения. Ее можно прочесть так: конечная скорость в равномерно-ускоренном движении равна начальной скорости плюс ускорение, помноженное на время.

В равномерно-замедленном движении, где ускорение отрицательное, формула скорости примет вид: v_t = v₀ - αt.

Теперь вкратце выведем формулу для пути в равномерно-ускоренном движении. Для этого воспользуемся основной формулой равномерного движения: s = vt.

Мы знаем, что в неравномерном движении путь равен средней скорости, помноженной на время. Обозначим среднюю скорость буквой w (дубль-ве). Тогда: s = wt.

Средняя скорость равномерно-ускоренного движения равна полусумме начальной и конечной скоростей (доказательство опускаем;, т. е. средняя скорость = начальная скорость + конечная скорость : 2.

Напишем то же самое в буквенном виде, взяв конечную скорость по формуле равномерно-ускоренного движения:

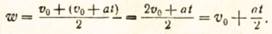
Полученное выражение для средней скорости подставим в формулу для пути (s=wt); после подстановки и умножения получим:

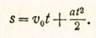
При равномерно-замедленном движении ускорение отрицательное, и формула для пути получится несколько иная:

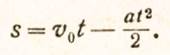
Если в равномерно-ускоренном движении начальная скорость v₀ =0, то формула пути примет вид: s = αt² : 2.

Из предыдущего мы знаем, что t v/α подставив это выражение в последнюю формулу, получим: s = v² : 2α.

Найденные формулы позволяют решать все задачи на равномерно-ускоренное и равномерно-замедленное движения.