Сложение сил. Три случая

При сложении сил могут быть три случая: 1) силы действуют по одной прямой; 2) силы пересекаются друг с другом; 3) силы параллельны друг другу и направлены в одну сторону или же в разные стороны. Отыскивать равнодействующую в этих трех случаях приходится разными способами.

1) Сложение сил, действующих по одной прямой. Если силы А и В направлены в одну сторону (рис. 6, 1), то равнодействующая их R равна их сумме и направленна в туже сторону: R = A+B.

Если силы А и В направлены в противоположные стороны (рис. 6, 2), то равнодействующая их R равна их разности и направлена в сторону большей силы: R = A-B.

Если силы A и В направлены в противоположные стороны и равны друг другу (рис. 6, 2), то равнодействующая их равна нулю: R = A-B = 0.

В этом случае силы, очевидно, уравновешивают друг-друга, и под действием их тело не изменит своего состояния, находится ли оно в состоянии покоя или движения.

Если сил не две, а несколько — А, В, С, D, Е (рис. 6, 4), то для отыскания их равнодействующей надо сложить силы, действующие в одну сторону, и силы, действующие в другую сторону, и из большей суммы вычесть меньшую; равнодействующая R будет направлена в сторону большей суммы: R = A+B – (C+D+E) = A+B-C-D-E.

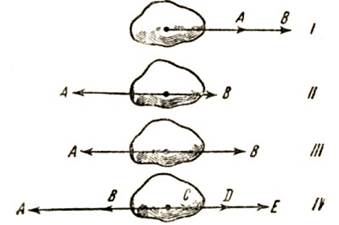
Рис. 6. Сложение сил, действующих по одной прямой

2. Сложение пересекающихся сил. Пусть на тело М действуют две силы Р и Q (рис. 7). Перенесем точки приложения обеих сил по линии их действия в одну точку О. После этого на силах Р и Q построим параллелограмм и проведем диагональ. Эта диагональ и будет по величине и направлению равнодействующей сил P и Q.

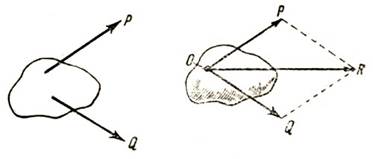
Рис. 7. Сложение двух сил, действующих на тело под углом (правило параллелограмма)

Итак, равнодействующая двух сил Р и Q, действующих на какую-либо точку тела под углом друг к другу, по величине и направлению равна диагонали параллелограмма, построенного на этих силах. Это правило сложения пересекающихся сил называется правилом параллелограмма сил. Сложение сил в этом случае обозначается так:

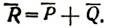
Черточки над величинами показывают, что мы складываем силы не алгебраически, а геометрически, т. е. по правилу параллелограмма.

3. Сложение параллельных сил. а) Силы направлены в одну сторону (рис. 8). Путем несложных геометрических построений (мы их опускаем, чтобы не загружать читателя) нетрудно доказать, что равнодействующая двух параллельных сил в одну сторону, равна их сумме и приложена ближе к большей силе, причем точка приложения равнодействующей делит расстояние между силами на части, обратно пропорциональные силам. Итак:

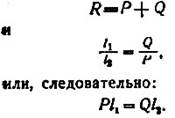
Точка приложения параллельных сил называется центром параллельных сил.

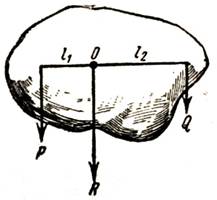
Рис. 8. Сложение двух параллельных сил, направленных в одну сторону

Если на тело действуют не две, а несколько параллельных сил (рис. 9), то для отыскания равнодействующей следует сначала сложить две какие-либо силы, полученную равнодействующую сложить с третьей силой, вновь полученную равнодействующую сложить с четвертой силой и т. д. Последняя полученная равнодействующая и будет равнодействующей всех данных параллельных сил, а точка ее приложения будет центром данных параллельных сил.

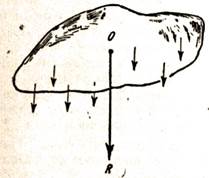
Рис. 9. Сложение нескольких параллельных сил, направленных в одну сторону

б) Силы параллельны, но направлены в разные стороны (рис. 10). Нетрудно доказать (доказательство опускаем), что равнодействующая двух параллельных сил, направленных в разные стороны, равна их разности и направлена в сторону большей силы, причем расстояния от точки приложения равнодействующей до точек приложения сил обратно пропорциональны силам. Итак:

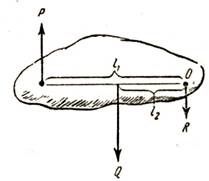
Рис. 10. Сложение двух параллельных сил, направленных в разные стороны

Точка приложения равнодействующей — центр параллельных сил, направленных в разные стороны, — лежит вне этих сил, со стороны большей силы.