Матрицы инциденций и смежности

Графовые модели параллельных алгоритмов в памяти ПВМ обычно представляют в виде двух матричных форм, к которым относятся:
- матрицы инциденций;
- матрицы смежности.

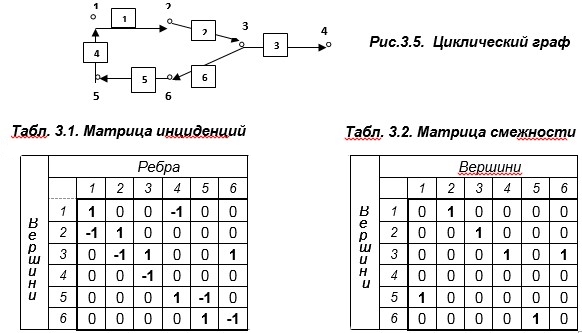
Прямоугольная матрица A [m, n] c элементами a_ij называется матрицей инциденций (табл.3.2) графа параллельного алгоритма, если ее элементы удовлетворяют условиям:

æ +1, если j -е ребро выходит из i -й вершины;

a_ij = í -1, если j -е ребро входит в i -ю вершину;

è 0 - в других случаях.

В каждом столбце матрицы инциденций лишь два элемента отличны от нуля и равны соответственно +1 и -1.

Квадратная матрица В [n, n] c элементами b_ij называется матрицей смежности(табл.3.2) графа параллельного алгоритма, если ее элементы удовлетворяют условиям:
b_ij = 1, если из i -й вершиныв j -ю вершину идет ребро;
b_ij = 0, если из i -й вершиныв j -ю вершину не идет ребро.

Все диагональные элементы матрицы смежностиравны нулю, а остальные ненулевые элементы равны единице.

Пример №3.4. Построим матрицы инциденций (табл.3.1) и смежности (табл.3.2) для помеченного циклического графа, представленного на рис. 3.5.

Пример №3.5. Матрицы инциденций и смежности широко применяются при оценках характеристик параллельных алгоритмов. В частности, для того, чтобы алгоритм с матрицей инциденций А мог быть реализуем в данной вычислительной системе, необходимо и достаточно выполнения условия: - A ^T t ³ t ,

где t = ( t_i, i = 1…n )– вектор временной развертки; t_i – момент включения i–го функционального устройства, выполняющего операцию, находящуюся в i–й вершине графа алгоритма; n – число вершин графа; t = ( t_j, j = 1…m ) - вектор реализации алгоритма; t_j, -время выполнения операции, находящейся в начале j-го ребра; m – число ребер графа.
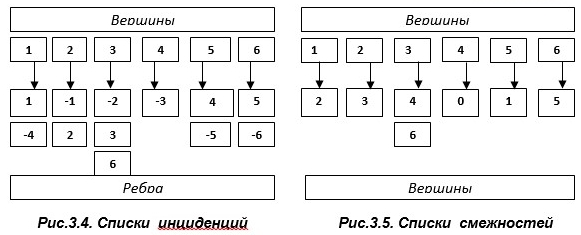
Списочное представление графовых моделей. Как видно из таблиц 3.1 и 3.2, матрицы инциденций и смежности имеют в своем составе большое число нулей. Чтобы не загружать память ПВМ нулевыми элементами, матрицы инциденций и смежности графовых моделей параллельных алгоритмов представляют в виде списков инциденций и смежности. На рис.3.4 и 3.5 приведен возможный вариант списочного представления матриц инциденций и смежности.

Рассмотрим основные типы списков, используемых при создании программного обеспечения вычислительных систем.

Линейный список представляет собой ограниченную последовательность однотипных элементов. Существуют два способа организации линейных списков:
- представление в виде последовательности массивов;
- связное представление с помощью динамических переменных.

В зависимости от организации связи между элементами списка различают:
- односвязные линейные списки;
- двусвязные (линейные и циклические) списки.

При использовании списка как базовой структуры для построения более сложных структур и для экономии памяти ПВМ используется связное сохранение линейных списков с использованием динамических переменных.

В зависимости от организации процедур вставки или удаления элементов существуют следующие типы списков:
- стек – список, в котором занесение и удаление элементов происходит только через один начальный элемент – вершину стека; стек работает по правилу: "последний зашел – первый вышел" ("last in first out") (стек типа "LIFO");
- очередь– список, в котором все вставки вставляются в конец списка, а все удаления происходят с "головы" (начала) списка; очередь выполняется по правилу: "первый зашел – первый вышел" ("first in first out") (стек типа "FIFO").