Лекция 11 ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК. ЧАСТЬ I
11.1 МЕТАЛЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ (Часть II)
11.1.1 Энергия заряженного конденсатора. Объёмная плотность энергии электрического поля
11.2 ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
11.2.1 Классическая теория электропроводности. Определения: сила тока, плотность тока
11.2.2 Закон Ома в дифференциальной форме
11.2.3 Закон Ома для однородного участка цепи. Электрическое сопротивление
11.2.4 Электродвижущая сила. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи
Некоторые примеры
Вопросы для повторения
11.1 МЕТАЛЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ (Часть II)
11.1.1 Энергия заряженного конденсатора.
Объёмная плотность энергии электрического поля
Ранее мы получили – см. (10.8), что для системы, состоящей из N точечных зарядов, WП = 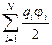 . Учтем, что в конденсаторе на одной обкладке, имеющей потенциал j1, сосредоточен заряд +q =
. Учтем, что в конденсаторе на одной обкладке, имеющей потенциал j1, сосредоточен заряд +q = 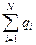 , а на обкладке с потенциалом j2 – заряд -q =
, а на обкладке с потенциалом j2 – заряд -q = 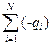 :
:
WП = 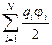 =
= 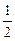 j1
j1 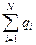 +
+ 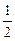 j2
j2 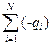 =
= 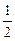 j1q -
j1q - 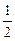 j2q =
j2q = 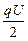 .
.
Таким образом, энергия заряженного конденсатора
WП = 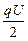 =
= 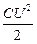 =
= 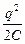 . (11.1)
. (11.1)
Сделаем ещё один шаг: рассмотрим конкретный объект – плоский конденсатор, формулу для расчёта электроёмкости которого и выражение, связывающее E c U, мы получили выше.
WП = 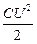 =
= 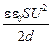 =
= 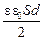
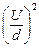 =
= 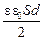 E2.
E2.
Произведение Sd – это объём пространства между обкладками; поделив на него левую и правую части последнего равенства, получим выражение для объёмной плотности энергии (энергии, приходящейся на единицу объёма) электрического поля внутри плоского конденсатора:
wЭЛ = 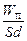 =
= 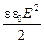 =
= 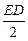 . (11.2)
. (11.2)
На последнем этапе вывода формулы мы использовали полученное ранее выражение для расчёта вектора электрического смещения 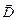 = ee0
= ee0  .
.
Полученное выражение справедливо не только для поля плоского конденсатора, но и для полей, создаваемых другими объектами. Более того, оно позволяет рассчитать объёмную плотность энергии не только электростатического, но и переменного электрического поля, например – распространяющейся в пространстве электромагнитной волны.
11.2 ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ
11.2.1 Классическая теория электропроводности. Определения: сила тока, плотность тока
Электрическим током называется направленное движение зарядов. В металлах – это движение электронов (частиц, имеющих отрицательный заряд), в растворах – ионов (как положительных, так и отрицательных), в газах – и электронов и ионов. Как правило, такое движение возникает под действием внешнего электрического поля (хотя заряды можно перемещать, например, просто механически), при этом если внешнее поле и заряд, перемещаемый им в единицу времени, не меняются, то такой ток называется постоянным.
Силой тока называется выражение вида
I = 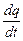 , (11.3)
, (11.3)
где q – перемещаемый заряд, t – время, то есть сила тока – это скорость изменения заряда.
В случае постоянного электрического тока I = const.
В СИ единицей измерения силы тока является ампер, одна из семи основных единиц СИ (о том, что принимается за эталон одного ампера, мы поговорим позднее).
За направление тока выбрано направление движения положительных зарядов, то есть оно определяется направлением вектора напряженности внешнего электрического поля. Сказанное означает, что направление тока всегда противоположно направлению движения электронов и отрицательно заряженных ионов.
 Сама сила тока I является скаляром, то есть ничего не говорит о направлении движения зарядов. Для пространственного описания этого движения вводится вектор плотности тока
Сама сила тока I является скаляром, то есть ничего не говорит о направлении движения зарядов. Для пространственного описания этого движения вводится вектор плотности тока 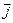 , направление которого совпадает с дрейфовой скоростью
, направление которого совпадает с дрейфовой скоростью 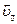 – скоростьюнаправленного, обусловленного воздействием внешнего электрического поля (напряжённостью
– скоростьюнаправленного, обусловленного воздействием внешнего электрического поля (напряжённостью  ) движения положительных зарядов.
) движения положительных зарядов.
Если S – некоторая поверхность (не обязательно плоская), сквозь которую движутся заряды (рис. 11.1), то, по определению плотности тока, должно выполняться соотношение
I = 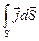 . (11.4)
. (11.4)
Интеграл данного типа нам знаком, он означает, что сила тока является потоком вектора плотности тока через выбранную поверхность S. Если же поверхность – плоская и расположена перпендикулярно вектору 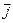 , то она является поперечным сечением проводника, и, обозначив её площадь символом S^, можно записать:
, то она является поперечным сечением проводника, и, обозначив её площадь символом S^, можно записать:
j = 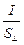 . (11.5)
. (11.5)
Единицей измерения плотности тока является А×м-2.
Согласно классической теории электропроводности, ток в металлах возникает из-за движения электронов. Валентные электроны, оторвавшись от атомов, «обобществляются», в результате чего возникает система из практически неподвижных (испытывающих лишь тепловые колебания) положительно заряженных, регулярно расположенных в пространстве ионов металла и равномерно заполняющего весь объём кристалла отрицательно заряженного электронного газа. Внешнее электрическое поле заставляет двигаться электроны: возникает ток.
На примере хорошего проводника – меди – оценим концентрацию электронов в металле (их число в единице объёма). Нам известно, что в одном моле любого вещества содержится NA (число Авогадро, NA » 6,02×1023) структурных элементов (атомов, молекул), причём 1 моль меди имеет массу mCu = 0,064 кг. В одном кубическом метре Cu содержится n атомов; согласно справочным данным, масса 1 м3 меди (то есть её плотность) равна 8,9×103 кг. Составив пропорцию, получаем, что
n = NA 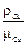 = 6,02×1023×
= 6,02×1023× 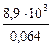 » 8×1028 (м-3).
» 8×1028 (м-3).
Будем считать, что каждый атом меди явился «поставщиком» в электронный газ одного электрона, тогда n » 8×1028 м-3 – это и концентрация электронов в кристалле. Для сравнения отметим, что при нормальных атмосферных условиях концентрация молекул в воздухе почти в 3000 раз меньше!
Подобно молекулам идеального газа, электроны находятся в постоянном тепловом движении. Скорость такого движения весьма высока и при комнатной температуре среднеквадратичная скорость этого движения составляет
uКВ = 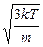 =
= 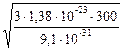 » 1,1×105 (м/с),
» 1,1×105 (м/с),
то есть в 14 раз выше первой космической скорости для Земли (в данной формуле k – постоянная Больцмана, T - термодинамическая температура, m – масса электрона). Однако эта скорость характеризует хаотическое движение электронов, а для протекания тока важна скорость их направленного движения (дрейфовая). У электронов в меди, например, в обычных условиях uД составляет величину порядка 10-3 м/с, то есть
uД << uКВ.
11.2.2 Закон Ома в дифференциальной форме
Во внешнем электрическом поле напряжённостью E на электрон (заряд e, масса m) в металле действует сила F = eE. Используя формулу второго закона Ньютона, для ускорения, приобретаемого электроном, запишем:
a = 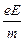 . (11.6)
. (11.6)
При равноускоренном движении за время t скорость электрона достигает величины uД = at, причём она росла бы и дальше, но, согласно классической теории, электроны, как атомы идеального газа, постоянно сталкиваются с ионами металла, теряют скорость и меняют её направление (а для тока важна скорость именно направленного движения), поэтому вынуждены разгоняться вновь и вновь. Если обозначить среднюю длину свободного пробега электронов от одного столкновения до другого буквой l, то время t, соответствующее такому пробегу, можно выразить, как
t = 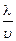 »
» 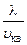 =
= 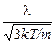 . (11.7)
. (11.7)
Здесь учтено, что полная скорость u движения электронов в каждый момент времени складывается из дрейфовой и тепловой, причём uД << uКВ, поэтому u » uКВ.
Таким образом, достижимое значение дрейфовой скорости составляет
uД = at = 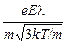 =
= 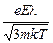 . (11.8)
. (11.8)
Теперь получим выражение, связывающее дрейфовую скорость с плотностью тока j.
 Пусть по участку цилиндрического проводника, имеющему длину l и площадь поперечного сечения S, идёт ток I. Представим себе, что в этом участке изначально находилось N свободных электронов, которые под действием электрического поля движутся со скоростью uД вдоль проводника (в направлении, обратном направлению вектора
Пусть по участку цилиндрического проводника, имеющему длину l и площадь поперечного сечения S, идёт ток I. Представим себе, что в этом участке изначально находилось N свободных электронов, которые под действием электрического поля движутся со скоростью uД вдоль проводника (в направлении, обратном направлению вектора 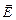 ). Электроны, находившиеся ближе к правому «дну» цилиндрического участка (рис. 11.2), покинут данный участок проводника раньше, остальные – позже. Последними покинут данный участок электроны, находившиеся в начальный момент времени у левого «дна», то есть общее время, которое потребуется для того, чтобы весь заряд, равный eN, прошёл через данный участок, составляет t0 = l/uД. При этом сила тока может быть представлена, как
). Электроны, находившиеся ближе к правому «дну» цилиндрического участка (рис. 11.2), покинут данный участок проводника раньше, остальные – позже. Последними покинут данный участок электроны, находившиеся в начальный момент времени у левого «дна», то есть общее время, которое потребуется для того, чтобы весь заряд, равный eN, прошёл через данный участок, составляет t0 = l/uД. При этом сила тока может быть представлена, как
I = 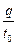 =
= 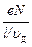 =
= 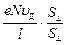 =
= 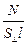 euДS^ = enuДS^,
euДS^ = enuДS^,
и плотность тока j оказывается связанной с концентрацией n свободных носителей заряда (электронов) и с их дрейфовой скоростью соотношением
j = 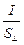 = enuД. (11.9)
= enuД. (11.9)
Если заряд переносится носителями обоих знаков (ионами в растворах и в газах, электронами и дырками в полупроводниках и т. д.), то в итоговом выражении для плотности тока следует учесть вклад и тех и других:
j = |q1|n1uД1 + |q2|n2uД2. (11.10)
Вернувшись к формуле 11.8, выражение 11.9 для плотности тока в металле перепишем в виде
j = en 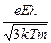 =
= 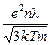 E. (11.11)
E. (11.11)
Множитель, стоящий перед напряжённостью электрического поля E, принято обозначать буквой s; он называется удельной электропроводностью. Очевидно, его величина определяется свойствами проводника (концентрацией в нём носителей заряда, их длиной свободного пробега l); s зависит также от температуры. В итоге, с учётом того, что в нашем случае вектор 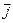 направлен туда же, куда и вектор
направлен туда же, куда и вектор 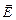 , мы получаем формулу, которая выражает закон Ома в дифференциальной форме:
, мы получаем формулу, которая выражает закон Ома в дифференциальной форме:
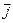 = s
= s 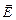 . (11.12)
. (11.12)
11.2.3 Закон Ома для однородного участка цепи. Электрическое сопротивление
Учтём теперь, что в ситуации, изображённой на рис. 11.2, сила тока I = jS^, а также то, что в однородном электрическом поле внутри проводника вдоль силовой линии
E = -dj/dl = (j1 - j2)/l = U/l.
Исходя из сказанного, нетрудно получить, что I = 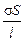 U. Нам осталось ввести обозначение
U. Нам осталось ввести обозначение 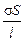 =
= 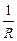 , чтобы получить формулу, известную, как закон Ома для однородного участка цепи:
, чтобы получить формулу, известную, как закон Ома для однородного участка цепи:
I = 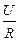 . (11.13)
. (11.13)

Согласно этому закону, сила тока I на однородном участке цепи (не содержащем источников э. д. с.)прямо пропорциональна разности потенциаловU на концах этого участка и обратно пропорциональна электрическому сопротивлению R этого участка– рис. 11.3.а). Элемент цепи, обладающий лишь электрическим сопротивлением, называется резистором и на схемах изображается в таком масштабе, как это представлено на рис. 11.3.б). На этом же рисунке показано, как на схемах изображается электрический конденсатор (рис. 11.3.в).
Таким образом, электрическое сопротивление по определению вводится, как коэффициент пропорциональности между силой тока и разностью потенциалов:
R = 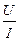 . (11.14)
. (11.14)
Но R = 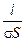 , и, вводя обозначение r =
, и, вводя обозначение r = 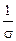 (данный коэффициент носит название удельного сопротивления), запишем:
(данный коэффициент носит название удельного сопротивления), запишем:
R = r 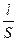 . (11.15)
. (11.15)
Полученная формула позволяет сделать вывод о том, что электрическое сопротивление зависит от материала (М) проводника – то есть от удельного сопротивления r, от его размера (Р) – то есть от l и S, и от его формы (Ф): в частности, выражение (11.15) получено нами для проводника-цилиндра, рис. 11.2.
Электрическое сопротивление измеряется в омах, 1 Ом = 1 В×А-1.
В заключение данного параграфа заметим, что из формул 11.11 – 11.15 следует, что удельное сопротивление металла должно зависеть от температуры, будучи пропорциональным 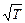 :
:
r = 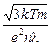 . (11.16)
. (11.16)
На деле это не так, но то, с чем может быть связано расхождение между выводами теории и данными эксперимента, мы обсудим позднее.
11.2.4 Электродвижущая сила. Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи
Если бы электрический ток создавался только теми электронами, которые оторвались от атомов кристаллической решётки проводника, то спустя некоторое время они должны были бы покинуть металл, а ток – закончиться. Для существования постоянного тока необходимо непрерывно восполнять их число, для чего требуется выполнять работу против сил электрического поля, которые стремятся выровнять потенциальную энергию системы. Разделять заряды, поддерживая разность потенциалов на концах проводника, могут силы неэлектрической природы, связанные с механическими, химическими явлениями, фотоэффектом и т.д. Силы, осуществляющие перемещение электрических зарядов против сил электростатического поля, называются сторонними. Работа AСТтаких сил тем больше, чем больше перенесённый заряд q. Отношение работы сторонних сил по перенесению заряда к величине этого заряда называется электродвижущей силой (э. д. с.) и обозначается буквой E:
E = 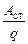 . (11.17)
. (11.17)
В СИ э. д. с., как и потенциал, измеряется в вольтах.
 Устройство, осуществляющее разделение зарядов, называется источником э. д. с., примерами таких источников могут служить электрофорные машины, разделяющие заряд с помощью сил трения, химические батареи и аккумуляторы, работа которых связана с протеканием внутри них химических реакций, солнечные батареи (разделять заряд в них помогает свет).
Устройство, осуществляющее разделение зарядов, называется источником э. д. с., примерами таких источников могут служить электрофорные машины, разделяющие заряд с помощью сил трения, химические батареи и аккумуляторы, работа которых связана с протеканием внутри них химических реакций, солнечные батареи (разделять заряд в них помогает свет).
На рис. 11.4 показано, как на электрической схеме принято изображать химический источник э. д. с. (длинная черта означает положительный электрод, короткая – отрицательный). Существенно, что такой источник обладает внутренним сопротивлением r, которое зависит от материала (М) электролита и его температуры, размеров (Р), формы (Ф) и взаимного расположения элементов конструкции устройства. Химические реакции, приводящие к разложению электролита на ионы внутри источника, в течение достаточно долгого времени могут поддерживать положительный потенциал на одном из электродов и отрицательный – на другом, обеспечивая, тем самым постоянство электрического тока в цепи.
 Участок цепи, содержащий источник э. д. с., называется неоднородным; пример такого участка изображён на рис. 11.5. Предполагается, что к клеммам 1 и 2 подключены другие элементы цепи (на рисунке они не изображены), что обеспечивает прохождение на участке 1-2 постоянного электрического тока (на рисунке – от точки 1 к точке 2).
Участок цепи, содержащий источник э. д. с., называется неоднородным; пример такого участка изображён на рис. 11.5. Предполагается, что к клеммам 1 и 2 подключены другие элементы цепи (на рисунке они не изображены), что обеспечивает прохождение на участке 1-2 постоянного электрического тока (на рисунке – от точки 1 к точке 2).
На каждый движущийся заряд на данном участке цепи действуют силы электрического поля; их работа AЭ = q(j1 - j2), поскольку на рисунке ток идёт от точки с потенциалом j1 к точке с потенциалом j2. Кроме этого на участке действуют сторонние силы, совершающие свою работу AСТ = Eq. Источник включён так, что сторонние силы на данном участке сонаправлены с электрическими; общая работа A = AЭ + AСТ = q(j1 - j2) + Eq. Если бы батарея была включена «наоборот», общая работа рассчитывалась бы, как A = q(j1 - j2) - Eq, и это даёт возможность записать:
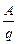 =
= 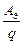 ±
± 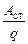 = j1 - j2 ± E.
= j1 - j2 ± E.
Ранее, в отсутствие источников э. д. с., разность потенциалов j1 - j2 мы обозначали символом U, теперь
U = j1 - j2 ± E (11.18)
и это уже не разность потенциалов, а падение напряжения на участке 1-2. Принимая во внимание, что общее сопротивление RОБЩданного участка складывается из сопротивлений последовательно соединённых батареи (r)и резистора (R), то есть RОБЩ = R + r, можно записать закон Ома для неоднородного (содержащего источник э. д. с.) участка цепи:
 I =
I = 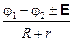 . (11.19)
. (11.19)
В этой формуле j1 – потенциал той точки, откуда идёт ток, а j2 – точки, куда он идёт; «плюс» или «минус» перед E выбирается с учётом того, помогает ли источник силам электрического поля (+), или мешает (-).
Для замкнутой (полной) цепи – рис. 11.6 – точки 1 и 2 фактически совпадают, j1 = j2, то есть можно записать:
I = 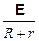 . (11.20)
. (11.20)
Мы получили известную из школьной программы физики формулу закона Ома для замкнутой цепи.
Некоторые примеры
- В обычных электробытовых приборах сила тока, как правило, не превышает 1 А – 2 А. В сварочном аппарате сила тока может составлять 20 А – 1000 А. Сверхпроводящие обмотки электромагнитов Большого адрононного коллайдера рассчитаны на токи выше 104 А. При магнитных бурях в верхних слоях приполярных областей атмосферы Земли возникают токи силой более 105 А.
- Для человека смертельной считается сила тока 100 мА. При казни на электрическим стуле через человека пропускают ток до 6 А.
- Решая задачи о зарядке аккумуляторов, следует помнить, что при зарядке совершается работа против сторонних сил, поэтому, применяя формулу закона Ома для неоднородного участка цепи, перед значком э. д. с. следует писать знак «минус».
- Важной характеристикой аккумулятора является его ёмкость, которая совсем не то же самое, что электроёмкость конденсатора: она измеряется в ампер-часах и даёт информацию о накопленном данным устройством заряде и времени, в течение которого этот заряд может быть израсходован.
- В вагонах поезда используются щелочные и кислотные аккумуляторные батареи. Э. д. с. кислотного аккумулятора равна 2,1 В – 2,15 В, щелочного – около1,45 В (в настоящее время в пассажирских вагонах используются в основном щелочные аккумуляторы).
Вопросы для повторения
1. Сравните формулы для расчёта энергии заряженного конденсатора и заряженного уединённого проводника. Какие из этих формул имеют одинаковый вид?
2. Выведите формулу для расчёта плотности энергии электрического поля.
3. Что называется силой тока, плотностью тока, дрейфовой скоростью носителей заряда?
4. На данной лекции говорилось о четырёх вариантах закона Ома. Перечислите соответствующие варианты.
5. Из формулы закона Ома для неоднородного участка цепи получите формулу закона Ома для замкнутой цепи.
6. Что называется электродвижущей силой? В каких единицах она измеряется в СИ?
7. Какие силы называются сторонними? Приведите примеры.
8. Что называется падением напряжения на участке цепи? В каком случае падение напряжения и разность потенциалов на участке цепи совпадают?
9. Что называется электрическим сопротивлением? В каких единицах оно измеряется в СИ? От чего зависит электрическое сопротивление.
Дата добавления: 2020-02-05; просмотров: 615;











