Лекция 9 ЭЛЕКТРОСТАТИКА. ЧАСТЬ III

9.1 ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

9.1.1 Примеры применения теоремы Гаусса для электрического поля в вакууме (продолжение)

9.1.2 Электрический диполь. Диполь в однородном и неоднородном электрических полях

9.2 ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

9.2.1 Поведение молекул диэлектрика в электрическом поле

9.2.2 О пьезоэффекте и сегнетоэлектричестве

Некоторые примеры

Вопросы для повторения

9.1 ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСОКОГО ПОЛЯ

9.1.1 Примеры применения теоремы Гаусса для электрического поля в вакууме (продолжение)

б) Поле равномерно заряженной бесконечно длинной тонкой прямой нити

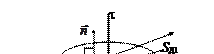Пользуясь теоремой Гаусса, выведем формулу для напряжённости электрического поля, создаваемого длинной прямой тонкой нитью с линейной плотностью заряда t (зарядом dQ, приходящимся на единицу длины dl, t = ) на некотором расстоянии r от этой нити.

Действуем по алгоритму, изложенному на предыдущей лекции: рисуем чертёж, изображаем силовые линии, выбираем точку М, находящуюся на расстоянии r от нити, проводим через неё одну из силовых линий, после чего выбираем замкнутую поверхность, соответствующую симметрии задачи и проходящую через эту точку. Очевидно, такой поверхностью будет цилиндр, ось которого совпадает с нитью (рис. 9.1, предполагается, что нить заряжена положительно).

Следующий шаг – вычисление потока вектора через всю поверхность цилиндра как сумму интегралов по двум донышкам цилиндра S_Д1 и S_Д2, а также по его боковой поверхности S_Б. В вычислениях учитываем, что нормали к донышкам перпендикулярны силовым линиям, а нормали в любой точке боковой поверхности (например, – в точке M) направлены вдоль силовых линий, проходящих через эти точки.

F_E = = + + =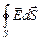

= + + = .

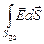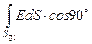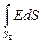Принимая во внимание то, что в силу симметрии цилиндра напряжённость электрического поля в любой точке его боковой поверхности одинакова, а также то, что площадь боковой поверхности цилиндра, имеющего высоту h, равна 2prh, запишем:

F_E = 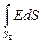= E = 2prhE.

Заряд, находящийся в области, ограниченной поверхностью цилиндра, сосредоточен на участке нити длиной h и равен th.Согласно теореме Гаусса F_E = th/e₀, или

2prhE = .

Сократив h в обеих частях равенства, получаем формулу для расчёта напряжённости электрического поля тонкой прямой заряженной нити:

E = 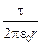. (9.1)

в) Поле равномерно заряженной плоскости

Получим формулу для расчёта напряжённости электрического поля, создаваемого равномерно заряженной плоскостью с поверхностной плотностью заряда s (зарядом dQ, приходящимся на единицу площади dS, то есть s = ).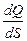

Точно так же, как это мы делали ранее, создаём чертёж, изображаем силовые линии, выбираем точку М, находящуюся на некотором расстоянии плоскости, проводим через неё одну из силовых линий, после чего выбираем замкнутую поверхность, соответствующую симметрии задачи и проходящую через эту точку. В данном случае в качестве такой поверхности можно также выбрать цилиндр, ось которого проходит через выбранную точку M и перпендикулярна заряженной плоскости (на рис. 9.2. её заряд принят положительным).

Теперь вычислим поток вектора через всю поверхность цилиндра как сумму интегралов по двум донышкам цилиндра S_Д1 и S_Д2, а также по его боковой поверхности S_Б. В Вычислениях учитываем, что нормали к донышкам параллельны силовым линиям, а нормали в любой точке боковой поверхности направлены перпендикулярно силовым линиям, проходящих через эти точки.

F_E = = + + =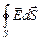

= + + = + .

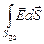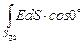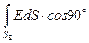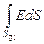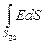В силу симметрии значения напряжённости в любых точках донышек одинаковы, площади донышек равны, следовательно,

F_E = ES_Д1 + ES_Д2 = 2ES₀.

Заряд, охватываемый цилиндром, сосредоточен на участке поверхности площадью S₀ и равен sS₀. Применив теорему Гаусса, получим: F_E = 2ES₀ = , или в вакууме напряжённость электрического поля равномерно заряженной плоскости на любом расстоянии от этой плоскости

E = . (9.2)

г) Поле двух равномерно заряженных плоскостей с зарядами, равными по величине, но имеющими противоположные знаки

Для вычисления напряжённости воспользуемся только что полученной формулой (9.2), и принципом суперпозиции. На рис. 9.3 представлен вид сбоку такой системы; силовые линии положительно заряженной плоскости (поверхностная плотность заряда +s) изображённая сплошными, отрицательно заряженной (поверхностная плотность заряда -s) – пунктирными линиями.

Поскольку для обеих плоскостей E не зависит от расстояния и одинаково по модулю, то в областях I и III соответствующие вектора напряжённости в сумме дают ноль, зато в области II результирующая напряжённость E_РЕЗ = 2E, то есть

E = . (9.3)

Итак, электрического поля вне данной системы нет, оно как бы «конденсируется» в пространстве между двумя плоскостями, поэтому такую систему называют плоским конденсатором, а заряженные плоскости – обкладками этого конденсатора. Заметим: формула (9.3) получена в предположении, что обкладки-плоскости безграничны.

9.1.2 Электрический диполь. Диполь в однородном и неоднородном электрических полях

Сравнивая закон Кулона с законом Всемирного тяготения, на первый взгляд создаётся впечатление, что, точно так же, как и гравитационное воздействие, электрические поля от различных объектов должны ощущаться на громадных, вплоть до границ Вселенной, расстояниях. На деле это, однако, не совсем так. Дело в том, что в целом окружающий нас мир не обладает избыточным электрическим зарядом, и воздействие близко расположенных зарядов разных знаков на больших расстояниях практически компенсируются. Примером объекта, на котором это можно достаточно легко продемонстрировать, является электрический диполь: система из одинаковых по величине, но имеющих противоположные знаки зарядов +q и -q, расположенных малой (по сравнению с расстоянием r до точки наблюдения) дистанции l друг от друга. «Связь» между зарядами может быть как абсолютно жёсткой (l = const), так и упругой (возможно небольшое изменение l под действием внешних сил).

Для количественного описания свойств диполя вводится дипольный электрический момент: вектор , определяемый, как

= q , (9.4)

где – вектор, по длине равный расстоянию между зарядами диполя и направленный от отрицательного заряда к положительному (см. рис. 9.4.а). На рис. 9.4.б) и 9.4.в) приведены другие примеры графического изображения электрических диполей.

Понятно, что на большом расстоянии r от диполя (см. рис. 9.5) притяжение заряда одного знака практически уравновешивается отталкиванием от заряда противоположного знака. Можно показать, что при r >> l напряжённость электрического поля, создаваемого диполем, обратно пропорциональна уже не квадрату, а кубу расстояния (и при этом зависит от угла q, под которым ведётся наблюдение):

E =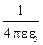 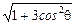. (9.5)

Реально силы кулоновского электростатического взаимодействия обычно учитываются на расстояниях, не превышающих десятка километров. В то же время на очень малых (меньших, чем диаметр атомного ядра, то есть менее 10^-15 м) кулоновскими силами зачастую также можно пренебречь, так как на таких расстояниях существенным становится сильное взаимодействие между элементарными частицами.

Электрический диполь может служить моделью молекул, из которых состоят многие окружающие нас вещества, и поэтому важное практическое значение имеет рассмотрение того, как такой объект ведёт себя в электрическом поле.

а) В однородном поле (вектор везде одинаков по величине и направлению, силовые линии являются параллельными и расположенными на равном расстоянии друг от друга прямыми) на положительный и отрицательный полюса диполя действуют одинаковые по величине, но противоположные по направлению силы (рис. 9.6).

На положительный полюс действует сила, по определению направленная туда же, что и вектор (на рисунке - направо), на отрицательный полюс – в противоположную сторону (на рисунке – налево). Под действием возникающего момента пары сил происходит разворот диполя таким образом, чтобы вектор оказался направлен туда же, куда и вектор . В дальнейшем силы, действующие на полюса, будут стремиться «растянуть» диполь, но ни повернуть, ни заставить его двигаться они уже не смогут, так как эти силы равны по величине, противоположны по направлению и при этом лежат на одной прямой.

б) Если поле неоднородно (в одной части рисунка силовые линии расположены гуще, чем в другой), то диполь не только поворачивается, но одновременно начинает втягиваться в область сильного поля. Действительно, силы теперь, во-первых, направлены в разные стороны, причём под углом, не равным 180º, друг к другу (они по-прежнему являются касательными к силовым линиям), и, во-вторых, неодинаковы по величине, поскольку в области сгущения силовых линий напряжённость электрического поля выше: рис. 9.7.

9.2 ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

9.2.1 Поведение молекул диэлектрика в электрическом поле

Согласно классической теории электропроводности, главной особенностью диэлектриков, отличающей их от проводников, является отсутствие в них свободных зарядов, способных перемещаться под действием электрического поля. В связи с этим все диэлектрики по электрическим свойствам молекул и атомов, из которых они состоят, можно условно разделить на две основные группы: на полярные и неполярные.

В полярных диэлектриках атомы в молекулах располагаются таким образом, что саму молекулу можно считать электрическим диполем, поскольку у неё есть два полюса, заряженные положительно и отрицательно. Типичными примерами полярных диэлектриков являются H₂O, NH₃, HCl. Молекулы таких веществ обладают электрическим дипольным моментом , величина которого зависит от формы молекул, размеров и взаимного расположения атомов, из которых они состоят.

Атомы в молекулах неполярных диэлектриков расположены таким образом, что геометрические центры областей сосредоточения положительных и отрицательных зарядов совпадают, и поэтому электрический дипольный момент молекулы оказывается равным нулю. Примеры таких веществ: H₂, N₂, CCl₄

Введём вектор 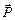, который называется поляризованностью вещества; его величина равна отношению суммарного электрического дипольного момента некоторого объёма DV диэлектрика к величине этого объёма (единица измерения 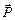в СИ – Кл×м^-2).

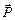= . (9.6)

Понятно, что в обычных условиях поляризованность неполярных диэлектриков равна нулю (в них все = 0). Но в отсутствие внешних воздействий поляризованности нет и у полярных диэлектриков: поскольку ориентация их молекул носит хаотический характер, то для любого элемента объёма = 0.

Однако, при внесении диэлектриков в электрическое поле картина меняется. Элементарные диполи – молекулы полярных диэлектриков – в электрическом поле разворачиваются. Взаимодействие молекул друг с другом, играет роль сил трения, поэтому все молекулы сразу развернуться по полю не могут. 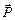Свой вклад в нарушение порядка дают и тепловые колебания, тем не менее, в области не слишком сильных полей можно считать, что возникающий суммарный дипольный момент единицы объёма прямо пропорционален величине внешнего электрического поля, то есть ~ , и, следовательно, ~ (рис. 9.8.а).

Под действием внешнего электрического поля молекулы неполярного диэлектрика повернуться не могут, однако они начинают деформироваться, «растягиваться», то есть сами становятся диполями (рис. 9.8.б). Чем больше , тем сильнее растяжение и, соответственно, дипольный момент каждой единицы объёма. Таким образом, и для неполярного диэлектрика ~ , или ~ .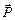

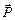Сама сумма дипольных моментов пропорциональна числу молекул ( ~ N), следовательно, с учетом того, что = n, где n – концентрация молекул, ~ n .

Последнее выражение можно записать в виде равенства, введя в него в виде сомножителей электрическую постоянную e₀ и некоторый параметр a, определяемый свойствами диэлектрика (характером отдельных связей между атомами в молекулах, температурой и т. д.):

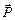= e₀an . (9.7)

Произведение k = an называется диэлектрической восприимчивостью вещества, это безразмерная величина.

Таким образом, для не слишком сильных полей выполняется соотношение, полученное впервые П.Дебаем

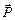= e₀k . (9.8)

9.2.2 О пьезоэффекте и сегнетоэлектричестве

У подавляющего большинства веществ, не проводящих электрический ток, диэлектрическая восприимчивость k не слишком велика и является постоянной величиной. Однако, нужно помнить, что она отражает свойства молекул вещества откликаться на воздействие внешнего электрического поля и поэтому может зависеть от величины (в случае электростатического поля), а также от его частоты и амплитуды (в случае переменного поля).

К поляризации диэлектрика могут привести и другие внешние воздействия, например, – механическое сжатие или растяжение (явление электрострикции и пьезоэффект), его нагрев (пироэлектрический эффект). Пример, иллюстрирующий влияние растяжения на фрагмент кристаллической решётки, представлен на рис. 9.9: если в обычном состоянии центры систем положительных отрицательных зарядов совпадали, и электрический дипольный момент системы был равен нулю, то деформация приводит к смещению атомов и появлению у данного фрагмента некоторого , тем большего, чем сильнее деформация. Возможен и обратный пьезоэффект, при котором под действием электрического поля происходит механическая деформация образца (например, – кристалла кварца). Явление находит применение в устройствах, преобразующих механическое воздействие в электрический сигнал, например, – в микрофонах, датчиках, используемых при испытаниях на прочность деталей различных машин. Преобразование электрического сигнала в механическую деформацию позволяет создавать, например, миниатюрные наушники для плееров.

Между соседними молекулами диэлектрика может существовать настолько сильное взаимодействие, что все электрические диполи в пределах области, объединяющей сотни тысяч молекул, оказываются ориентированными в одном направлении. Такие области называются доменами; кривая зависимости у таких веществ имеет вид петли. Данные материалы (сегнетова соль KNaC₄H₄O₆·4H₂O, титанат бария BaTiO₃ и др.) называются сегнетоэлектриками (или ферроэлектриками), их поведение в электрическом поле во многом аналогично поведению в магнитном поле ферромагнетиков, о которых мы будем говорить позднее в разделе «Магнитные свойства вещества».

Некоторые примеры

- Электрический дипольный момент молекулы HCl равен 3,5×10^-30 Кл×м; у молекулы воды p_e = 6,2×10^-30 Кл×м.

- Кварцевая пластина толщиной 1 мм под действием напряжения 100 В изменяет свою толщину на 2,3×10^-7 мм.

Вопросы для повторения

1. Сформулируйте теорему Гаусса для электрического поля в вакууме; запишите соответствующую формулу и поясните смысл входящих в формулу величин.

2. Продемонстрируйте, как применяется теорема Гаусса для вычисления напряженности электрического поля, создаваемого прямой, тонкой, бесконечной, равномерно заряженной нитью.

3. Продемонстрируйте, как применяется теорема Гаусса для вычисления напряженности электрического поля, создаваемого равномерно заряженной плоскостью.

4. Выведите формулу для вычисления напряженности электрического поля, создаваемого двумя параллельными равномерно и при этом разноимённо заряженными плоскостями.

5. Что называется полярными и неполярными диэлектриками? Как молекулы этих диэлектриков ведут себя в электрическом поле?

6. Что называется поляризованностью вещества? В каких единицах поляризованность измеряется в СИ?

7. Какова связь поляризованности диэлектрика с напряжённостью внешнего электрического поля?