Лекция 8 ЭЛЕКТРОСТАТИКА. ЧАСТЬ II
8.1 ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
8.1.1 Работа по переносу заряда в электрическом поле
8.1.2 Потенциал – энергетическая характеристика электрического поля. Графическое отображение потенциала (эквипотенциальные линии)
8.1.3 Связь потенциала и напряжённости электрического поля
8.1.4 Теорема Гаусса для электрического поля в вакууме
8.1.5 Примеры применения теоремы Гаусса для электрического поля в вакууме
Некоторые примеры
Вопросы для повторения
8.1 ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСОКОГО ПОЛЯ
8.1.1 Работа по переносу заряда в электрическом поле
Решая задачи механики, мы убедились в том, что использование понятий «работа» и «энергия» позволяет получать ответы даже в тех случаях, когда в ходе перемещения тела силы, действующие на него, менялись по величине. Подобная проблема особенно актуальна в неоднородном электрическом поле, ведь даже сила взаимодействия двух точечных зарядов существенным образом зависит от расстояния между ними.
Для описания изменения энергии заряженных тел в электрическом поле вводится энергетическая характеристика этого поля, которая называется потенциалом.
Об электрическом поле мы говорим, поскольку в каждой точке пространства на заряд, помещаемый в это поле, действует определённая сила (Кулона). Силы электростатического поля являются консервативными (их работа не зависит от формы траектории, по которой перемещается тело, а определяется лишь его начальным и конечным положениями). Работа сил такого поля равна убыли потенциальной энергии тела.
Рассчитаем работу, которую совершают силы электрического поля перемещая один точечный заряд q, находившийся изначально на расстоянии r1 от второго точечного заряда Q того же знака в точку, в которой расстояние между зарядами станет равным r2.
По определению, работа переменной силы при перемещении тела из точки 1 в точку 2: A = 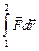 =
=  . В нашем случае угол a между направлением силы и направлением перемещения первого заряда равен нулю (заряды отталкиваются), а сама сила F описывается выражением, входящим в закон Кулона, поэтому
. В нашем случае угол a между направлением силы и направлением перемещения первого заряда равен нулю (заряды отталкиваются), а сама сила F описывается выражением, входящим в закон Кулона, поэтому
A =  =
= 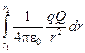 =
= 
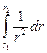 =
= 
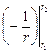 = =
= = 
 .
.
Последнее выражение можно интерпретировать, как убыль потенциальной энергии: A = WП1 - WП2. Полагая, что на бесконечности (при r → ∞ заряды практически перестают взаимодействовать, F → 0) потенциальная энергия равна нулю (то есть при r2 → ∞ WП2 → 0), получаем выражение для потенциальной энергии в точке 1 поля: WП1 = 
 . Такую же формулу можно записать для потенциальной энергии заряда q в любом другом месте поля, создаваемого точечным зарядом Q:
. Такую же формулу можно записать для потенциальной энергии заряда q в любом другом месте поля, создаваемого точечным зарядом Q:
WП = 
 . (8.1)
. (8.1)
Очевидно: потенциальная энергия WП численно равна работе A∞, которую необходимо совершить силам поля с тем, чтобы переместить положительный заряд из данной точки на бесконечность.
В электрическом поле, создаваемом не одним, а несколькими зарядами потенциальная энергия заряда q равна алгебраической сумме значений потенциальной энергии в полях, создаваемых каждым зарядом в отдельности:
WП = 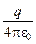
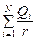 = qj (8.2)
= qj (8.2)
(здесь j – результирующий потенциал электрического поля в данной точке).
На основе данной формулы можно получить, что при перемещении заряда q из точки поля с потенциалом j1 в точку с потенциалом j2 силы поля совершают работу A = q(j1 - j2), или, введя обозначение j1 - j2 = U, запишем для работы сил поля
A = qU. (8.3)
Замечание: Символом U в разделе «электричество» принято обозначать падение напряжения на участке цепи. В общем случае (например, если рассматриваемый участок содержит батареи, аккумуляторы), понятия разность потенциалов и падение напряжения не совпадают. В электростатике, однако, мы не рассматриваем работу источников тока, и в этом случае отличия между данными понятиями нет: можно говорить, что U это разность потенциалов электрического поля в двух выбранных точках, а можно – что это падение напряжения (или напряжение) на участке между этими точками.
Замечание:
Если после перемещения в поле по замкнутому контуру l заряд q вернули в исходную точку (r1 = r2), работа сил электростатического поля окажется равной нулю, поскольку WП1 = WП2. Это можно отобразить так:
A = 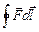 = 0.
= 0.
Из определения напряжённости электрического поля 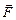 = q
= q  , следовательно,
, следовательно,
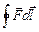 = q
= q  = 0, то есть в электростатическом поле
= 0, то есть в электростатическом поле
 = 0. (8.4)
= 0. (8.4)
В математике интеграл вида  называют циркуляцией вектора
называют циркуляцией вектора  , поэтому можно сказать: в электростатическом поле циркуляция вектора
, поэтому можно сказать: в электростатическом поле циркуляция вектора  равна нулю.
равна нулю.
8.1.2 Потенциал – энергетическая характеристика
электрического поля. Графическое отображение потенциала (эквипотенциальные линии)
С потенциальной энергией заряда тесно связана энергетическая характеристика электрического поля: потенциал j.
Потенциалом электрического поля в заданной точке называется отношение потенциальной энергии положительного пробного заряда, помещаемого в эту точку поля, к величине заряда:
j = 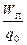 . (8.5)
. (8.5)
В СИ потенциал электрического поля измеряется в вольтах, очевидно, что 1 В = 1 Дж×Кл-1.
С учётом того, что WП = A∞, иногда говорят, что потенциал численно равен работе, которую должны совершить силы поля с тем, чтобы переместить единичный пробный заряд из данной точки поля в бесконечность.
Выражение для WП в поле точечного заряда мы вывели ранее – (8.1), поэтому, пользуясь определением, можем записать формулу для расчёта потенциала такого поля в точке, удалённой от заряда Q на расстояние r:
j = 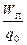 =
= 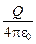
 . (8.6)
. (8.6)
Так же, как и напряжённости электрического поля, для потенциала справедлив принцип суперпозиции, однако, в отличие от напряжённости, которая является вектором, потенциал – скаляр, может быть как положительным, так и отрицательным, и поэтому принцип звучит так: потенциал электрического поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых каждым зарядом в отдельности.
Потенциал электрического поля можно отображать графически с помощью эквипотенциальных линий (и поверхностей) – линий, потенциалы во всех точках которых одинаковы. Их особенностями является то, что
– эквипотенциальные линии всегда замкнуты;
– эквипотенциальные поверхности и силовые линии всегда взаимно перпендикулярны.

Примеры картин эквипотенциальных линий приведены на рис. 8.1 и 8.2; силовые линии на этих рисунках проведены пунктиром.

8.1.3 Связь потенциала и напряжённости электрического поля
Если заряд q поместить в электрическое поле и затем отпустить его, то под действием сил поля, он начнёт двигаться и на малом первом участке пути dl вдоль силовой линии эти силы совершат работу
dA = 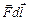 = q0
= q0 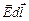 = q0Edl×cos0º = q0Edl.
= q0Edl×cos0º = q0Edl.
Но, поскольку работа сил поля равна убыли потенциальной энергии заряда, можно записать:
dA = -dWП
(напомним, что в математике знак дифференциала означает бесконечно малое приращение: из нового значения функции мы вычитаем предыдущее; в нашем случае речь идёт об убыли, то есть, наоборот, нужно вычесть последующее значение функции из предыдущего, отсюда возникает знак «минус» перед dWП).
Из определения потенциала следует, что dWП = q0dj, поэтому запишем: dA = q0Edl = -q0dj, то есть при перемещении вдоль силовой линии
E = -  . (8.7)
. (8.7)
Если вектор перемещения  разложить по осям координат X, Y, Z (единичные вектора по которым обозначим
разложить по осям координат X, Y, Z (единичные вектора по которым обозначим  ,
, 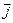 ,
,  ), связь между напряжённостью и потенциалом электрического поля может быть представлена в виде
), связь между напряжённостью и потенциалом электрического поля может быть представлена в виде
 = -gradj, (8.8)
= -gradj, (8.8)
где символ gradj означает вектор вида
gradj = 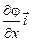 +
+ 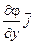 +
+  .
.
Соотношения (8.7) и (8.8) позволяют по заданной зависимости E(x, y, z) находить функцию j(x, y, z).
8.1.4 Теорема Гаусса для электрического поля в вакууме
Как мы уже отмечали, если хотя бы один из взаимодействующих зарядов нельзя считать точечным, равномерно заряженным шаром или сферой, для вычисления силы электростатического взаимодействия используют силовую характеристику поля – его напряженность в данной точке. Зная напряжённость, мы находим силу (  = q
= q  ), действующую на заряд q в этой точке, вычисляем его ускорение, определяем траекторию движения и т. д. Саму напряжённость
), действующую на заряд q в этой точке, вычисляем его ускорение, определяем траекторию движения и т. д. Саму напряжённость  можно рассчитать, пользуясь принципом суперпозиции, однако в ряде случаев в этих целях удобнее использовать теорему Гаусса.
можно рассчитать, пользуясь принципом суперпозиции, однако в ряде случаев в этих целях удобнее использовать теорему Гаусса.
Введём определение: если каждой точке пространства можно сопоставить некоторый вектор (например, – вектор 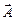 ), то, выбрав в этом пространстве некоторую поверхность S, можно говорить о потоке вектора
), то, выбрав в этом пространстве некоторую поверхность S, можно говорить о потоке вектора 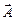 через эту поверхность S. Для вычисления потока поверхность S мысленно разбивают на много малых частей dS, каждой из которых сопоставляют вектор
через эту поверхность S. Для вычисления потока поверхность S мысленно разбивают на много малых частей dS, каждой из которых сопоставляют вектор 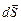 , по величине равный площади dS и направленный вдоль вектора нормали к поверхности выбранного участка (во всех случаях – к одной и той же стороне всей поверхности S). По определению потоком вектора
, по величине равный площади dS и направленный вдоль вектора нормали к поверхности выбранного участка (во всех случаях – к одной и той же стороне всей поверхности S). По определению потоком вектора 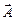 через элемент
через элемент 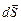 называется скалярное произведение этих векторов: dFA = (
называется скалярное произведение этих векторов: dFA = ( 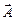
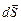 ) = AdS×cosa, где a – угол между векторами
) = AdS×cosa, где a – угол между векторами 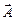 и
и 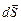 (см. рис. 8.3.а). Потоком вектора
(см. рис. 8.3.а). Потоком вектора 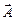 через всю поверхность S (рис. 8.3.б) называется интеграл вида
через всю поверхность S (рис. 8.3.б) называется интеграл вида
FA = 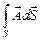
 |
В качестве вектора
 можно выбрать вектор силы (для описания поля сил), скорости (для описания движения частиц в струе жидкости), индукции магнитного поля и т. д. В теореме Гаусса для электрического поля в вакууме говорится о потоке FE вектора напряженности электрического поля
можно выбрать вектор силы (для описания поля сил), скорости (для описания движения частиц в струе жидкости), индукции магнитного поля и т. д. В теореме Гаусса для электрического поля в вакууме говорится о потоке FE вектора напряженности электрического поля  , при этом поток считается не через обычную поверхность, а через замкнутую, то есть разделяющую пространство таким образом, что проникнуть из одной его части в другую, не пронзив эту поверхность, невозможно.
, при этом поток считается не через обычную поверхность, а через замкнутую, то есть разделяющую пространство таким образом, что проникнуть из одной его части в другую, не пронзив эту поверхность, невозможно.
Сформулируем теорему.
Поток вектора напряжённости электрического поля через произвольную замкнутую поверхность равен деленной на электрическую постоянную e0 алгебраической сумме зарядов, охватываемых этой поверхностью:
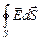 =
=  . (8.9)
. (8.9)
Заметим: формула не является альтернативой тексту теоремы, поскольку из (8.9) не следует, что замкнутая поверхность может иметь любую форму (в том числе – такую, которая нам удобна для проведения вычислений); кроме того, глядя на выражение (8.9) невозможно сказать, о каких зарядах qi идёт речь (учитываются только те, которые охватываются выбранной поверхностью!).
Вывод формул для напряжённости электрического поля с помощью теоремы Гаусса особенно прост в случаях полей, создаваемых симметричными заряженными объектами. Для вывода формул необходимо:
– Начертить рисунок с изображением заряженного тела и силовых линий создаваемого им электрического поля.
– Указать на рисунке точку, в которой мы будем рассчитывать величину напряжённости электрического поля, и провести сквозь эту точку силовую линию.
– Выбрать замкнутую поверхность, форма которой соответствовала бы симметрии задачи; поверхность должна проходить через выбранную точку.
– Посчитать поток вектора напряжённости электрического поля через выбранную поверхность (учитывая взаимную ориентацию отдельных частей поверхности и пронзающих их силовых линий).
– Определить, какой заряд охватывается выбранной поверхностью, после чего применить теорему Гаусса.
8.1.5 Примеры применения теоремы Гаусса для электрического поля в вакууме
а) Поле равномерно заряженной сферы
Рассмотрим сферу радиусом R и зарядом +Q. Она делит пространство на две область: внутри сферы (где зарядов нет) и снаружи от неё. Выражение для напряжённости создаваемого электрического поля получим для каждой из этих областей.
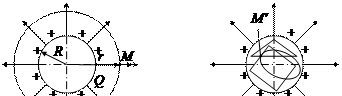 |
Для области вне сферы: рисуем чертёж, изображаем силовые линии, выбираем точку М, находящуюся на расстоянии r от центра сферы, проводим через неё одну из силовых линий, после чего выбираем замкнутую поверхность, соответствующую симметрии задачи и проходящую через эту точку. Очевидно, такой поверхностью будет сфера, центр которой совпадает с центром сферы, напряжённость электрического поля которой мы рассчитываем (рис. 8.4.а).
Теперь считаем поток вектора  через выбранную поверхность, учитывая, что нормаль к её любому участку, например, – с точкой M, совпадает с силовой линией, проходящей через этот участок (угол a, который входит в формулу для потока, везде равен нулю):
через выбранную поверхность, учитывая, что нормаль к её любому участку, например, – с точкой M, совпадает с силовой линией, проходящей через этот участок (угол a, который входит в формулу для потока, везде равен нулю):
FE = 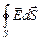 =
= 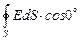 =
= 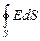
В силу симметрии выбранной поверхности напряжённость электрического поля в любой её точке должна быть одинаковой:
FE = 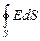 =
= 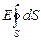 .
.
Но по определению интеграла 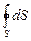 = S, где S = 4pr2 – площадь сферы; таким образом, FE = 4pr2E.
= S, где S = 4pr2 – площадь сферы; таким образом, FE = 4pr2E.
Применим теорему Гаусса: выбранной поверхностью охватывается весь заряд +Q, поэтому можно записать: 4pr2E = 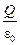 , или, другими словами, напряженность поля вне заряженной сферы
, или, другими словами, напряженность поля вне заряженной сферы
E =
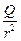 . (8.10)
. (8.10)
Для любой точки М¢в области, находящейся внутри заряженной сферы, можно выбрать сколь угодно много замкнутых поверхностей, проходящих через эту точку и при этом лежащих внутри заряженной сферы (рис. 8.4.б). По теореме Гаусса, так как ни одна из таких поверхностей не окружает заряд, то для них для всех FE = 0, независимо от формы. Другими словами, в этом случае 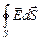 º 0 при любом S, а это возможно лишь если интеграл берётся от нуля, то есть внутри заряженной сферы E = 0.
º 0 при любом S, а это возможно лишь если интеграл берётся от нуля, то есть внутри заряженной сферы E = 0.
Некоторые примеры
- В физике, как правило, потенциал электрического поля равным нулю выбирается на бесконечности; в электротехнике за нулевой потенциал часто принимают поверхность Земли.
- У живых клеток в покое между внутренним содержимым клетки и наружным раствором существует разность потенциалов порядка 60 – 90 мВ.
- Разность потенциалов между катодом и анодом внутри электронно-лучевой трубки цветного телевизора достигает 25 кВ.
- Разность потенциалов между Землёй и ионосферой составляет 200 – 250 кВ.
Вопросы для повторения
1. Что называется потенциалом электрического поля? В каких единицах она измеряется в СИ? Как отображается графически?
2. Выведите формулу для потенциала электрического поля, создаваемого точечным зарядом.
3. В чём заключается принцип суперпозиции в случае потенциала электрического поля? Ответ поясните рисунком.
4. Запишите формулы, связывающие напряжённость и потенциал электрического поля и поясните смысл входящих в эти формулы величин.
5. Изобразите картины эквипотенциальных линий электростатических полей, создаваемых уединёнными точечными зарядами, близко расположенными разноимёнными зарядами, обкладками плоского электрического конденсатора.
6. Сформулируйте теорему Гаусса для электрического поля; запишите соответствующую формулу и поясните смысл входящих в формулу величин.
7. Продемонстрируйте, как применяется теорема Гаусса для вычисления напряженности электрического поля, создаваемого равномерно заряженной сферой.
Дата добавления: 2020-02-05; просмотров: 715;











