ЭЛЕКТРОСТАТИКА. ЧАСТЬ I

<7 8 91011 12 13 >

7.1 ОСНОВЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ

7.1.1 Законы Ньютона в релятивистской динамике

7.1.2 Энергия тела в СТО. Полная энергия, кинетическая энергия, энергия покоя

7.1.3 Связь энергии и импульса тела. Инварианты к преобразованиям Лоренца

7.2. ЭЛЕКТРОСТАТИКА. ЧАСТЬ I

7.2.1 Закон сохранения электрического заряда и закон Кулона – основополагающие законы электростатики

7.2.2 Напряженность электрического поля. Графическое отображение электрических полей

Некоторые примеры

Вопросы для повторения

7.1 ОСНОВЫ РЕЛЯТИВИСТСКОЙ ДИНАМИКИ

7.1.1 Законы Ньютона в релятивистской динамике

Вопросы, которые мы рассмотрели на предыдущей лекции, касались постулатов, лежащих в основе специальной теории относительности (СТО), и проблем, традиционно относящихся к кинематике поступательного движения (преобразований координат, времён, скоростей). Теперь обратим внимание на проблемы, относящиеся к динамике поступательного движения, и прежде всего, обсудим, в каком виде выполняются в рамках СТО законы Ньютона.

Первый закон Ньютона выполняется полностью, поскольку соответствует первому постулату Эйнштейна: все законы природы выполняются одинаковы образом в инерциальных системах отсчёта.

Второй закон Ньютона справедлив в общем виде:

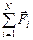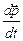= , (7.1)

где ,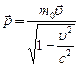

(здесь m₀ – масса покоящегося тела (масса покоя); с – скорость света в вакууме).

Ранее мы отмечали, что дробь 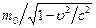в последней формуле зачастую интерпретируется, как релятивистская масса m тела, движущегося со скоростью u:

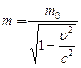, (7.2)

Что касается третьего закона Ньютона, то здесь требуются пояснения. Дело в том, что его классическая формулировка, в которой утверждается, что каждое действие носит характер взаимодействия, была выдвинута в то время, когда предполагалось, что взаимодействие переносится в пространстве мгновенно: достаточно что-то изменить в одном месте Вселенной, и в любом другом её месте это изменение можно почувствовать тут же. Но, согласно СТО, никакой сигнал не может распространяться быстрее света, то есть в передаче сигнала всегда есть запаздывание! Так, например, мы чувствуем воздействие далёких звёзд, свет от которых шёл к Земле миллиарды лет. Часть этих звёзд, возможно, уже прекратила существование, и в этом случае мы на них (наша Земля), конечно же, уже не действуем, хотя сами их действие ощущаем и будем ощущать ещё достаточно долго. Таким образом, в третьем законе Ньютона утверждение о том, что всякое действие носит характер взаимодействия, следует воспринимать с учётом запаздывания сигнала о воздействии одного тела на другое.

7.1.2 Энергия тела в СТО.

Полная энергия, кинетическая энергия, энергия покоя

По данным ЮНЕСКО, самой известной формулой физики XX века является соотношение

E = mc². (7.3)

В этой формуле m – релятивистская масса, см. (7.2); c – скорость света в вакууме, а E – полная энергия тела, включающая все виды энергии – кинетическую, потенциальную, энергию взаимодействия молекул и атомов, элементарных частиц, из которых они состоят… Фактически, соотношение (7.3) говорит об эквивалентности массы и энергии, в частности, поскольку, согласно закону сохранения полная энергия замкнутой системы не меняется со временем, не должна меняться и релятивистская масса такой системы.

Выражаемая формулой (7.3) связь массы с энергией уже находит практическое применение при создании атомного оружия и построении мирной ядерной энергетики.

Как и в классической динамике, мерой изменения энергии тела является работа, и, учитывая, что работа A, которую требуется совершить с тем, чтобы разогнать тело из состояния покоя до некоторой скорости, численно равна приобретенной при этом телом кинетической энергии W_К, можно получить формулу для кинетической энергии в релятивистской физике.

Если E = mc² = для тела, разогнанного до скорости u, то в состоянии покоя (при u = 0) масса m = m₀ (масса покоя) и полная энергия тела является энергией покоя E₀ = m₀c². Согласно определению, W_К = A = E - E₀, или

W_К = mc² - m₀c². (7.4)

Как видим, данное выражение и отдалённо не напоминает формулу вида W_K = 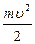, выведенную нами на одной из предыдущих лекций в предположении, что масса ускоряемого тела не меняется со временем. Тем не менее, следует помнить, что правильная теория должна допускать предельный переход от одних формул к другим при изменении соответствующих параметров задачи. В частности, продемонстрируем, что выражение (7.4) принимает вид, известный нам из классической физики, в области скоростей u << c. Для этого запишем формулу (7.4) более подробно:

W_К = mc² - m₀c² = - m₀c² = m₀c² .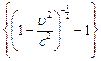

Далее используем известное из математики правило разложения в ряд по малому параметру выражение вида (1 + x)ⁿ, где ׀x׀ << 1:

(1 + x)ⁿ » 1 + nx. (7.5)[7]

В нашем случае x = - 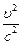(при u << c, действительно, ׀x׀ << 1); а n = - ½, то есть

W_К = m₀c² 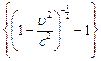= m₀c² = .

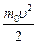Учитывая, что при u << c релятивистская масса m практически равна массе покоя m₀, мы, как и требовалось, получили классическое выражение для кинетической энергии поступательного движения тела постоянной массы.

7.1.3 Связь энергии и импульса тела.

Инварианты к преобразованиям Лоренца

Как мы отметили выше, полная энергия тела связана с его релятивистской массой соотношением E = mc². Преобразуем это выражение, возведя в квадрат правую и левую части и используя формулу для зависимости массы от скорости:

E² = m²c⁴ = = = 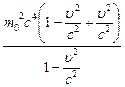m₀²c⁴ + 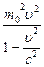c², или

E = . (7.6)

Пример 1:

При скорости объекта u << с (то есть при 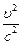<< 1)

E = = m₀c² = m₀c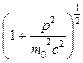² =

= m₀c² 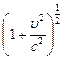» m₀c² 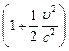= m₀c² + 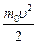= E₀ + W_К,

чего и следовало ожидать.

Пример 2:

Согласно второму постулату Эйнштейна в СТО кванты света (фотоны) в любой инерциальной системе отсчёта движутся со скоростью c, то есть не могут покоиться, и поэтому не обладают массой покоя: m₀ = 0. Поэтому для фотонов можно записать:

E = pc, или p = mc.

В заключение скажем несколько слов о основных законах природы, о которых мы говорили выше: о законах сохранения импульса, момента импульса, энергии. Согласно первому постулату Эйнштейна эти законы, так же, как и закон сохранения электрического заряда, в рамках СТО безусловно выполняются в любых инерциальных системах отсчёта. Кроме этого, следует отметить ряд параметров, которые должны оставаться неизменными при переходе от одной такой системы к другой (про них говорят, что они являются инвариантами по отношению к преобразованиям Лоренца).

К числу таких параметров относятся, например, скорость света в вакууме, масса покоя тела m₀ и связанная с ней энергия покоя E₀, а также выражение, которое следует из формулы (7.6) и отражает связь полной энергии тела и его импульса:

m₀²c⁴ = E² - p²c².

Нетрудно убедиться, что условию инвариантности соответствует выражение, связывающее координаты x₁ и x₂точки и моменты времени t₁ и t₂, в которые она имела эти координаты:

[c(t₂ - t₁)]² - (x₂ - x₁)² = [c(t₂¢ - t₁¢)]² - (x₂¢ - x₁¢)². (7.7)

В более общем случае, учитывая возможные изменения координат по всем трём осям X и Y и Z и используя следующее обозначение: (Dl)² = (x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)², можно записать:

(cDt)² - (Dl)² = (DS)² (7.8)

Входящий в эту формулу параметр DS называется пространственно-временным интервалом; о нём также можно сказать, что он является инвариантом по отношению к преобразованиям Лоренца. Само существование такого инварианта является подтверждением того, что пространство и время не являются независимыми сущностями, а неразрывно связаны друг с другом.

7.2 ЭЛЕКТРОСТАТИКА. ЧАСТЬ I

7.2.1 Закон сохранения электрического заряда и закон Кулона – основополагающие законы электростатики

Известно, что в природе существуют два вида электрических зарядов: положительные и отрицательные. Одноимённые заряды отталкиваются, разноимённые – притягиваются. Положительный заряд приобретает, например, стеклянная палочка, натёртая шёлком; отрицательный – эбонитовая палочка, натертая шерстью. До натирания палочки являются электронейтральными, в процессе натирания заряды одного знака остаются на палочке, другого знака – переходят на шёлк или шерсть. При этом происходит перераспределение зарядов, новых зарядов не возникает, а существовавшие ранее не исчезают.

Общий заряд тела определяется избытком или недостатком в нём зарядов того или иного знака. Так, например, в металлах этот заряд определяется количеством элементарных носителей электрического заряда – свободных электронов, частиц, которые имеют массу m »9,1×10^-³¹ кг и заряд e » - 1,6×10^-¹⁹ Кл (заряд электрона принимается отрицательным). Заряд электрона – минимальный, который может иметь свободная частица.

Тела могут обмениваться электрическими зарядами, отдавая их или принимая, однако при этом, согласно закону сохранения, алгебраическая сумма зарядов тел, входящих в замкнутую систему, не меняется со временем.

q₁ + q₂ + … + q_i + … + q_N = const. (7.9)

Термин «алгебраическая сумма» означает, что при суммировании необходимо учитывать знаки зарядов (сумма может оказаться и положительной, и отрицательной, и равной нулю); под замкнутой здесь понимается система, которая не обменивается зарядами с окружающей средой.

Вторым основополагающим законом, лежащим в основе учения об электричестве, является закон Кулона, согласно которому (как мы это уже говорили ранее):

– разноимённо заряженные тела притягиваются друг к другу, одноимённо заряженные – отталкиваются;

– сила взаимодействия заряженных тел прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними;

– если тела – однородно заряженные шары, сферы или их можно считать точечными зарядами (см. рис. 7.1), формулу закона Кулона можно записать в виде

F = 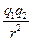. (7.10)

В этой формуле e₀ = 8,85×10^-¹² Ф/м– электрическая постоянная, q₁ – заряд первого тела, q₂ – заряд второго тела (на рис. 7.1 знаки зарядов противоположны), r – расстояние между центрами тел (шаров, сфер), e – диэлектрическая проницаемость среды, в которой находятся тела, F – сила их электростатического взаимодействия. Заметим: в полном соответствии с третьим законом Ньютона силы взаимодействия равны по величине и противоположны по направлению.

Закон Кулона – один из тех законов физики, которые не выводятся из каких-либо теоретических соображений, а отражают объективную реальность, и поэтому сами лежит в основе любых теорий, пытающихся объяснить «устройство» окружающего мира.

Закон Кулона можно применять и в тех случаях, когда заряженные тела не являются шарами, сферами или точечными зарядами. Пусть, например, одно из тел точечным считать нельзя. Тогда его необходимо мысленно разбить на N малых частей, для которых уже можно записать формулы вида (7.10), вычислить силы 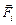, действующие со стороны этих частей на второе заряженное тело, а затем вычисленные силы векторно сложить. Говорят, что в данном случае используется принцип суперпозиции: искомая результирующая сила

= .

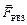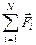Вычисления будут тем точнее, чем большим будет число N частей, на которые мы мысленно разбиваем первое тело; в предельном случае это число должно стремиться к бесконечности, а суммирование заменится интегрированием.

В общем случае подобные расчёты могут оказаться достаточно сложными, поэтому для нахождения сил, действующих на заряженные тела, в электростатике часто используют не сам закон Кулона, а формулы, в которых фигурирует вспомогательная силовая характеристика, называемая напряжённостью электрического поля.

7.2.2 Напряженность электрического поля.

Графическое отображение электрических полей

Напомним: если на тело в каждой точке пространства действует определённая сила, то говорят, что тело находится в поле сил. Если на заряженное тело со стороны других заряженных тел в каждой точке пространства действует сила Кулона, то можно говорить о поле таких сил, или об электрическом поле. По определению напряженностью электрического поля в заданной точке называется отношение силы 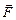, действующей на точечный зарядq₀, помещённый в эту точку, к величине этого заряда:

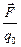= . (7.11)

Направление вектора совпадает с направлением силы, действующей на положительный точечный заряд q₀; в СИ напряжённость электрического поля измеряется в вольтах на метр: [ ] = 1 В×м^-¹; при этом 1 В×м^-¹ = 1 Н×Кл^-¹. Вольт – единица измерения электрического потенциала; обоснованность подобного выбора единицы измерения напряжённости электрического поля мы подтвердим позднее.

Замечание

Приведённое выше определение даёт нам практический способ нахождения . Так, например, если нас интересует напряженность электрического поля в данной точке комнаты, необходимо поместить в эту точку положительный заряд заданной величины q₀, измерить электрическую силу, которая на него будет действовать в этой точке (для этого можно использовать достаточно чувствительный динамометр), и, разделив F на q₀, вычислить величину Е. Направление совпадает с направлением силы .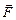

Задание:

Используя определение напряжённости электрического поля и формулу закона Кулона, убедитесь, что напряжённость электрического поля, создаваемого точечным зарядом q на некотором расстоянии r от него, рассчитывается по формуле

E =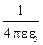 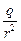. (7.12)

По такой же формуле рассчитывается напряжённость электрического поля, создаваемого заряженным шаром (или сферой) на расстоянии r от его центра при условии, что это расстояние больше радиуса шара (сферы).

Для напряжённости, так же, как и для силы, справедлив принцип суперпозиции: напряженность электрического поля , создаваемого в заданной точке системой заряженный тел, равна векторной сумме напряжённостей электрических полей, создаваемых в этой точке каждым телом в отдельности:

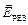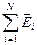= . (7.13)

Пример определения 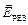путём векторного суммирования напряжённостей полей трёх зарядов поясняется рисунком 7.2.

Таким образом, если хотя бы одно из взаимодействующих заряженных тел – не точечное, не равномерно заряженные шар или сфера, напрямую формулу закона Кулона использовать нельзя, нужно выражать силу 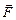, действующую на заряд q, через напряженность электрического поля , в котором заряд находится:

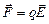. (7.14)

Саму же напряжённость следует заранее рассчитать, пользуясь уже рассмотренным принципом суперпозиции, применяя теорему Гаусса (о ней речь пойдёт позднее) и просто (если это возможно) заранее измерить с помощью соответствующих приборов.

Электрическое поле можно отображать графически с помощью силовых линий. Силовой называется линия, касательная в каждой точке к которой совпадает по направлению с силой, действующей в электрическом поле на точечный положительный заряд, помещаемый в эту точку.

Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных (или уходят в бесконечность). Очевидно, силовые линии не должны пересекаться, поскольку, если бы хотя бы пара линий пересеклась в какой-то точке поля, то в этой точке можно было бы провести две касательные (по одной к каждой линии), а, значит, однозначно определить направление действия кулоновской силы на помещаемый туда заряд было бы нельзя.

Примеры картин силовых линий полей, создаваемых отдельными зарядами и системами зарядов, приведены на рис. 7.3 – 7.5.

Принцип построения силовой линии поясняется рисунком 7.5. Пробный точечный заряд q₀ помещаем в некоторую точку поля, по принципу суперпозиции находим величину и направление результирующего вектора 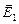в этой точке. Затем отпускаем заряд q₀ и даём ему возможность немного сместиться под действием сил поля. В новой точке фиксируем заряд, опять определяем величину и направление вектора напряжённости, вновь отпускаем заряд, позволив ему сдвинуться дальше, затем ещё раз останавливаем и ищем напряженность поля, и т. д. Определив направления векторов напряжённости на пути перемещения пробного заряда от +q₁ до -q₂, строим линию, к которой все эти вектора были бы касательными.

Это и будет искомая силовая линия (на рисунке изображены лишь три последовательных положения заряда q₀и три соответствующих вектора напряжённост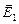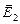и: , и ).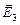

Некоторые примеры

- Один из проектов создания электронных пушек для уничтожения военных космических аппаратов подразумевает стрельбу по движущейся мишени пучком ускоренных электронов. После прохождения разности потенциалов в 10 МВ (или 10⁷ В) скорость электронов возрастает почти до 0,98c, что позволяет поражать цели на орбите вокруг Земли практически мгновенно.

- При столкновении протона и антипротона происходит их аннигиляция: они исчезают, но при этом рождаются два кванта электромагнитного излучения, суммарная энергия которых равна примерно 3×10^-¹⁰ Дж. При аннигиляции молекулы обычной воды и молекулы воды из антивещества энергии выделяется уже в 18 раз больше. Это означает, что при попадании в атмосферу земли метеорита из «антильда» массой всего в 1 г при его аннигиляции выделится энергия примерно 1,8×10¹³ Дж: в три с лишним раза больше, чем выделилось энергии при взрыве четырёхтонной атомной бомбы в Хиросиме.

- Средняя напряжённость электростатического поля нашей планеты (системы Земля – ионосфера) составляет примерно 100 В/м.

- Оценка и нормирование электростатических полей на рабочих местах осуществляется в зависимости от времени воздействия поля на работника. Так, при напряженности электрического поля менее 20 кВ/м время пребывания на рабочем месте не регламентируется, но уже в электростатических полях с напряженностью более 60 кВ/м нахождение персонала без специальных средств защиты не допускается вообще.

Вопросы для повторения

1. Выполняются ли законы Ньютона в рамках СТО?

2. Как рассчитывается кинетическая энергия в СТО?

3. Продемонстрируйте, что при малых скоростях объекта релятивистская формула для его кинетической энергии переходит в выражение, известное из классической механики.

4. Что имеется в виду, когда говорят, что некоторый параметр является инвариантом к преобразованиям Лоренца? Приведите примеры таких параметров.

5. Продемонстрируйте, что пространственно-временной интервал действительно является инвариантом к преобразованиям Лоренца.

6. Сформулируйте закон сохранения электрического заряда.

7. Сформулируйте закон Кулона; ответ поясните рисунком.

8. Что называется напряжённостью электрического поля? В каких единицах она измеряется в СИ? Как отображается графически?

9. В чём заключается принцип суперпозиции в случае напряженности электрического поля? Ответ поясните рисунком.

10. Изобразите картины силовых линий электростатических полей, создаваемых уединёнными точечными зарядами, близко расположенными разноимёнными и одноимёнными электрическими зарядами, обкладками плоского электрического конденсатора.

<7 8 91011 12 13 >

Дата добавления: 2020-02-05; просмотров: 443;

Поиск по сайту

Узнать еще