Лекция 10 ЭЛЕКТРОСТАТИКА. ЧАСТЬ IV
10.1 ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ (Часть 2)
10.1.1 Теорема Гаусса для электрического поля в диэлектрике
10.2 МЕТАЛЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
10.2.1 Напряжённость и потенциал электрического поля в уединённом проводнике
10.2.2 Электроёмкость уединённого проводника
10.2.3 Энергия уединённого заряженного проводника
10.2.4 Электрические конденсаторы. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Некоторые примеры
Вопросы для повторения
10.1 ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ (Часть 2)
10.1.1 Теорема Гаусса для электрического поля в диэлектрике
Как мы показали на предыдущих лекциях, теорема Гаусса позволяет вывести формулы для расчёта напряжённости электрического поля в вакууме. Но прямое использование данной теоремы для расчёта поля в диэлектрике осложняется необходимостью учёта вклада в суммарный заряд, охватываемый выбранной замкнутой поверхностью, всех зарядов молекул вещества, также охваченного этой поверхностью. Понятно, что в целом молекулы электронейтральны, но ведь при произвольном выборе поверхности часть из них будет «рассекаться» этой поверхностью на положительно и отрицательно заряженные части, вклад которых в общий заряд нам приходится учитывать.
Рассмотрим эту ситуацию подробнее на примере неполярного диэлектрика. Пусть такой материал, в который помещены N заряженных объектов (их заряды q1 ¸ qN мы будем называть свободными), находится в неоднородном электростатическом поле напряжённостью. В этом поле молекулы материала станут диполями, причём их дипольные моменты 
в каждой точке будут параллельны силовым линиям поля (рис. 10.1). Окружим некоторую область вещества замкнутой поверхностью (на рисунке её сечение обозначено BFJM на сером фоне), и подсчитаем заряд, охватываемый этой поверхностью.
Во-первых, эта поверхность охватывает свободные заряды, сумма которых равна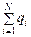 
. Во-вторых, поверхность охватывает заряды, связанные c диполями, однако, часть диполей целиком находится в охватываемой области, и их суммарный вклад в общий заряд равен нулю (на рисунке это диполи 2, 8, 9, 11). Часть диполей лежит вне охватываемой области, и поэтому их заряд также учитывать не нужно (диполи 3, 5, 10, 14).
Вблизи малого участка dS, в области которого поле можно считать практически однородным, суммарный заряд dQ, который соответствует диполям, лишь одной вершиной находящейся в охватываемой области (диполи 4, 12, 13), равен
dQ = -qndV, (10.1)
где n – концентрация диполей (их общее число в единице объёма), dV = l×cosa×dS – объём вблизи площадки dS, занимаемый зарядом, который следует учитывать, l – длина диполя, a – угол между вектором 
и внешней нормалью к dS. В формуле (10.1) учтено, что заряд, который мы учитываем, отрицателен.
Согласно теореме Гаусса, интегрируя по всей замкнутой поверхности, получим:
= 
+ 
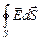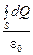, или
= + 
.
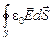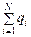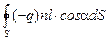Но произведение ql = pe, причём npe = P, где pe – электрический дипольный момент молекулы, а P – поляризованность вещества. Более того, по определению скалярного произведения и учитывая, что площадке dS соответствует вектор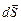 
, направленный по вектору внешней нормали, можно записать:
= - 
.
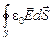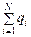Оба интеграла, входящие в эту формулу, берутся по одной и той же поверхности, поэтому их можно объединить:
= .
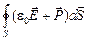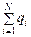Комбинация векторов напряжённости электрического поля и поляризованности, стоящая под знаком интеграла, обозначается символом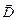 
и называется вектором электрического смещения:
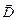= e0 + 
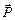. (10.2)
Формулировка же теоремы Гаусса приобретает вид: поток вектора электрического смещения через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью,
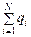= . (10.3)
Очевидно, что в вакууме, где нет никаких дипольных моментов и 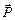= 0, формула приобретает уже знакомый нам вид.
На практике, описывая связь векторов 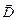и , обычно учитывают, что 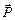= e0k , где k – диэлектрическая восприимчивость вещества (это мы показали на прошлой лекции). При этом
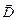= e0 + = e0 + 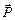e0k = (1 + k)e0 .
Сумма 1 + k обозначается буквой e и называется диэлектрической проницаемостью вещества, то есть
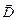= ee0 . (10.4)
Применяя теорему Гаусса, сформулированную для электрического поля в диэлектрике, и используя соотношение (10.4), можно вывести выражения для напряжённости электрического поля, создаваемого в этом диэлектрике равномерно заряженными сферой (вне сферы E =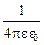
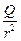),нитью (E = 
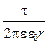), плоскостью (E = 
). Студентам предлагается сделать это самостоятельно.
10.2 МЕТАЛЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
10.2.1 Напряжённость и потенциал электрического поля
в уединённом проводнике
Согласно классической теории электропроводности, главным отличием диэлектриков от металлов является наличие в последних газа свободных электронов, оторвавшихся от атомов кристаллической решётки и способных свободно перемещаться по всему объёму образца. Направленное движение электронов (электрический ток) возникает под влиянием силы, действующей со стороны электрического поля, но если тока нет, то это означает, что нет и силы, а, значит, внутри проводника не должно быть электрического поля, EВНУТР = 0 (здесь EВНУТР – напряжённость электрического поля внутри проводника).
Принимая во внимание связь напряжённости электрического поля с потенциалом ( = -gradj), из условия, что EВНУТР = 0, получаем, что внутри проводника потенциал должен быть везде одинаков, j = const. Таким образом, в постоянном электрическом поле объём уединённого проводника и его поверхность эквипотенциальны.
Если проводник заряжен, заряды, отталкиваясь друг от друга, располагаются на его поверхности и больше не движутся (токов нет). Это означает, что вектор напряженности электрического поля не имеет компоненты, параллельной поверхности проводника, то есть силовые линии оказываются перпендикулярными этой поверхности. Распределение зарядов по поверхности может быть неравномерным: так, где есть выступы, плотность заряда s (и напряжённость создаваемого ими поля) оказывается выше, вблизи впадин, углублений s оказывается меньше.
Внесение даже нейтрального проводника в электрическое поле меняет картину силовых линий этого поля: свободные заряды, имеющиеся в проводнике, перераспределяются по его поверхности таким образом, чтобы компенсировать действие внешнего поля (и обеспечить выполнение условия EВНУТР = 0), – рис. 10.2. Данный эффект положен в основу электростатической защиты электронного оборудования: если защищаемый от внешних полей прибор со всех сторон окружить металлическим корпусом, последний станет играть экранирующую роль: перераспределившиеся по его поверхности заряды обеспечат нулевую напряжённость электрического поля в объёме, ограниченном этим корпусом.
10.2.2 Электроёмкость уединённого проводника
Если уединённому (расположенному вдалеке от других заряженных и проводящих тел) проводнику сообщить электрический заряд q, то приобретаемый им при этом потенциал j окажется связан с q прямой пропорциональной зависимостью: j ~ q. Коэффициент пропорциональности
C =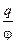 
(10.5)
называется электроёмкостью уединённого проводника, он не зависит ни от q, ни от j, а определяется лишь свойствами материала окружающей среды (диэлектрика), размером проводника и его формой (сокращенная аббревиатура МРФ).
Поясним сказанное выводом формулы для электроёмкости уединённого металлического шара (или сферы) радиусом RШ, находящегося в среде с диэлектрической проницаемостью e.
Сначала получим формулу для потенциала поверхности шара, с зарядом q. Как мы говорили ранее, это поверхность эквипотенциальна, силовые линии перпендикулярны к ней и при их мысленном продолжении проходят через центр шара (мысленном, поскольку поля внутри шара нет). В этом случае связь потенциала с напряжённостью удобно описывать не зависимостью = -gradj), а формулой, применяемой при движении вдоль силовой линии (в вдоль прямой, исходящей из центра шара: E = - 
. Кроме того, учтём, что напряжённость электрического поля вне равномерно заряженного шара описывается выражением E = .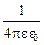
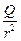При перемещении с поверхности шара на бесконечность должно выполняться соотношение:
= - 
= - 
= 
.
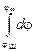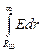Поскольку на бесконечности потенциал мы приняли равным нулю (j¥ = 0), можно записать:
jШ = 
. (10.6)
Теперь пришла пора использовать определение электроёмкости: C = 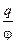, и получить искомую формулу
CШ = 4pee0RШ. (10.7)
Мы видим, что электроёмкость шара CШ действительно зависит от свойств материала окружающей среды (его e), размера шара (RШ) и его формы (мы явно воспользовались тем, что это именно шар, вспоминая формулу для напряжённости электрического поля).
В СИ электроёмкость измеряется в фарадах, 1 Ф = 1 Кл×В-1.
Формула 10.7 позволяет определить единицу измерения[8] электрической постоянной: [e0] = [CШ]/[RШ] = Ф/м
10.2.3 Энергия уединённого заряженного проводника
Ранее мы получили, что потенциальная энергия WП точечного заряда q, находящегося в вакууме на расстоянии r от другого точечного заряда Q, рассчитывается по формуле WП = 
. Нетрудно показать, что если заряды находятся в среде с диэлектрической проницаемостью e, формула принимает вид WП = 
.
Обозначим один заряд q1, а второй, соответственно, q2. Тогда
WП =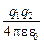 
= 
=
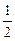
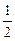= q1 
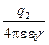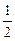+ q2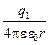 
= 
+ 
.
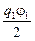Здесь j1 – потенциал поля, создаваемого первым зарядом в той точке, где находится заряд q2, и, наоборот, j2 – потенциал поля, создаваемого зарядом q2 в той точке, где находится заряд q1. Оба слагаемых равноценны: всё равно считать, который из зарядов находится в поле соседа, то есть энергия WП является общей потенциальной энергией данной системы зарядов.
Для потенциальной энергии системы, состоящей не из двух, а из N точечных зарядов q1, q2, … , qi, … , qN, можно записать:
WП =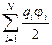 
. (10.8)
Такой системой можно считать поверхность имеющего заряд q проводника, предварительно разбив её на N достаточно малых частей. Однако, в отсутствие электрического тока, все точки проводника имеют одинаковый потенциал j, следовательно,
WП = =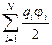 
= 
,
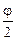
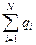Используя определение электроёмкости (10.5), выражение для энергии заряженного проводника, можно представить в виде:
WП = = 
= 
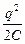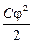. (10.9)
10.2.4 Электрические конденсаторы. Электроёмкость
конденсатора. Электроёмкость плоского конденсатора
Электрическим конденсатором называется система, состоящая из двух близко расположенных проводников. Чаще всего в электрических схемах конденсаторы соединены таким образом, что при накоплении на одном из них заряда +q, заряд на другом оказывается равным -q. Если принять потенциал первого проводника равным j1, а потенциал второго, равным j2, то электроёмкостью конденсатора будет называться отношение
C = 
. (10.10)
С учётом введённого ранее обозначения U = j1 - j2, выражение (10.10) приобретает вид:
C = 
. (10.11)
Так же, как и в случае уединённого проводника, электроёмкость конденсатора зависит от свойств материала окружающей среды (М), размеров проводников (Р), и их формы (Ф), в том числе – от геометрии их взаимного расположения в пространстве, и также измеряется в фарадах.
Следует особо обратить внимание на то, что электроёмкостью обладает система из двух любых близко расположенных проводников, а не только тех, которые входят в состав используемых в радиосхемах конденсаторов. Центральная жила кабеля и его заземляющая оплётка – электрический конденсатор, провод линии электропередачи и земля – тоже и т. д. То, что такие системы обладают собственной электроёмкостью, необходимо учитывать при расчёте токов утечки (как известно, конденсатор проводит переменный электрический ток), возможных наводок паразитных сигналов в цепях работающей аппаратуры.
В общем случае расчёт электроёмкости системы из двух проводников может быть весьма затруднителен, поэтому на практике конденсаторы изготавливают из таких материалов, таких размеров и формы, для которых расчёт C достаточно прост. В качестве примера покажем, как рассчитывается электроёмкость плоского конденсатора: системы из двух параллельных разноимённо заряженных проводящих (металлических) плоских пластин, линейные размеры которых много больше расстояния d между ними. Площадь каждой из пластин S; между пластинами находится изолирующая среда с диэлектрической проницаемостью e.
Полагая, что в наших условиях каждую заряженную пластину можно считать плоскостью с поверхностной плотностью заряда +s и -s соответственно, запишем формулу для напряжённости электрического поля в области между пластинами: E = (студентам предлагалось вывести её самостоятельно по аналогии с формулой для напряжённости поля в области между двумя параллельными, находящимися в вакууме плоскостями E =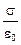 
).
Ранее мы рисовали картину силовых линий внутри плоского конденсатора: они перпендикулярны пластинам, поэтому, выбрав ось координат X так, как это показано на рис. 10.3, и вспомнив связь E с j, запишем, что вдоль силовой линии E = -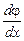 
.
Из этого выражения следует:
dj = -Edx, или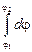 
= - 
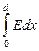, то есть j2 - j1 = - d.
По ходу дела отметим полученное нами и очень полезное в практическом отношении соотношение: для плоского конденсатора
E =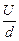 
. (10.12)
Поскольку U = j1 - j2, а s = q/S, где q – заряд одной пластины, можно записать, что U =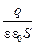 
d. С учётом определения C = q/U, мы получаем искомую формулу для расчёта электроёмкости плоского конденсатора:
C =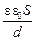 
. (10.13)
Расчёт электроёмкости конденсаторов других конструкций (цилиндрических, сферических и т. д.) ведётся по аналогичному принципу: сначала выводим формулу для расчёта E (например, – с помощью теоремы Гаусса), затем, используя связь E с j, находим разность j1 - j2 между проводниками-обкладками конденсатора, после чего применяем формулу-определение C.
Из формулы (10.13) можно легко получить единицу измерения электрической постоянной e0 (Ф/м).
В заключение отметим: в электрических схемах конденсаторы могут соединяться друг с другом и с другими элементами цепи разным образом. О способах соединения простейших элементов электрических цепей и о методах соответствующих расчётов будет рассказано на практических занятиях.
Некоторые примеры
- Электроёмкость планеты Земля составляет примерно 700 мкФ.
- Для экранировки внешнего электростатического поля в обычных условиях достаточно слоя металла толщиной в один – два атомных слоя.
Вопросы для повторения
1. Что называется вектором электрического смещения? В каких единицах его величина измеряется в СИ?
2. Сформулируйте теорему Гаусса для электрического поля в диэлектрике; запишите соответствующую формулу и поясните смысл входящих в формулу величин.
3. Продемонстрируйте, как применяется теорема Гаусса для вычисления напряженности электрического поля в диэлектрике в случае полей, создаваемых: а) равномерно заряженной сферой; б) равномерно заряженной тонкой бесконечной прямой нитью; в) равномерно заряженной плоскостью; г) двумя параллельными разноимённо заряженным плоскостями.
4. Что называется электроёмкостью уединённого проводника? От чего она зависит? В каких единицах измеряется в СИ?
5. Выведите формулу для расчёта электроёмкости металлического шара.
6. Что называется электроёмкостью конденсатора? От чего она зависит? В каких единицах измеряется в СИ?
7. Выведите формулу для расчёта электроёмкости плоского конденсатора.
Дата добавления: 2020-02-05; просмотров: 430;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
