Лекция 6 МЕХАНИКА. ЧАСТЬ VI

6.1 ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (СТО)

6.1.1 Принцип относительности Галилея. Постулаты Эйнштейна

6.1.2 Преобразования Галилея. Неинерциальные системы отсчёта

6.1.3 Преобразования Лоренца

6.1.4 Следствия из преобразований Лоренца

Некоторые примеры

Вопросы для повторения

6.1 ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (СТО)

6.1.1 Принцип относительности Галилея.

Постулаты Эйнштейна

Итак, мы отметили, что, все законы природы инвариантны относительно инерциальных систем отсчёта. В классической физике подобное утверждение впервые высказал Галилей: согласно принципу относительности Галилея все законы классической механики не меняются при переходе от одной инерциальной системы отсчёта к другой.

Надо сказать, что физика, как наука, началась именно с Галилея: он был первым, поставившим на первое место в научных дискуссиях не умозрительные построения, основанные на чистой логике и «здравом смысле», а результаты реальных измерений. Заметим: во времена Галилея не существовало специальных измерительных приборов, ни научной общественности, с которой можно было бы вести полноценную дискуссию, ни, конечно же, научных журналов. Единственным способом ознакомить общественность со своими взглядами было написание литературных произведений, в канву которых вплетались бы научные дискуссии героев: читатель, следя за сюжетом, поневоле был вынужден знакомиться с их высказываниями (выражающими главные научные идеи автора), спорами, и, в конце концов, сам усвоить эти идеи. Именно в таком ключе Галилеем и была написана в 1632 году книга «Диалоги», в которой был изложен, в частности, принцип относительности. В этой книге автор на различных примерах показывает, что никакими механическими опытами, поставленными внутри движущейся равномерно и прямолинейно системы отсчёта, невозможно определить, движется ли эта система, или покоится.

На 250 лет позже появилась более общая теория, которая получила название специальной теории относительности (СТО)[5]. На английском языке слово «относительность» звучит «relativity», и поэтому в литературе по данной тематике часто звучат термины «релятивизм», «релятивистский» и т. д.

В основе СТО лежат два постулата, выдвинутые А. Эйнштейном.

Согласно первому постулату все законы природы инвариантны относительно инерциальных систем отсчёта. Другими словами, никакими опытами (включая всевозможные химические реакции, биологические процессы, физические явления) нельзя определить, движется ли равномерно прямолинейно объект относительно наблюдателя, или это сам наблюдатель движется равномерно прямолинейно относительно объекта: инерциальные системы отсчёта полностью равноценны.

Согласно второму постулатускорость света в вакууме одинакова во всех инерциальных систем отсчёта и не зависит от того, движутся ли источник света и приёмник или покоятся.

Из СТО также следует, что при переходе от описания объекта в одной инерциальной системе к описанию в другой системе, ряд параметров измениться не должен. К числу таких параметров (инвариантов) помимо скорости света в вакууме относятся масса покоя объекта, его электрический заряд и некоторые другие.

Если первый постулат обычно воспринимается без возражений (к сходному по формулировке принципу относительности Галилея люди привыкли уже достаточно давно), то второй постулат и связанное с ним утверждение о том, что скорость света в вакууме – максимально возможная скорость в природе до сих пор является достаточно удивительным. Ведь если принять этот постулат, то тут же оказывается, что должно выполняться его следствие: время в разных инерциальных системах отсчёта течёт по-разному!

Рассмотрим пример. Пусть в центре ракеты, движущейся со скоростью 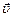относительно земли, установлена лампочка Л, а в салоне на равных расстояниях от этой лампочки – два фотоприёмника ФП-1 и ФП-2 (рис. 6.1). При включении лампы пилот отметит, что оба фотоприёмника срабатывают одновременно, ведь лампа равноудалена от обоих фотоприёмников. Однако наблюдателю, находящемуся на Земле покажется, что это не так: ведь ФП-1 движется навстречу лучу света, и поэтому сработает раньше, чем ФП-2, поскольку луч света движется ему вдогонку. Другими словами, события, являющиеся одновременными в одной системе отсчёта, в другой таковыми не являются, то есть время в этих системах действительно течёт по-разному!

6.1.2 Преобразования Галилея. Неинерциальные системы отсчёта

В классической механике молчаливо предполагается, что ход времени одинаков во всех системах отсчёта. Этот факт нашёл отражение в системе уравнений, которые носят название преобразования Галилея и позволяют перейти от координат тела в одной системе отсчёта к координатам этого же тела в другой системе, движущейся относительно первой.

Рассмотрим простейший случай: система отсчёта X¢Y¢Z¢ движется равномерно прямолинейно относительно системы XYZ с постоянной скоростью u₀ вдоль оси OX (рис. 6.2). Пусть в начальный момент времени (t = 0) все оси координат полностью совпадали. Тогда, согласно законам кинематики, координаты x¢, y¢, z¢ некоторой точки А, являющейся неподвижной в системе X¢Y¢Z¢, в любой другой момент времени t оказываются связанными с координатами x, y, z этой же точки в системе XYZ следующими соотношениями:

x = x¢ + u₀t

y = y¢ (6.1)

z = z¢

Очевидно: если бы система X¢Y¢Z¢ двигалась прямолинейно равномерно относительно системы XYZ произвольным образом, соответствующие преобразования выглядели бы так:

x = x¢ + u_0xt

y = y¢+ u_0yt (6.2)

z = z¢+ u_0zt,

где u_0x, u_0y и u_0z – компоненты скорости системы X¢Y¢Z¢ относительно системы XYZ.

Продифференцировав правые и левые части уравнений (6.2) по времени, получим преобразования Галилея для скорости точки А в случае, если она движется равномерно прямолинейно и относительно обеих систем отсчёта:

u_x = u_x¢ + u_0x

u_y = u_y¢+ u_0y (6.3)

u_z = u_z¢+ u_0z,

Еще одно дифференцирование по времени и учёт того, что u_0x, u_0y и u_0z неизменны, позволяют получить соотношение между компонентами ускорения:

a_x = a_x¢

a_y = a_y¢ (6.4)

a_z = a_z¢,

то есть если точка А и начнёт двигаться с ускорением относительно инерциальных систем отсчёта X¢Y¢Z¢ и XYZ, то это ускорение будет одинаковым в обеих системах. Но поскольку для тела постоянной массы 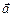= 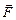/m, то это означает, что и сила, вызывающая это ускорение, одинакова в обеих системах отсчёта. Другими словами, мы, вслед за Галилеем, делаем вывод о том, что все явления механики должны протекать одинаково в любых системах отсчёта, движущихся друг относительно друга равномерно прямолинейно или покоящихся.

Если бы система X¢Y¢Z¢ двигалась относительно XYZ с ускорением 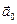, компоненты которого обозначим a_0x, a_0y и a_0z, то для координат, компонент скорости и ускорения точки А следовало бы записать:

x = x¢ + u_0xt + a_0xt²/2

y = y¢+ u_0yt + a_0yt²/2

z = z¢+ u_0zt + a_0zt²/2

u_x = u_x¢ + u_0x + a_0xt

u_y = u_y¢+ u_0y + a_0yt

u_z = u_z¢+ u_0z + a_0zt

a_x = a_x¢ + a_0x

a_y = a_y¢ + a_0y

a_z = a_z¢ + a_0z.

Из последних трёх уравнений следует, что для описания поведения точки А в системе отсчёта X¢Y¢Z¢, движущейся с ускорением (то есть – неинерциальной) наблюдателю, движущемуся вместе с этой системой, приходится предполагать, что в ней на точку действует добавочная сила 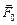= -m 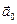. Подобные «нереальные» силы, которые приходится вводить в формулы только из-за того, что наблюдатель находится в неинерциальной системе отсчёта, называются силами инерции. Типичный пример силы инерции – «сила», которая «отбрасывает» человека назад при старте автомобиля: человеку, стоящему на тротуаре понятно, что никто пассажира не толкает назад, но самому пассажиру кажется, что его какая-то сила «вжимает» в кресло, пока автомобиль ускоряется.

Использование понятия сил инерции в ряде случаев позволяет проще записывать уравнения динамики и быстрее находить ответы в соответствующих задачах.

6.1.3 Преобразования Лоренца

Если учесть постулат Эйнштейна об инвариантности скорости света при переходе от одной системы отсчёта к другой, то системы уравнений, позволяющих осуществлять пересчёт координат и скоростей точки при переходе от одной инерциальной системы отсчёта к другой, существенно меняются. Соответствующие формулы носят название преобразований Лоренца. Лоренц впервые получил их, решая задачу о том, как описать изменение электрического и магнитного полей при переходе от системы отсчёта, в которой заряды покоятся (электростатика) к системе, в которой они движутся с постоянной скоростью (их можно интерпретировать, как постоянные токи). Любопытно, что уравнения были написаны до создания Эйнштейном теории относительности, но Лоренц интерпретировал их просто как удобный метод вычислений. Эйнштейн же, опираясь на работы Лоренца и ряда других авторов, выдвинул гораздо более сильную идею – данные преобразования не просто «математический фокус», ценный в практическом отношении метод расчётов: они отражают глубинные свойства окружающего нас мира!

Перед тем, как записать систему уравнений, позволяющих выполнять как прямые, так и обратные преобразования Лоренца для координат, вновь представим себе, что система отсчёта X¢Y¢Z¢ с постоянной скоростью 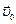движется вдоль оси X относительно системы отсчёта XYZ. В начальный момент времени (t = t¢ = 0, где t – показания часов в системе XYZ, t¢ – в системе X¢Y¢Z¢) оси систем координат совпадали; точка А неподвижна в системе отсчёта X¢Y¢Z¢ (рис. 6.3). Ниже записаны системы (6.5) и (6.6) преобразований Лоренца для рассматриваемого случая.

Прямые преобразования Лоренца для координат и времени

x =

y = y¢

z = z¢ (6.5)

t =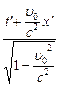

Обратные преобразования Лоренца для координат и времени

x¢ =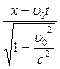

y¢ = y

z¢ = z (6.6)

t¢ =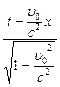

В классической механике Ньютона Вселенная рассматривается как бесконечное пространство, в каждой точке которого время течёт одинаково, и уж, тем более, независимо от того, движутся ли рассматриваемые системы отсчёта друг от друга или покоятся. Согласно СТО, дело обстоит принципиально иначе: t ¹ t¢, то есть нельзя говорить отдельно о пространстве и отдельно – о времени, они представляют собой единую систему, пространственно-временной континуум. В этом смысле нашу Вселенную следует считать не трёх-, а четырёхмерной, где состояние любого объекта описывается совокупностью четырёх взаимосвязанных переменных – трёх координат и времени. Другими словами, вопросы «где?» или «когда?» в СТО не имеют особого смысла, корректен лишь вопрос «где и когда?». Правда, в привычных нам условиях скорость реальных объектов много меньше скорости света в вакууме (c » 3×10⁸ м/с), то есть u₀ << с, и u₀/с » 0. Тогда t = t¢, системы уравнений (6.5) и (6.6) становятся идентичными и переходят в систему (6.1). Таким образом, в нашей повседневной жизни мы с успехом можем пользоваться динамикой Ньютона и полагать при этом, что время везде течёт одинаково.

Вернёмся к преобразованиям Лоренца.

Если точка А не неподвижна, а движется с постоянной скоростью u_x¢в системе отсчёта X¢Y¢Z¢, то, учитывая, что, по определению u_x = 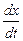, а u_x¢ = 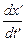, применяя формулы (6.5) и (6.6), можно вывести правило сложения скоростей в СТО:

u_x = 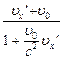. (6.7)

В частности, если точка А движется вдоль оси X¢ со скоростью света (u_x¢ = с), и при этом сама система отсчёта X¢Y¢Z¢ движется с такой же скоростью вдоль оси X (u₀ = с), то скорость точки А относительно системы отсчёта XYZ будет не u = с + с = 2с, как казалось бы на первый взгляд, а u_x = (с + с)/ 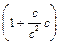= c, что находится в полном соответствии со вторым постулатом Эйнштейна в СТО.

6.1.4 Следствия из преобразований Лоренца

Из преобразований Лоренца вытекает ряд следствий, которые допускают экспериментальную проверку и, тем самым, могут свидетельствовать о том, насколько теория Эйнштейна соответствует действительности.

а) Сокращение длины движущихся объектов

Пусть объект, имеющий длину l₀ в системе отсчёта X¢Y¢Z¢, (рис. 6.4) движется вместе с этой системой со скоростью u₀ относительно системы XYZ вдоль оси X. Очевидно при этом, что l₀ = x₂¢ - x₁¢. Но длину объекта l можно измерить и в системе XYZ. Для этого в один и тот же момент времени t следует засечь координаты начала и конца объекта: l = x₂ - x₁. Используя обратное преобразование Лоренца для координаты x¢ (именно в него входит нужное время t), получим:

l₀ = x₂¢ - x₁¢ = 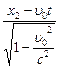- = = 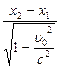, или

l = l₀ . (6.8)

Поскольку < 1, l < l₀, то есть, объект как бы «сокращается» в размерах относительно неподвижного наблюдателя вдоль направления своего движения[6]. Изменения размеров в двух других направлениях при этом не происходит.

б) Изменение длительности процесса

Пусть в одной и той же точке с координатой x¢ в движущейся системе отсчёта произошли два события, разделённые интервалом времени t₀ = t₂¢ - t₁¢. С точки зрения наблюдателя, находящегося в системе отсчёта XYZ этот интервал составляет t = t₂ - t₁. Используя обратное преобразование Лоренца для координаты x¢ (именно в него входит нужное время t), получим:

t = t₂ - t₁ = 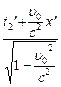- 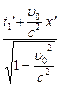= = 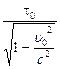, или

t = 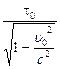. (6.9)

Поскольку < 1, t > t₀, то есть из формулы (6.9) следует, что длительность какого-либо события, происходящего с телом, минимальна в той системе отсчёта, в которой тело покоится. Чем быстрее тело движется, тем дольше длится это событие с точки зрения наблюдателя, мимо которого пролетает тело.

Последнее соотношение получило непосредственное экспериментальное подтверждение. Под действием солнечного излучения в верхних слоях атмосферы Земли рождаются элементарные частицы мюоны. Эти частицы нестабильны, они распадаются самопроизвольно на электрон (или позитрон) и два нейтрино. Среднее время жизни, измеренное в условиях, когда они неподвижны (или движутся с малой скоростью), составляет всего лишь 2·10^-6 с. На первый взгляд, даже двигаясь со скоростью света, мюоны за это время способны пролететь не более 600 м. Однако, как показывают наблюдения, мюоны, хотя и образуются на высоте 20 ¸ 30 км, всё же успевают в значительном количестве достигнуть земной поверхности. Это объясняется тем, что 2·10^-6 с – собственное время жизни мюона, то есть время t₀, измеренное по часам, движущимся вместе с ним. Время t, отсчитанное по часам экспериментатора, связанного с Землей, оказывается гораздо большим (скорость мюона близка к с). Поэтому нет ничего удивительного в том, что этот экспериментатор наблюдает пробег мюона, значительно больший 600м.

Отметим, что с позиции самого мюона, хотя его время существования и невелико, малым для него оказывается расстояние, пролетаемое до поверхности Земли (имеет место лоренцево сокращение длины).

С замедлением течения времени в движущейся системой отсчёта связан так называемый парадокс близнецов. Поскольку об этом парадоксе довольно часто вспоминается в научно-популярной и фантастической литературе, имеет смысл рассмотреть его подробнее. Напомним, что парадокс – это неожиданное положение, находящееся в видимом противоречии с общепринятыми понятиями.

Представим себе, что на Земле одновременно родились два брата – близнеца, один из которых в зрелом возрасте стал космонавтом и собрался полететь в межзвёздную экспедицию. До старта ракеты биологический возраст близнецов был одинаковым, поскольку оба всю жизнь провели на Земле и двигались со скоростями, много меньшими с. После старта космонавт будет двигаться с большой скоростью, а, следовательно, с точки зрения близнеца, оставшегося на Земле, его старение будет происходить медленнее. Это еще не парадокс, а простое следствие преобразований Лоренца.

Теперь сделаем еще один шаг в размышлениях: с точки зрения космонавта неподвижной можно было бы считать ракету, это Земля улетала из-под ног, и, следовательно, это землянин должен будет стариться медленнее! Итак, казалось бы, всё зависит от точки зрения, разницы – никакой. Однако, несмотря на кажущуюся равноценность систем отсчёта «ракета» и «Земля», после возвращения домой окажется, что всё же именно космонавт состарится меньше брата. Вот в этом и заключается видимое противоречие, парадокс.

Данный парадокс возник из-за того, что мы посчитали обе системы отсчёта равноценными. Но это не так: разгоняясь до околосветовой скорости, затормаживая у звезды, разворачиваясь, вновь разгоняясь по направлению к Земле, а затем – затормаживая для посадки, ракета оказывается неинерциальной, движущейся с ускорением системой отсчёта. Неинерциальность (это можно строго показать, используя математический аппарат СТО), как раз и приводит к тому, что общее время между стартом и возвращением ракеты для космонавта всё же окажется меньше, чем для земного наблюдателя.

Подобные эксперименты уже проводились в наше время: сравнивались показания часов, остававшихся на Земле, и запускавшихся в космос на спутниках. И хотя скорости современных космических аппаратов далеки от световых, различие в показаниях часов в земной лаборатории и возвращаемых на Землю после достаточно длительного полёта фиксируется вполне уверенно.

Некоторые примеры

- Учитывая, что среднее расстояние от Земли до Солнца составляет 150000000 км (это расстояние называется 1 а. е. – астрономическая единица), можно оценить время, за которое свет, испущенный нашим светилом, достигает земной поверхности: около 500 с или 8,3 мин.

- До самой близкой к Солнцу соседней звезды (Альфа Центавра) свет идёт примерно 4,4 года. Если полететь к этой звезде на космическом корабле, движущемся со скоростью 0,99с, то для космонавта полёт туда и обратно займёт примерно 9 лет. На Земле при этом пройдёт более 60 лет…

- По современным представлениям средний диаметр Вселенной составляет около 156 млрд. световых лет.

- Даже у аппарата, движущегося с третьей космической скоростью (16,6 км/с), лоренцево сокращение длины не превышает 1,5×10^-9 %.

Вопросы для повторения

1. Сформулируйте постулаты Эйнштейна в СТО. Чем формулировка первого постулата отличается от формулировки принципа относительности Галилея?

2. Приведите пример ситуации, которая говорит о том, что время в системах отсчёта, движущихся относительно друг друга, течёт неодинаково.

3. Каков смысл преобразований Галилея и Лоренца (что с их помощью можно определить)?

4. Приведите пример применения правила сложения скоростей в СТО.

5. Какие следствия вытекают из преобразований Лоренца?

6. Приведите пример эксперимента, для объяснения результатов которого необходимо привлекать преобразования Лоренца.

7. В чём заключается парадокс близнецов?

Оцените время, которое пройдёт на Земле за время космической экспедиции к Сириусу (до него примерно 8,6 световых лет пути) со средней скоростью 0,99 от скорости света.