Всякое действие носит характер взаимодействия; силы взаимодействия равны по величине и противоположны по направлению.

<1 2 345 6 7 >

Пример: Тело, подвешенное на нити, на пружине, лежащее на твёрдой поверхности, плавающее в жидкости действует на свою опору (нить, пружину, твёрдую поверхность, жидкость) с некоторой силой .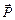

Сила 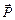, с которой тело действует на опору, называется весом тела.

Вес и сила реакции опоры приложены к разным телам и поэтому не могут уравновешивать друг друга!

На рис. 2.2.а) изображен кубик, лежащий на полу. Вес – это сила 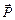, приложенная к поверхности пола; под действием этой силы пол немного прогибается. В свою очередь, пол действует на нижнюю часть тела с силой 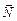(сила реакции опоры) – рис. 2.2.б). Кроме силы 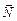на тело действует сила тяжести , приложенная к центру кубика – рис. 2.2.в). Поскольку кубик не вращается, его можно считать материальной точкой, к которой приложены всего две силы: 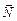и – рис. 2.2.г), причём в состоянии покоя должно выполняться условие:

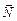+ = 0. (2.6)

Так как по третьему закону Ньютона

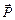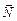= - , (2.7)

то это означает, что в состоянии покоя

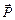= , (2.8)

Если же кубик движется с ускорением 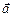(лежит на полу движущейся с ускорением кабины лифта), согласно второму закону Ньютона для него следует записать:

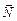+ = m 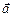, (2.9)

что, с учётом формулы (2.8), означает:

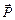= - m 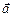. (2.10)

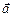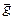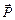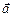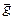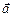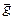Если вектор направлен туда же, куда и вектор , вес тела будет меньше силы тяжести (при = вес вообще исчезнет, наступит состояние невесомости). Если же вектора и направлены в противоположные стороны, возникает состояние перегрузки: вес тела оказывается больше его силы тяжести.

2.2.4 Закон Всемирного тяготения

Как мы уже говорили, в природе существуют четыре вида фундаментальных взаимодействий, одним из которых является гравитационное. В основе классической теории гравитации лежит открытый Ньютоном закон Всемирного тяготения, согласно которому:

– все тела в природе притягиваются друг к другу;

– сила притяжения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;

– если тела – однородные шары, сферы или их можно считать точечными, справедлива формула (см. рис. 2.3)

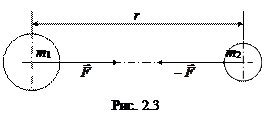F =G. (2.11)

В этой формуле G = 6,67×10^-¹¹м³×кг^-¹с^-² – гравитационная постоянная, m₁ – масса первого тела, m₂ – масса второго тела, r – расстояние между центрами тел (шаров, сфер), F – сила их гравитационного притяжения.

С некоторыми примерами применения этого закона мы встретимся позднее.

2.2.5 Примеры сил. Рекомендации к решению стандартных

задач по физике

· Если в задаче встречается слово «сила», следует вспомнить формулу второго закона Ньютона. При этом если масса тела, о котором идёт речь в задаче, постоянна, то:

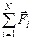= m 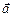. (2.12)

Далее необходимо:

– на чертеже изобразить все силы, действующие на тело, о котором идёт речь в задаче;

– начертить оси координат (одну из осей удобно направлять вдоль направления вектора ускорения тела );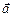

– изобразить проекции всех сил на выбранные оси;

– формулу (2.12) переписать для проекций сил.

· Если в задаче идёт речь о весе тела, для её решения следует переходить от веса к силе реакции опоры:

. (2.13)

Это связано с тем, что к телу приложена именно сила реакции опоры, а не вес, то есть в формуле (2.12) должна фигурировать сила 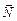, а не .

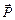· Если в задаче идёт речь о коэффициенте трения скольжения, для её решения следует записать формулу

F_ТР = mN, (2.14)

где F_ТР – сила трения скольжения, N – сила реакции опоры, m – коэффициент трения скольжения (зависит, прежде всего, от природы трущихся тел).

· Если в задаче идёт речь о пружине, для её решения следует записать формулу:

F_УПР = -kx, (2.15)

где F_УПР – сила упругости, с которой пружина действует на объект; x – смещение объекта от положения равновесия, k – коэффициент жёсткости пружины, который зависит от свойств материала, из которого изготовлена пружина, от её размеров и формы[2].

При решении задач полезно помнить, что коэффициент жёсткости k входит также в выражение для потенциальной энергии упруго деформированной пружины W_П = ½kx², которое мы выведем на одной из следующих лекций, а также в формулу для периода гармонических колебаний тела на пружине (пружинного маятника) T = 2p (её мы выведем в начале следующего семестра).

· Если в задаче идёт речь оспутниках, планетах, других космических объектах, для её решения необходимо записать формулу (2.11) закона Всемирного тяготения.

· Если в задаче идёт речь о теле, погружённом в жидкость (газ), для её решения следует записать формулу закона Архимеда:

F_ВЫТ = r_ЖgV_ТЕЛА. (2.16)

Здесь F_ВЫТ – выталкивающая сила, r_Ж – плотность жидкости (газа), V_ТЕЛА – объём части тела, погружённой в жидкость (газ).

· Если в задаче идёт речь о взаимодействующих точечных зарядах, следует записать формулу закона Кулона. Согласно этому закону:

– разноимённо заряженные тела притягиваются друг к другу, одноимённо заряженные – отталкиваются;

– сила взаимодействия тел прямо пропорциональна произведению их зарядов и обратно пропорциональна квадрату расстояния между ними;

– если тела – однородно заряженные шары, сферы или их можно считать точечными зарядами, справедлива формула (см. рис. 2.4)

F = 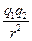. (2.17)

В формуле (2.17) e₀ = 8,85×10^-¹²Ф/м– электрическая постоянная, q₁ – заряд первого тела, q₂ – заряд второго тела (на рис. 2.4 знаки зарядов противоположные), r – расстояние между центрами тел (шаров, сфер), e – диэлектрическая проницаемость среды, в которой находятся тела, F – сила их электростатического взаимодействия.

Как мы отметим далее, если хотя бы одно из взаимодействующих заряженных тел – не точечное, не равномерно заряженные шарик или сфера, напрямую формулой закона Кулона пользоваться нельзя, следует выразить силу 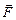, действующую на заряд q через напряженность электрического поля 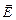, в котором находится заряд:

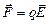. (2.18)

Типичная ситуация, описываемая этой формулой – поведение точечного заряда, шарика, покоящегося или движущегося в однородном электрическом поле.

· Если в задаче идёт речь о проводнике с током, находящемся в магнитном поле, следует записать формулу для силы Ампера:

F_А = BIlsina. (2.19)

Здесь B – индукция магнитного поля, в котором находится прямой проводник длиной l, по которому идёт ток I, a – угол между направлением протекания тока и направлением вектора . Направление вектора силы 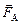, действующей на проводник с током, находится по правилу левой руки.

· Если в задаче идёт речь об электрическом заряде, движущемся в магнитном поле, для её решения следует записать формулу силы Лоренца:

F_Л = Bqusina. (2.20)

В этой формуле B – индукция магнитного поля, q – заряд, движущийся со скоростью u, a – угол между направлением скорости заряда и направлением вектора . Направление вектора силы 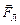, действующей на движущийся положительный заряд, находится по правилу левой руки. Если заряд – отрицательный, то найденное по правилу левой руки направление силы следует поменять на противоположное.

· Если в задаче идёт речь о теле, находящемся в состоянии покоя (или равномерного прямолинейного движения), следует записать:

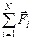= 0. (2.21)

Некоторые примеры

О массе

- Электрон – 9,1×10^-³¹ кг.

- Пуля автомата Калашникова – 7,4×10^-³ кг.

- Первый искусственный спутник Земли – 83,6 кг.

- Автомобиль «Волга» (ГАЗ-24) – 1,42×10³ кг.

- Слон – до 4,5×10³ кг.

- Трактор К-700 – 11×10³ кг.

- Четырёхосный железнодорожный грузовой вагон – 22,6×10³ кг.

- Цельнометаллический пассажирский вагон – 54×10³ кг.

- Самый большой из добытых китов – 150×10³ кг

- Электровоз ВЛ10 – 184×10³ кг.

- Обычная масса грузового поезда – до 24000×10³ кг.

- Масса самых тяжелых поездов, проведенных в порядке эксперимента, превышает 40000×10³ кг.

- Останкинская телевизионная башня – 55000×10³ кг.

О силе тяги

- Первый паровоз «Ракета» Стефенсона – до 2,8 кН.

- Трактор колёсный К-700 при скорости 2,6 км/ч – 60 кН.

- Двухсекционный тепловоз 2ТЭ10 при скорости 24 км/ч – 510 кН.

- Тепловоз ТЭ3 при скорости 20 км/ч – 400 кН, при трогании с места – 610 кН.

- Электровоз ВЛ80^к при скорости 51,6 км/ч – 460 кН.

- Электровоз ВЛ10 при скорости 47,3 км/ч – 390 кН.

- Суммарная тяга двигателей первой ступени ракеты-носителя корабля «Восток» – 5000 кН.

- Суммарная тяга двигателей ракеты-носителя «Энергия» в начале полёта – 353000 кН.

Вопросы для повторения

1. Что называется импульсом материальной точки? Импульсом системы материальных точек?

2. Что называется системой отсчёта? Что такое инерциальная система отсчёта? Приведите примеры.

3. Сформулируйте первый закон Ньютона, приведите примеры его проявления.

4. Сформулируйте второй закон Ньютона, приведите примеры его проявления.

5. Продемонстрируйте, в каком случае из формулы второго закона Ньютона, записанной в общем виде, можно получить упрощённое соотношение F = ma.

6. Сформулируйте третий закон Ньютона, приведите примеры его проявления.

7. Какие действия следует предпринять при решении задачи, если в ней встречается понятие «силы»?

8. Перечислите основные виды сил, встречающихся при решении стандартных задач по физике, и запишите соответствующие формулы.

Сформулируйте закон Всемирного тяготения. Ответ поясните рисунком.

<1 2 345 6 7 >

Дата добавления: 2020-02-05; просмотров: 571;