Лекция 2 МЕХАНИКА. ЧАСТЬ II

2.1 МАССА И ИМПУЛЬС ТЕЛА

2.1.1 Масса

2.1.2 Импульс

2.2 ДИНАМИКА. ЗАКОНЫ НЬЮТОНА

2.2.1 Понятие силы. Инерциальные системы отсчёта. Первый закон Ньютона

2.2.2 Второй закон Ньютона

2.2.3 Третий закон Ньютона. Вес тела

2.2.4 Закон Всемирного тяготения

2.2.5 Примеры сил. Рекомендации к решению стандартных задач по физике

Некоторые примеры

Вопросы для повторения

2.1 МАССА И ИМПУЛЬС ТЕЛА

2.1.1 Масса

Практика показывает, что при одном и том же воздействии разные тела приобретают неодинаковые скорости. Поместим на гладкую горизонтальную поверхность вблизи неподвижной стенки тело (брусок) А и установим между стенкой и телом сжатую пружину (рис. 2.1.а). Если пружину отпустить, первоначально покоившееся тело придёт в движение и в итоге приобретёт некоторую скорость u₁.

Прикрепим к бруску А ещё три таких же – рис. 2.1.б, вновь сожмём пружину (так же, как и в предыдущем случае) и затем отпустим её: после разлёта скорость u₂ системы из четырёх тел окажется вдвое меньше, чем у одного тела А. Система из девяти одинаковых скреплённых тел после распрямления пружины будет иметь в три раза меньшую скорость и т. д. Таким образом, данный эксперимент даёт возможность количественно описать инертные свойства системы, её способность ускоряться или замедляться в результате внешних воздействий. Мерой инертных свойств тела является его масса.

Пусть брусок А – эталонное тело, и ему соответствует эталонная масса m₁ = 1 (единицу измерения этого параметра в СИ называют килограммом). Тогда массу m любого другого тела можно определить, сравнив его скорость в условиях нашего эксперимента со скоростью эталона:

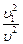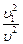= , или m = m₁ (кг).

За массу в 1 кг в своё время была выбрана масса 1 л дистиллированной воды, взятой при +4 °С (именно при этой температуре вода имеет максимальную плотность). Из платиново-иридиевого сплава была изготовлена гиря такой же массы, которая и считается эталоном одного килограмма. Гиря хранится в Парижской палате мер и весов (промышленно развитые страны имеют копии этого эталона).

2.1.2 Импульс

Импульсом материальной точки назовём вектор

= m 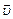, (2.1)

где m – масса материальной точки, 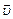– её скорость. Любое тело можно представить в виде системы – совокупности частей с массами m_i и скоростями каждая. В этом случае импульсом тела, состоящего из N частей, каждую из которых с хорошей точностью можно считать материальной точкой, назовём вектор

= = .

Аналогично, для системы тел:

= ,

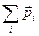где – импульс каждого отдельного тела.

Единица измерения импульса в СИ – кг×м×с^-1.

ВАЖНО: импульс является вектором, то есть за обозначением скрываются три скалярных величины (проекции импульса на выбираемые в условиях каждой конкретной задачи оси координат): p_X, p_Y и p_Z.

2.2 ДИНАМИКА. ЗАКОНЫ НЬЮТОНА

2.2.1 Понятие силы. Инерциальные системы отсчёта. Первый закон Ньютона

Если кинематика занимается описанием характера движения тела, не рассматривая причин возникновения и изменения этого движения, то центральной идеей динамики как раз и является учёт причин внешнего воздействия на тело. Для описания каждого воздействия вводится вектор соответствующей ему силы 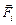, но поскольку воздействия могут быть совершенно разными, то единого определения (такого, как, например, для скорости, ускорения, импульса) вектору силы дать не удаётся.

Вообще говоря, в природе существуют только четыре вида фундаментальных взаимодействий, к которым сводятся все силы: гравитационное, электромагнитное, сильное и слабое. Последние два проявляются на уровне микромира; в обыденной жизни мы чаще всего имеем дело с первыми двумя, причём практически всё то, что мы обозначаем термином «сила» (силы реакция опоры, трения, упругости и многие другие), в итоге является следствием электромагнитного взаимодействия зарядов, входящих в состав атомов и молекул.

Об основных видах сил, с которыми мы встречаемся при решении практических задач, мы поговорим ниже.

Прежде, чем мы обсудим законы динамики Ньютона, следует дать ещё одно определение.

Системой отсчёта будем называть совокупность системы координат и устройства, отсчитывающего время (часов). Как мы уже отмечали на первой лекции, чаще всего на практике используется декартова прямоугольная система координат.

Первый закон Ньютона:существуют такие системы отсчёта, в которых тело движется равномерно прямолинейно или покоится до тех пор, пока внешние воздействия не выведут его из этого состояния.

Таким образом: а) вслед за Ньютоном мы постулируем наличие таких систем отсчёта, в которых выполняется закон, и б) мы делаем вывод о том, что в данной системе отсчёта тело будет двигаться равномерно прямолинейно или покоиться, если на него не действуют внешние силы.

В реальности, конечно, невозможно представить себе тело, на которое вообще никакие силы не действуют: на все объекты, например, действуют силы гравитационного притяжения со стороны других тел. Но поскольку сила является вектором, может оказаться, что сумма всех сил, действующих на тело со стороны других объектов, равна нулю ( 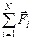= 0), и тогда, действительно, скорость тела будет постоянной (или даже равной нулю).

Системы отсчёта, в которых выполняется этот закон, называются инерциальными.

Таким образом, инерциальными являются любые системы отсчёта, которые покоятся друг относительно друга, или одна из них движется относительно другой равномерно прямолинейно.

Следует помнить, что равномерное прямолинейное движение в природе встречается достаточно редко и длится недолго. Так, например, с домом у дороги и с проезжающим мимо него с заданной скоростью автомобилем можно связать инерциальные системы отсчёта, однако следует помнить, что поверхность Земли не является плоскостью, а, значит, организовать по её поверхности прямолинейное движение не так-то легко.

Сама Земля вращается как вокруг своей оси, так и вокруг Солнца, поэтому системы отсчёта, связанные с Солнцем и Землёй, вообще говоря, инерциальными считать тоже нельзя…

2.2.2 Второй закон Ньютона

Как правило, любое тело одновременно испытывает воздействие со стороны многих объектов, то есть на него действует не одна, а несколько сил. Согласно второму закону Ньютона сумма всех сил, действующих на тело, равна скорости изменения его импульса:

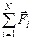= . (2.2)

Заметим, что сила – вектор, и суммирование в этой формуле должно производиться по правилам сложения векторов (по правилу параллелограмма или же по отдельности для каждой из проекций сил).

Формулировка закона ещё раз напоминает нам, что скоростью изменения какой-либо функции (в нашем случае – импульса) называется первая производная этой функции по времени.

Проанализируем выражение (2.2).

Сумму всех сил, действующих на тело, заменим одной результирующей силой:

= .

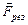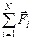Воспользовавшись определением импульса, распишем, чему равна скорость его изменения:

.

По определению ускорения – см. формулу (1.2):

, то есть .

Если масса тела не меняется в процессе его движения (m = const, или = 0), то формула (2.2) приобретает вид, хорошо известный из школьного курса физики:

. (2.3)

Таким образом, известное выражение (2.3) справедливо лишь для случая, когда масса тела, движущегося под действием некоторой постоянной силы 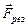, не меняется со временем.

Давайте ответим на вопрос, меняется ли в процессе движения

- масса грузовика? (Да? Нет?)

- масса самолёта? (Да? Нет?)

- масса стартующей ракеты? (Да? Нет?)

В последнем случае очевиден ответ – «Да», поскольку при взлете ракеты сжигаются десятки тонн горючего (да и ставшие пустыми баки разгонных ступеней сбрасываются). Но горючее сжигается и при полёте самолёта, и при движении грузовика! Просто соответствующим изменением массы мы зачастую пренебрегаем по сравнению с массой самого движущегося объекта: именно поэтому при решении школьных задач из раздела «динамика» мы привыкли использовать формулу второго закона Ньютона не в виде (2.2), а в виде (2.3).

Существует ещё одно важное соображение, которое необходимо иметь в виду, когда мы говорим, что именно формула (2.2), а не (2.3) является основной для второго закона.

Дело в том, что импульс тела с увеличением его скорости возрастает не прямо пропорционально u. Более общая по сравнению с классической механикой теория – специальная теория относительности – говорит о том, что на самом деле импульс тела связан с его скоростью соотношением

, (2.4)

где m₀ – масса покоящегося тела (масса покоя); с – скорость света в вакууме.

Дробь в формуле (3.5) часто интерпретируется, как масса m тела, движущегося со скоростью u:

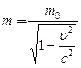, (2.5)

Сказанное означает, что по мере разгона тела его масса увеличивается. Особенно заметным это оказывается при достижении скоростей, близких к скорости света: при u << с (что как раз и имеет место в классической механике) подкоренное выражение в формулах (2.4) и (2.5) практически равно единице, и m » m₀. Однако, если всё же учесть возможность разгона тела до больших скоростей, то понятно, что формула второго закона Ньютона в виде (2.3) при этом перестанет работать, в то время как выражение (2.2) с учётом формулы (2.4) для импульса будет по-прежнему оставаться справедливым.

Для современных науки и техники процессы, в которых подтверждается справедливость релятивистских (от английского relatiuity – относительность) соотношений (2.4) и (2.5), стали уже вполне обыденными, не вызывает сомнений и корректность приведённой выше формулировки второго закона Ньютона. Тем удивительнее то, что Ньютон, живший за две с лишним сотни лет до создания СТО, сформулировал свой второй закон именно в виде (2.2)– общем, справедливом даже в релятивистской физике, а не в упрощённом (2.3), который применим только в физике классической (и то лишь, если m = const).

В заключение заметим, что формулы (2.2) и (2.3) позволяют определить единицу измерения силы. В СИ сила измеряется в ньютонах; 1 Н =1 кг×м/с².

2.2.3 Третий закон Ньютона. Вес тела