Лекция 3 МЕХАНИКА. ЧАСТЬ III

3.1 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

3.1.1 Центр масс системы материальных точек. Модель абсолютно твёрдого тела

3.1.2 Момент инерции. Теорема Штейнера

3.1.3 Момент импульса

3.1.4 Момент силы

3.1.5 Основной закон динамики вращательного движения.

Некоторые примеры

Вопросы для повторения

3.1 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

3.1.1 Центр масс системы материальных точек.

Модель абсолютно твёрдого тела

До сих пор мы рассматривали вопросы, связанные с кинематикой и динамикой объёктов, размерами которых пренебрегали по сравнению с другими расстояниями, характерными для конкретной задачи (путём, который проходит объект, расстоянием между взаимодействующими объектами и т. д.). Оказывается, что во многих случаях объёкт даже значительных размеров можно рассматривать как набор, совокупность достаточно малых частей, но при этом описывать движение лишь одной точки полученной системы – центра масс.

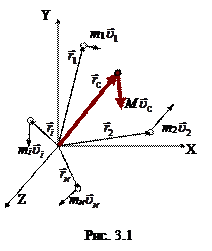
Пусть имеется система, состоящая из N материальных точек с массами m_i, каждая из которых в данный момент имеет свою скорость , а их положение задаётся радиус-векторами 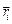(рис. 3.1). Центром масс системы назовём точку, положение которой определяется радиус-вектором 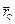таким, что:

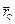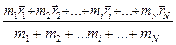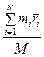= = , (3.1)

где M – суммарная масса системы точек. Продифференцировав правую и левую части формулы по времени и используя определение скорости, получаем выражение для скорости центра масс

= = ,

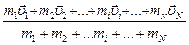и тогда для импульса системы 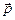= 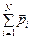можно записать:

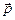= = M . (3.2)

Если на каждую точку системы будет действовать своя сила 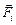, то для описания того, куда в итоге станет двигаться вся система в целом, не нужно писать N уравнений вида 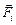= для каждой точки в отдельности. Достаточно записать одно подобное уравнение для центра масс, решив которое и использовав соответствующие уравнения кинематики, мы сможем предсказать, где окажется центр масс системы в заданный момент времени:

= = = = .

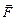В частности, если масса точек не меняется со временем, можно записать:

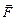= M ,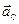

где 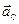– ускорение центра масс.

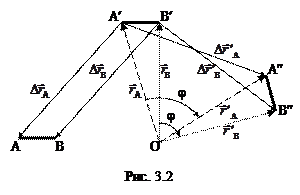
Если система точек, на которые мы мысленно разбиваем тело, движется так, что за равные промежутки времени вектора их перемещений оказываются одинаковыми (и по величине и по направлению), то такое движение тела называется поступательным. Пример: при переносе отрезка AB в положение A¢B¢ (рис. 3.2) вектора перемещения всех его точек равны (в частности, = ).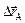

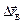Если все взаимные расстояния между точками тела не меняются со временем, такое тело будем называть абсолютно твёрдым.

Помимо поступательного движения точки абсолютно твёрдого тела могут испытывать вращательное движение, при котором оказывается одинаковым угол поворота радиус-векторов всех точек; вектора перемещения этих точек при этом не совпадают по направлению (на рис. 3.2 это перенос отрезка AB в положение A²B², при котором 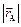= , 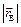= 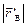, но ¹ ).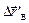

В общем случае движение твёрдого тела в каждый момент времени можно рассматривать как совокупность поступательного движения одной точки (центра масс) и его вращательного движения относительно некоторой мгновенно выбранной оси. Поскольку мы живём в мире, характеризующемся тремя измерениями, удобно рассматривать оба типа движения относительно взаимно перпендикулярных осей: трёх (X, Y и Z), связанных с точкой отсчёта (относительно неё центр масс движется поступательно) и трёх (X¢, Y¢ и Z¢), связанных с движущимся центром масс, относительно которых тело вращается (рис. 3.3). В итоге свободно движущееся твёрдое тело может иметь шесть степеней свободы: три поступательных с компонентами линейной скорости центра масс u_CX, u_CY и u_CZ, и три вращательных, с компонентами угловой скорости w_X¢, w_Y¢ и w_Z¢ относительно проходящих через него осей.

3.1.2 Момент инерции. Теорема Штейнера

Как мы уже говорили в разделе «кинематика», для упрощения математического описания вращательного движения удобно использовать характеристики, связанные не с линейным перемещением объёкта, а с угловым (углом поворота, угловой скоростью, угловым ускорением). При этом получаемые формулы по структуре оказываются подобны тем, которые выводятся в кинематике поступательного движения. Данный подход используется и в динамике вращательного движения, для описания которого можно ввести свои характеристики – аналоги ряда характеристик, используемых в динамике поступательного движения.

Прошлую лекцию мы начали с обсуждения понятия «масса» тела. Аналогом массы (мерой инертных свойств тела) при описании вращения является момент инерции.

Моментом инерции материальной точки относительно некоторой оси называется выражение вида

I = mr², (3.3)

где m – масса точки, r – расстояние до этой оси.

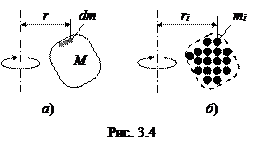
Момент инерции тела (которое можно представить в виде совокупности материальных точек – см. рис. 3.4.а), рассчитывается по формуле

I = , (3.4)

в которой знак интеграла означает суммирование моментов инерции всех точек с массами dm, из которых состоит тело массой M, причём каждая из них находится на своём расстоянии r от выбранной оси.

На практике тело удобно представлять в виде набора из N частей, каждую из которых с хорошей точностью можно считать точечной массой m_i, находящейся на расстоянии r_i от оси (рис. 3.4.б), и тогда момент инерции тела может быть рассчитан, как

I = 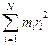. (3.5)

Из определения момента инерции следует, что его величина зависит не только от общей массы тела, но также и от формы тела и от распределения массы по его объёму (какие-то части тела, например, могут быть изготовлены из более тяжёлого материала, а какие-то – из более лёгкого).

Очевидно: момент инерции неодинаков относительно разных осей, и поэтому, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, например, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.

В некоторых случаях теоретический расчёт момента инерции достаточно прост. В качестве примера рассмотрим, как выводится выражение для I тонкого однородного кольца массой M и радиусом R относительно оси, проходящей через центр кольца перпендикулярно его плоскости (рис. 3.5).

Выделим на нашем кольце малый элемент массой dm. Поскольку он находится от оси вращение на расстоянии, равном радиусу кольца R, его момент инерции dI равен R²dm. Просуммировать моменты инерции всех элементов кольца означает взять интеграл вида I = . Учитывая, что для всех элементов расстояние R до оси вращения одинаково, множитель R² вынесем за знак интеграла, и, так как 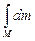= M, получим, что момент инерции кольца массой M и радиусом R относительно оси, проходящей через кольца перпендикулярно его плоскости

I = MR². (3.6)

Очевидно, что, поскольку толщина h кольца в итоговую формулу не входит, полученное выражение оказывается справедливым также для тонкого обруча и тонкостенного цилиндра.

Ось вращения может проходить через центр масс тела, а может и не проходить через него (рис. 3.6). В последнем случае для вычисления момента инерции пользуются теоремой Штейнера.

Согласно этой теореме, момент инерции тела I относительно произвольной оси равен сумме момента инерции I₀ относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела M на квадрат расстояния d между осями:

I = I₀ + Md². (3.7)

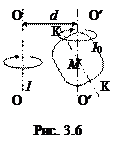На рис. 3.7 момент инерции I тела относительно вертикальной оси ОО равен моменту инерции I₀ относительно вертикальной же оси О¢О¢ плюс выражение Md². Существенно, что момент инерции I₀ определяется не относительно оси симметрии КК тела (иногда он бывает известен из теории), именно относительно оси О¢О¢, параллельной выбранной оси ОО.

В заключение в виде примеров приведём значения моментов инерции некоторых тел:

– момент инерции однородного диска (цилиндра) массой M и радиусом R относительно оси симметрии:

I = MR²;

– момент инерции однородного шара массой M и радиусом R относительно оси, проходящей через его центр:

I = 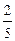MR²;

– момент инерции тонкого однородного стержня массой M и длиной l относительно оси, проходящей через его центр перпендикулярно самому стержню:

I = 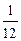Ml².

В общем случае момент инерции твёрдого тела I = kML², где M – его масса, L – некоторый геометрический параметр, k – коэффициент, зависящий от формы тела и его положения относительно интересующей нас оси. Заметим: от размеров тела R может зависеть и его масса. Так, моменты инерции двух изготовленных из одного материала однородных шаров, радиус одного из которых в два раза больше радиуса другого, будут отличаться не в четыре, как это могло бы показаться на первый взгляд, а в целых 32 раза! Это вызвано тем, что возрастание радиуса в два раза означает восьмикратное увеличение массы шара (объём V = 4/3×pR³, M = rV, где r – плотность материала шаров).

В СИ единицей измерения момента инерции является кг×м².

3.1.3 Момент импульса

Аналогом импульса 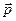материальной точки при описании вращательного движения является момент импульса 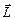. Момент импульса – это вектор, который имеет смысл только относительно выбранной точки (например, – связанной с началом отсчёта на осях координат). При этом так же, как и любой другой вектор, момент импульса можно представить в виде набора из трёх проекций на оси X, Y и Z. В этом случае говорят о моменте импульса относительно оси (L_Z, например), который, как и любая проекция, является уже скалярной величиной.

По определению моментом импульса материальной точки А, имеющей импульс 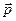, относительно некоторой точки О называется векторное произведение радиуса-вектора , проведённого из О в А, на импульс :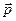

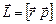(3.8)

Напомним, что, согласно определению векторного произведения, по величине L = rp×sina (здесь a – угол между векторами и 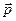); направление 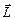определяется по правилу левой руки (или по правилу буравчика), см. рис. 3.7.

Моментом импульса системы точек (в том числе – тела) называется сумма моментов импульса всех точек, из которых эта система (тело) состоит.

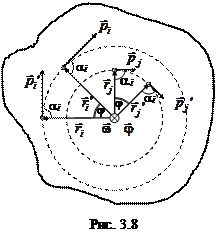Рассмотрим твёрдое тело, вращающееся вокруг некоторой оси, проходящей через его центр масс (рис. 3.8). При равномерном вращении за одно и то же время все точки тела поворачиваются относительно этой оси на один и тот же угол 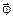, то есть они имеют одинаковую угловую скорость 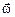. Кроме того, поскольку вектора линейных скоростей (а, следовательно, и импульсов 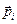) всех точек, из которых оно состоит, лежат в плоскостях, перпендикулярных оси вращения и (как при любом движении по окружности) одновременно перпендикулярны радиус-векторам 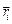, соединяющим ось с этими точками, все углы a_i между соответствующими векторам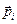и и 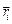оказываются равными 90º. Это означает, что для проекции момента импульса любой точки под номером i на ось вращения можно записать:

L_i = r_i p_i×sina_i = r_i p_i = r_im_iu_i =m_ir_i² = m_ir_i²w_i = m_ir_i²w.

Для проекции момента импульса всего тела на ось вращения:

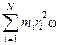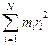L = = = = w = wI,

где I – момент инерции данного тела относительно этой же оси.

Таким образом, по аналогии с поступательным движением, которое характеризуется вектором импульса 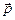(его проекции p_X, p_Y и p_Z, на оси координат: p_X = Mu_X, p_Y = Mu_Y, p_Z = Mu_Z), для описания вращательного движения абсолютно твёрдого тела вводится вектор момента импульса 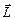. Проекции этого вектора L_X, L_Y и L_Z на оси координат равны, соответственно:

L_X = I_Xw_X, L_Y = I_Yw_Y, L_Z = I_Zw_Z.

Для момента импульса 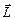симметричного твёрдого тела, вращающегося с угловой скоростью 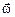, вокруг оси симметрии (относительно которой его момент инерции равен I), можно записать:

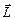= I 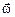. (3.9)

Из формулы следует, что в этом случае направление момента импульса абсолютно твёрдого тела совпадает с направлением вектора его угловой скорости.

Единица измерения момента импульса в СИ – кг×м²×с^-1.

3.1.4 Момент силы

Для описания внешних воздействий на объект при вращательном движении удобно использовать понятие момента силы.

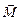Моментом силы относительно некоторой точки О называется векторное произведение радиуса-вектора , проведённого из О в точку приложения силы на саму силу :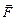

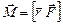. (3.10)

По величине M = rF×sina, где a – угол между векторами и 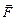. Направление вектора 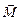определяется по правилу левой руки (или по правилу буравчика), рис. 3.9.

Можно также говорить о проекции момента сил M_Z на ось вращения Z. Данная проекция – скаляр и направления не имеет.

Произведение d = r×sina равно кратчайшему расстоянию от оси вращения до линии действия силы называется плечом силы. Поэтому можно записать:

M_Z = F d. (3.11)

Единица измерения момента силы в СИ – Н×м (ньютон-метр).

Согласно первому и второму законам Ньютона для того, чтобы тело находилось в состоянии покоя, для сил, действующих на тело, должно выполняться условие: 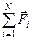= 0. Аналогичным образом, для того, чтобы тело находилось в состоянии равновесия, требуется, чтобы сумма моментов всех сил, действующих на тело, равнялась нулю:

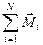= 0. (3.12)

В этой формуле речь идёт о векторной сумме моментов сил; если же найти проекции этих моментов на некоторую ось (в качестве которой удобно выбрать ось возможного вращения тела), то подобную формулу можно записать для алгебраической суммы моментов сил относительно этой оси:

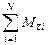= 0. (3.13)

Моментам сил, стремящихся повернуть тело относительно оси по часовой стрелке, обычно приписывают знак «плюс», против часовой стрелки – знак «минус» (пример мы рассмотрим ниже).

С понятием момента силы связано определение центра тяжести тела – точки, которая, вообще говоря, не совпадает с его центром масс.

Центром тяжести тела называется точка, относительно которой сумма моментов сил тяжести всех частей, на которые можно мысленно разбить тело, равна нулю.

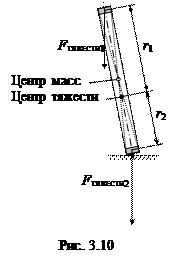
Если тело достаточно велико (например – это высокая башня цилиндрической формы, рис. 3.10), то её центр масс находится в геометрическом центре цилиндра. В то же время, вершина башни притягивается к Земле слабее, чем основание, поскольку, согласно закону Всемирного тяготения,

g = = = ,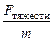

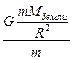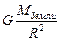то есть величина ускорения свободного падения зависит от расстояния до центра Земли (а вершина башни отстоит от центра Земли дальше, чем её основание). Поэтому центр тяжести такого объекта находится ниже его центра масс, для которого должно выполняться условие равенства моментов сил тяжести верхней и нижней частей. Используя обозначения, представленные на рисунке и учитывая, что относительно оси, проходящей через центр тяжести перпендикулярно плоскости рисунка, момент силы F_{ТЯЖЕСТИ1} стремится повернуть башню против часовой стрелки, а момент силы F_{ТЯЖЕСТИ2} – по часовой стрелке, можно сказать, что

F_{ТЯЖЕСТИ2}×r₂ - F_{ТЯЖЕСТИ1}×r₁ = 0.

Но, как мы отметили выше, F_{ТЯЖЕСТИ1} < F_{ТЯЖЕСТИ2}, следовательно, действительно: для выполнения данного равенства требуется, чтобы соблюдалось условие: r₁ > r₂.

Если изменением ускорения свободного падения при переходе от одной части тела к другой можно пренебречь (например, если размеры тела много меньше размеров планеты), то тогда можно считать, что центр тяжести тела совпадает с его центром масс.

3.1.5 Основной закон динамики вращательного движения

Основной закон динамики вращательного движения является аналогом второго закона Ньютона. Согласно этому законусумма моментов всех сил, действующих на тело, равна скорости изменения его момента импульса:

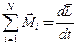. (3.14)

Если тело – абсолютно твёрдое, и вращается относительно закреплённой оси (относительно которой его момент инерции равен I), то эта формула приводится к виду:

,

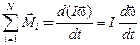а с учётом того, что, по определению, 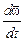= 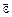, где 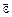– угловое ускорение, можно записать:

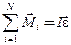, (3.15)

или

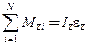(3.16)

(предполагается, что ось вращения обозначена как ось Z).

Порядок работы с этой формулой сходен с тем, который используется при решении задач на второй закон Ньютона: изображаем все силы, действующие на тело, выбираем ось вращения, находим проекции моментов сил на эту ось и записываем основной закон динамики вращательного движения для проекций (с учётом их знаков).

Некоторые примеры

- Момент инерции Земли относительно оси вращения в приближении её однородным сплошным шаром – 9,7×10³⁷ кг×м².

- Реальный момент инерции Земли относительно своей оси вращения – 8,0×10³⁷ кг×м².

- Момент инерции лунного модуля корабля «Аполлон» при половинном запасе топлива относительно осей, проходящих через его центр масс – около 33000 кг×м².

- Момент импульса Земли относительно своей оси вращения – около 4,2×10²⁹ кг×м×с^-1.

- Момент импульса Земли относительно центра Солнца (в приближении орбиты окружностью радиусом 1 а. е.) – около 2,7×10⁴⁰ кг×м×с^-1.

- Собственный (спиновый) момент импульса электрона – примерно 0,9×10^-34 кг×м×с^-1.

- Максимальный момент силы, прикладываемый к ключу дверного замка при его открывании и закрывании не должен превышать 0,6 Н×м (ГОСТ 23306-87).

- Для разрушения большой берцовой кости взрослого человека момент скручивающей силы должен превысить 30 – 140 Н×м.

- Крутящий момент силы затягивания свечей зажигания двигателя автомобиля 10 – 40 Н×м.

- Крутящий момент силы двигателя автомобиля Audi Q7 – до 500 Н×м (при 2750 об/мин).

- Крутящий момент силы на выходе зубчатой передачи серии PM (Renold plc) – до 12000 Н×м.

Вопросы для повторения

1. Что называется моментом инерции а) материальной точки, б) системы материальных точек, в) тела? Ответ поясните рисунками.

2. Сформулируйте теорему Штейнера. Ответ поясните рисунком.

3. Что называется моментом импульса малого объекта относительно некоторой точки? Ответ поясните рисунком.

4. Что называется моментом импульса малого объекта относительно некоторой оси? Ответ поясните рисунком.

5. . Что называется моментом силы относительно некоторой точки? Ответ поясните рисунком.

6. Что называется моментом силы относительно некоторой оси? Ответ поясните рисунком.

7. Какие точки называются а) центром масс тела, б) центром тяжести тела? В каком случае они совпадают?

8. Сформулируйте основной закон динамики вращательного движения и запишите соответствующие формулы а) в случае системы точек, б) в случае абсолютно твёрдого тела.

9. Какое тело называется абсолютно твёрдым?

Приведите примеры параметров-аналогов и законов-аналогов в динамике поступательного и вращательного движения.