Лекция 5 МЕХАНИКА. ЧАСТЬ V
5.1 РАБОТА И ЭНЕРГИЯ (ОКОНЧАНИЕ)
5.1.1 Потенциальная энергия
5.2 ЗАКОНЫ СОХРАНЕНИЯ
5.2.1 Закон сохранения импульса
5.2.2 Закон сохранения момента импульса. Трёхстепенной гироскоп
5.2.3 Закон сохранения механической энергии
5.2.4 О законах сохранения в природе. Принцип симметрии
Некоторые примеры
Вопросы для повторения
5.1 РАБОТА И ЭНЕРГИЯ (ОКОНЧАНИЕ)
5.1.1 Потенциальная энергия
Рассмотрим два примера вывода формул для расчёта потенциальной энергии.
Пример 1. Потенциальная энергия тела в поле сил тяжести
 При перемещении тела из точки 1 в точку 2 (расположенную на поверхности Земли, рис. 5.1) по отрезку 1-2 сила тяжести совершает работу A =
При перемещении тела из точки 1 в точку 2 (расположенную на поверхности Земли, рис. 5.1) по отрезку 1-2 сила тяжести совершает работу A = 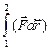 . Если высота, на которой находилось тело в начале траектории, не слишком большая, то изменением с высотой ускорения свободного падения g можно пренебречь, и тогда, согласно рисунку,
. Если высота, на которой находилось тело в начале траектории, не слишком большая, то изменением с высотой ускорения свободного падения g можно пренебречь, и тогда, согласно рисунку,
A =  =
= 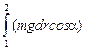 =
=
= mg×cosa  = mgl×cosa = mgh.
= mgl×cosa = mgh.
Но по определению A = WП1 - WП2, и, полагая, что на поверхности Земли (в точке 2) WП2 = 0, получаем, что A = WП1. Таким образом, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли (в предположении, что g не меняется с высотой), рассчитывается по формуле
WП = mgh. (5.1)
Пример 2. Потенциальная энергия упруго деформированной пружины
Рассмотрим тело, закреплённое на упруго деформированной (например, – растянутой) пружине жёсткостью k.
 |
Мы знаем, что если тело сместить от положения равновесия на расстояние x, на него со стороны пружины будет действовать сила FУПР, по величине равная kïxï, стремящаяся вернуть тело в положение равновесия, в котором x = 0 (рис. 5.2).
В процессе возврата тела в такое положение (из точки с координатой x в точку с координатой 0) упругая сила совершит работу:
A =  =
=  = -k
= -k  = -
= - 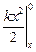 =
= 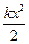 .
.
В положении равновесия потенциальную энергию пружины примем равной нулю, тогда вновь, согласно определению, можно записать A = WП1 - WП2 = WП1, то есть потенциальная энергия упруго деформированной пружины описывается формулой
WП = 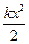 . (5. 2)
. (5. 2)
Заметим: в ходе вывода формулы мы ещё раз (как и в случае вычисления второй космической скорости) продемонстрировали, как рассчитывается работа переменной силы. Подобную же процедуру мы проделаем позднее (в разделе «Электростатика») при получении формулы для расчёта потенциальной энергии одного точечного заряда в поле другого точечного заряда.
5.2 ЗАКОНЫ СОХРАНЕНИЯ
Среди законов природы, известных человечеству, выделяется группа, имеющая всеобщий характер, и непосредственно отражающая фундаментальные свойства нашей Вселенной. Это – законы сохранения. Обсудим основные из их.
5.2.1 Закон сохранения импульса
Начнём с определения.
Пусть имеется система, состоящая из N материальных точек (или тел), импульсы которых обозначим: 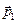 ,
,  ,…,
,…, 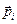 , …,
, …, 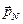 (напоминаем, что импульсом материальной точки, имеющей массу mi и скорость
(напоминаем, что импульсом материальной точки, имеющей массу mi и скорость  , называется произведение
, называется произведение 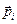 = mi
= mi  ). Система называется замкнутой, если на неё не действуют внешние силы (или такие силы действуют, но их сумма равна нулю).
). Система называется замкнутой, если на неё не действуют внешние силы (или такие силы действуют, но их сумма равна нулю).
Оказывается, что для такой системы всегда выполняется закон сохранения импульса: суммарный импульс замкнутой системы материальных точек (тел) не меняется со временем:
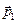 +
+  +… +
+… + 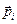 + … +
+ … + 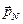 = const. (5.3)
= const. (5.3)
Заметим: импульс – вектор, и складывать импульсы необходимо соответствующим образом: либо по правилу параллелограмма, либо – складывая проекции этих векторов.
Типичным примером проявления закона сохранения импульса является реактивное движение. Пока ракета покоится, её импульс равен нулю; в результате сгорания топлива вырвавшаяся из сопла со скоростью u1 порция газов массой m движется в одну строну, а сама ракета, имеющая массу M, – со скоростью u2 в противоположную сторону так, с что суммарный импульс системы остаётся нулевым (Mu2 - mu1 = 0). Правда, по мере сгорания топлива масса ракеты непрерывно уменьшается, а скорость потока газа относительно Земли становится всё меньше, и это необходимо учитывать при выводе уравнения реактивного движения.
Можно задать себе вопрос: а что происходит с системой тел в случае, если она незамкнута? Ответ даёт второй закон Ньютона: если на систему в течение некоторого времениDtдействуют силы, равнодействующая которых равна 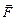 , то импульс
, то импульс 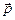 системы меняется на
системы меняется на 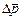
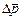 =
= 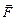 Dt (5.4)
Dt (5.4)
и становится равным 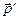 =
= 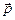 +
+ 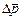 (здесь сложение – векторное).
(здесь сложение – векторное).
5.2.2 Закон сохранения момента импульса. Трёхстепенной гироскоп
Напомним, что моментом импульса 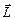 малого объекта, имеющего импульс
малого объекта, имеющего импульс 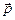 , относительно некоторой точки, расстояние от которой до объекта задаётся радиус-вектором
, относительно некоторой точки, расстояние от которой до объекта задаётся радиус-вектором  , называется векторное произведение
, называется векторное произведение 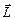 = [
= [  ,
, 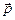 ].
].
Введём определение.
Пусть имеется система N материальных точек, импульсы которых обозначим 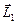 ,
,  , …,
, …,  , … ,
, … ,  . Будем называть эту систему замкнутой, если на неё не действуют внешние моменты сил (или действуют, но их сумма равна нулю).
. Будем называть эту систему замкнутой, если на неё не действуют внешние моменты сил (или действуют, но их сумма равна нулю).
Закон сохранения момента импульса: суммарный момент импульса замкнутой системы материальных точек (тел) не меняется со временем:
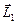 +
+  +…+
+…+  +…+
+…+  = const. (5.5)
= const. (5.5)
Момент импульса – вектор, направленный вдоль оси, вокруг которой движется тело (или оси вращения самого тела), а это означает, что так же, как и в случае закона сохранения импульса 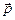 , складывать моменты импульсов необходимо либо по правилу параллелограмма, либо – суммируя проекции этих векторов.
, складывать моменты импульсов необходимо либо по правилу параллелограмма, либо – суммируя проекции этих векторов.
Замечание: Пусть момент инерции тела I относительно некоторой закреплённой оси вращения не меняется со временем, тогда, как мы показали ранее, с учётом того, что угловая скорость вращения 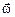 всех его точек (естественно, кроме тех, которые лежат на самой оси вращения – они не движутся) одинакова, можно записать:
всех его точек (естественно, кроме тех, которые лежат на самой оси вращения – они не движутся) одинакова, можно записать: 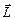 = I
= I 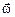 . Если же момент инерции тела изменится под действием внутренних сил, то, согласно закону сохранения момента импульса, поменяется по величине и его угловая скорость: I1
. Если же момент инерции тела изменится под действием внутренних сил, то, согласно закону сохранения момента импульса, поменяется по величине и его угловая скорость: I1 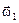 = I2
= I2  , и, следовательно,
, и, следовательно,
 =
= 
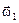 . (5.6)
. (5.6)
Приведём два примера такой ситуации.
- Если фигурист, быстро вращающийся на льду с прижатыми к груди руками, вдруг резко разведёт их в стороны (и тем самым увеличит свой момент инерции), то скорость его вращения уменьшится.
- Если звезда в процессе своей эволюции начинает сжиматься (то есть, её момент инерции будет уменьшаться), скорость вращения звезды возрастает. Во Вселенной это явление наблюдается при коллапсе звёзд из состояния белого карлика в нейтронную звезду. Процесс может носить взрывной характер и сопровождаться выделением громадной энергии: земным наблюдателем этот взрыв воспринимается как вспышка сверхновой.
Разберём ещё один пример, связанный с использованием закона сохранения момента импульса в технике: рассмотрим принцип работы трёхстепенного гироскопа.
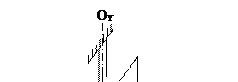 Как мы говорили на прошлой лекции, гироскопом называется массивное твёрдое тело, вращающееся с большой скоростью вокруг одной из своих осей симметрии. Трёхстепенной гироскоп располагается в подвесе, позволяющем ему свободно поворачиваться не только относительно этой оси, но и еще относительно двух других, перпендикулярных друг другу и первой оси, при этом точка пересечения всех трёх осей должна совпадать с центром тяжести гироскопа. Такой подвес называется кардановым (по имени по имени Д. Кардано, (1501 – 1576), который, кстати, не изобретал его, а лишь описал в своей книге «Хитроумное устройство вещей», получившей в своё время широкую известность). Главным свойством карданова подвеса является то, что если в него закрепить вращающееся тело, то оно будет сохранять направление оси вращения независимо от ориентации самого подвеса.
Как мы говорили на прошлой лекции, гироскопом называется массивное твёрдое тело, вращающееся с большой скоростью вокруг одной из своих осей симметрии. Трёхстепенной гироскоп располагается в подвесе, позволяющем ему свободно поворачиваться не только относительно этой оси, но и еще относительно двух других, перпендикулярных друг другу и первой оси, при этом точка пересечения всех трёх осей должна совпадать с центром тяжести гироскопа. Такой подвес называется кардановым (по имени по имени Д. Кардано, (1501 – 1576), который, кстати, не изобретал его, а лишь описал в своей книге «Хитроумное устройство вещей», получившей в своё время широкую известность). Главным свойством карданова подвеса является то, что если в него закрепить вращающееся тело, то оно будет сохранять направление оси вращения независимо от ориентации самого подвеса.
Рассмотрим работу трёхстепенного гироскопа (рис. 5.3) подробнее.
На гироскоп (массивный цилиндр), вращающийся с большой скоростью относительно оси OXO¢X, и имеющий момент импульса 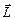 действуют сила тяжести
действуют сила тяжести  , силы реакции опоры
, силы реакции опоры  и
и 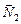 в подшипниках на оси вращения и (возможно) силы трения в самих подшипниках. Однако, момент силы тяжести равен нулю относительно любой их трёх осей OXO¢X, OYO¢Y и OZO¢Z (так как равно нулю расстояние от точки приложения силы тяжести до любой из этих осей). Моменты сил
в подшипниках на оси вращения и (возможно) силы трения в самих подшипниках. Однако, момент силы тяжести равен нулю относительно любой их трёх осей OXO¢X, OYO¢Y и OZO¢Z (так как равно нулю расстояние от точки приложения силы тяжести до любой из этих осей). Моменты сил  и
и 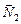 компенсируют друг друга (в силу симметрии устройства эти силы равны по величине и приложены на одинаковых расстояниях от любой из осей). Если использовать хорошие подшипники (например, подвеска – магнитная), то моментом сил трения всех трёх пар подшипников можно пренебречь. Сказанное означает, что сумма моментов всех сил, действующих на гироскоп, равна нулю, и, вследствие закона сохранения момента импульса, у раскрученного гироскопа величина и направление
компенсируют друг друга (в силу симметрии устройства эти силы равны по величине и приложены на одинаковых расстояниях от любой из осей). Если использовать хорошие подшипники (например, подвеска – магнитная), то моментом сил трения всех трёх пар подшипников можно пренебречь. Сказанное означает, что сумма моментов всех сил, действующих на гироскоп, равна нулю, и, вследствие закона сохранения момента импульса, у раскрученного гироскопа величина и направление 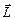 должны сохраняться неизменными. Приложение добавочных сил к опорам на оси OYO¢Y ситуации не меняют: моменты возникающих при этом сил в силу симметрии системы также одинаковы по величине и противоположны по направлению, то есть взаимно уничтожаются.
должны сохраняться неизменными. Приложение добавочных сил к опорам на оси OYO¢Y ситуации не меняют: моменты возникающих при этом сил в силу симметрии системы также одинаковы по величине и противоположны по направлению, то есть взаимно уничтожаются.
Тот факт, что ось трёхстепенного гироскопа сохраняет ориентацию в пространстве, позволяет использовать это устройство для создания компасов, не связанных с магнитным полем Земли (например – в космических аппаратах), транспортных средств, при любых вибрациях сохраняющих вертикальное положение, робототехнических системах, отслеживающих движение манипуляторов в пространстве и т. д.
Вот как, например, работает гироскоп в системе наведения баллистической ракеты: ось раскрученного гироскопа управляет движением полозка на реохорде, включённом в цепь поворота рулей ракеты. На определённой минуте полёта программа выдаёт задание на начало разворота, ракета вместе с реохордом поворачивается, но ось-то гироскопа (и связанный с ней движок реохорда) сохраняет ориентацию в пространстве! В результате поворота ракеты и смещения корпуса реохорда относительно оси гироскопа увеличивается длина одного из плеч, меняется его сопротивление. Поворот продолжается до тех пор, пока сопротивление не достигнет заданного программой полёта значения, после чего подаётся сигнал на прекращение поворота. Рули возвращаются в исходное положение, и ракета летит дальше с новым постоянным положением движка реохорда относительно его корпуса.
В настоящее время в некоторых странах (США, Японии) начато производство электрических компактных транспортных средств типа одно- и двухколёсных самокатов. Человек стоит на небольшой площадке или сидит в седле и только осуществляет управление: от падения его предохраняет гироскопическая система, обеспечивающая вертикальность устройства. Таким образом, трёхстепенные гироскопы уже давно перестали быть экзотикой и широко используются в разных видах транспорта.
В заключение данного параграфа ещё раз заметим: закон сохранения момента импульса выполняется только для замкнутой системы тел. Если же система незамкнута, её момент импульса меняется, причём, согласно основному закону динамики вращательного движения, изменение момента импульса 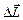 системы прямо пропорционально времени Dt действия момента
системы прямо пропорционально времени Dt действия момента 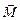 внешних сил:
внешних сил:
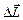 =
= 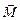 Dt (5.7)
Dt (5.7)
(см., например, явление прецессии).
5.2.3 Закон сохранения механической энергии
Как мы уже говорили, в механике полная энергия тела (или системы тел, материальных точек) складывается из его кинетической и потенциальной энергии. Закон сохранения энергии в механике: полная энергия замкнутой системы, в которой действуют лишь консервативные силы, не меняется со временем:
WК + WП = const. (5.8)
Сделаем несколько замечаний.
- В общем случае в выражение для полной механической энергии входит кинетическая энергия не только поступательного, но и вращательного движения.
- Если в системе присутствует сила трения, то полная энергия системы будет уменьшаться. Мы-то знаем, что энергия никуда не исчезнет: вследствие трения температура системы повысится, и энергия из механической перейдёт в тепловую. Однако, механика не оперирует с понятием «теплота», мы же должны описать, что происходит при этом именно в терминах механики. Аналогичная проблема возникает и в ситуации, когда система незамкнута, то есть на неё действует внешняя сила (силы): как выразить, что происходит с системой в этом случае? Ответ на этот вопрос таков:
Если система незамкнута и (или) в ней действуют неконсервативные силы, то изменение её полной механической энергии равно работе этих сил:
(WК2 + WП2 ) - (WК1 + WП1) = А. (5.9)
В этой формулеWК1, WК2 и WП1, WП2 – начальные и конечные значения, соответственно, потенциальной и кинетической энергии всех тел системы, А – работа внешних и (или) внутренних неконсервативных) сил.
Помимо потенциальной и кинетической бывают другие виды энергии, например, внутренняя, связанная с тепловым движением атомов и молекул, из которых состоит тело. Распространение понятия энергия на другие области физики (где также действуют силы, способные совершать работу) привело в итоге к открытию общего закона сохранения энергии:
Дата добавления: 2020-02-05; просмотров: 750;











