Лекция 4 МЕХАНИКА. ЧАСТЬ IV

4.1 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ (пример)

4.1. Прецессия гироскопа

4.2 РАБОТА И ЭНЕРГИЯ

4.2.1 Работа силы. Мощность

4.2.2 Кинетическая энергия

4.2.3 Первая и вторая космические скорости

4.2.4 Потенциальная энергия (определения)

Некоторые примеры

Вопросы для повторения

4.1 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ (пример)

4.1 Прецессия гироскопа

В качестве примера проявления основного закона динамики вращательного движения объясним явление прецессии гироскопа.

Гироскопом называется симметричный объект, вращающийся с большой скоростью относительно одной из своих осей симметрии. Если на такой объект действует сила, создающая момент который стремится повернуть ось вращения, возникает явление прецессии – ось вращения начинает описывать в пространстве конусообразную поверхность, ось симметрии которой совпадает с направлением действия силы. Примером прецессии является движение вращающегося волчка, ось которого выведена из вертикального положения; ещё один пример – прецессия электронных орбит в атоме, которую мы рассмотрим позднее при объяснении явления диамагнетизма.

На рис. 4.1.а) изображено положение вращающегося волчка в некоторый момент времени. Ось вращения ОО¢ наклонена относительно вертикали на некоторый угол, волчок вращается так, что вектор его угловой скорости (и, соответственно, вектор момента импульса 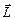) в этот момент находятся в плоскости рисунка.

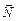На гироскоп действуют две силы, приложенные в разных точках: сила тяжести и сила реакции опоры . Если бы гироскоп не вращался, он бы упал, поворачиваясь в плоскости рисунка по часовой стрелке относительно оси, проходящей через точку О перпендикулярно этой плоскости. Падение обусловлено действием момента силы тяжести относительно точки О (он направлен вглубь рисунка); момент силы реакции опоры 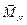относительно этой точки равен нулю (нулю равно расстояние от точки О до точки приложения силы 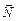). Поэтому основной закон динамики вращательного движения для гироскопа можно записать в виде:

= + = .

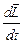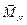Из данной формулы следует, что под действием момента силы тяжести у гироскопа за малое время dt появляется добавка к уже имевшемуся моменту импульса 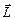– тоже малая и направленная перпендикулярно ему (как и , – вглубь плоскости рисунка). В результате вектор 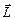переходит в вектор – тот же, что и 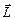по величине, но имеющий уже несколько иное направление (см. рис. 4.1.б), который является видом сверху схемы расположения векторов , 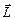и при прецессии). Это означает, что и ось вращения гироскопа вместе с ним самим теперь уже не лежит в плоскости рисунка!

Изменение положения оси влечёт за собой изменение направления действия момента силы тяжести, который также «поворачивается» (теперь это ). Под его действием возникает новая добавка к моменту импульса, , которая, в свою очередь меняет направление вектора на , ось гироскопа продолжает движение, момент силы тяжести вновь меняет направление и т. д. Как результат, начинается прецессия – движение оси вращения гироскопа по конусообразной поверхности[3] относительно вертикальной оси (рис. 4.1.а). Примером прецессии является движение оси вращения закрученного волчка (юлы), в случае отклонения её от вертикали.

4.2 РАБОТА И ЭНЕРГИЯ

4.2.1 Работа силы. Мощность

Хотя использование второго закона Ньютона и позволяет найти ускорение тела и, тем самым, обеспечить решение задач кинематики, применить этот закон удаётся не всегда, особенно, если трудно сказать: все ли силы, действующие на тело, учтены, или если эти силы в процессе движения тела меняются. В таких случаях можно попытаться решить задачу описания движения тела, используя понятия работы и энергии.

Пусть тело совершает малое перемещение на 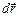, и при этом на него действует некая сила 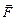. Тогда работой этой силы dA называется скалярное произведение векторов 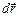и 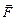, то есть выражение вида

dA = ( 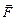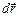) = F×dr×cosa, (4.1)

где a – угол между векторам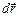и и .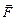

При движении тела по произвольной траектории от точки 1 к точке 2 угол a (и, вообще говоря, сама сила 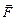) могут меняться, тогда работа этой силы будет равна сумме работ на малых участках, на которых и угол a и саму силу 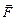можно считать практически неизменными:

A = 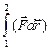. (4.2)

Если 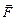не меняется со временем, а само тело движется по прямой (это означает, что a = const, а длина вектора его перемещения 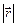равна пройденному пути S), то из (4.2) следует известное выражение для работы постоянной силы:

(3.3)

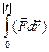А = = = F×cosa ,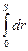

то есть

А = FScosa. (4.3)

Пример. Пусть тело поднимают вверх по наклонной плоскости (рис. 4.2). Помимо силы тяги 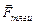, направленной под произвольным углом b к поверхности наклонной плоскости, на тело действуют сила тяжести , сила трения 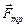и сила реакции опоры 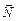. Если j– угол при основании наклонной плоскости, а S – путь, который проходит тело, то выражения для работы, совершаемой каждой из этих сил, можно записать следующим образом:

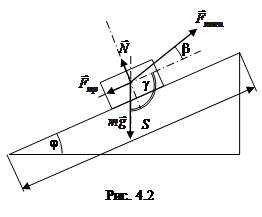
– работа силы тяжести A_mg = mgScosg = mgScos = -mgS×sina,

– работа силы реакции опорыA_N = NScos 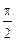= 0,

– работа силы трения A_тр = F_тр Scosp = -F_тр S,

– работа силы тяги A_тяги = F_тягиScosb.

Таким образом, может оказаться, что тело проходит некоторое расстояние, на всём пути на него действует сила, но работа этой силы равна нулю, поскольку угол между направлением действия силы и направлением вектора перемещения в каждый момент времени равен 90°. Примеры: работа силы реакции опоры на рис. 4.2, работа силы гравитационного притяжения к Земле спутника, летящего по круговой орбите, работа силы кулоновского притяжения электрона к ядру атома, работа силы Лоренца и т. д.

Работа, совершаемая постоянным моментом сил M при повороте тела на угол j:

А = M×j. (4.4)

В СИ работа измеряется в джоулях; 1 Дж = 1 Н×м.

С понятием работы тесно связано понятие мощности.

Средней мощностью N, развиваемой некоторым устройством, называется отношение производимой этим устройством работы Aко времени Dt, в течение которого эта работа совершается:

N= . (4.5)

Мгновенную мощность рассчитывают по формуле

N=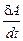

(здесь dA – работа, совершаемая за бесконечно малое время dt).

Если работу совершает двигатель автомобиля так, что при постоянной силе тяги F он движется с постоянной скоростью u, то мощность двигателя можно рассчитать следующим образом:

N = = = 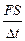F 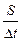= F u. (4.6)

Если работа совершается моментом сил по повороту тела на угол Dj с постоянной угловой скоростью w, развиваемая при этом мощность

N = = = Mw. (4.7)

В СИ мощность измеряется в ваттах, 1 Вт =1 Дж×с^-1.

Внесистемная единица работы (энергии): киловатт-час,

1 кВт×ч = 3,6×10⁶ Дж.

Внесистемная единица мощности: лошадиная сила,

1 л. с. » 735,5 Вт.

4.2.2 Кинетическая энергия

Работа является мерой изменения энергии тела или системы тел. В механике рассматриваются два вида энергии: кинетическая и потенциальная.

По определению кинетическая энергия при поступательном движении численно равна работе, которую необходимо совершить с тем, чтобы разогнать тело из состояния покоя до некоторой скорости.

Как видим, определением кинетической энергии W_K является не формула, а «рецепт» её нахождения. Выведем формулу для W_K, воспользовавшись определением.

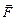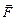Приложим к покоящемуся телу массой m постоянную силу ; будем считать, что других сил нет. Тело начнёт двигаться по прямой (направление действия силы не меняется), и в итоге совершит перемещение (при таком движении, очевидно, угол между векторами и равен нулю) и в итоге приобретёт скорость u. С учётом формулы второго закона Ньютона совершаемая силой работа записывается в виде

A = = = = = .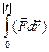

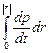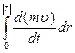Если масса тела не меняется в процессе движения, m можно вынести за знак интеграла, и тогда (с учётом того, что первая производная от перемещения по времени называется скоростью), получим:

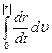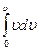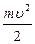A = m = m = , или

W_K = 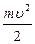. (4.8)

При обсуждении второго закона Ньютона мы уже отмечали, что масса реальных объектов со временем меняется (расходуется горючее, истираются детали и т. д.). При достижении больших скоростей станет заметным увеличение массы тела (см. далее раздел «специальная теория относительности»). Во всех этих случаях, согласно определению, приобретённая телом кинетическая энергия будет равна работе, совершаемой по разгону тела до скорости u, однако формула для её расчёта окажется иной, и её вид будет зависеть от закона, по которому масса тела менялась со временем.

Заметим: можно показать, что кинетическая энергия твёрдого тела, вращающегося вокруг неподвижной оси с угловой скоростью w численно равна работе, которую необходимо совершить с тем, чтобы раскрутить это тело из состояния покоя до данной скорости и выражается формулой

W_K = 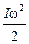. (4.9)

Здесь I – момент инерции тела относительно оси вращения.

Если же тело массой m одновременно совершает поступательное движение в некоторой плоскости и при этом вращается с угловой скоростью w относительно оси, проходящей через центр масс тела и сохраняющей свою ориентацию в пространстве, его общая кинетическая энергия рассчитывается по формуле

W_K = + 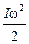. (4.10)

Здесь u_C – скорость центра масс тела, I – момент инерции тела относительно оси вращения.

4.2.3 Первая и вторая космические скорости

Рассмотрим пример расчёта работы переменной силы в случае, когда этой сила является результатом гравитационного взаимодействия двух тел. Рассчитаем величину второй космической скорости u_2К – такой минимальной скорости, которую необходимо придать телу на поверхности планеты с тем, чтобы после «броска» оно смогло улететь бесконечно далеко (притяжением других планет, звёзд пренебрегаем).

Из школьной программы мы помним, что первой космической называется минимальная скорость u_1К, которую необходимо сообщит телу с тем, чтобы после броска оно не упало на поверхность планеты, а двигалось над этой поверхностью по круговой орбите. При таком движении радиус траектории практически равен радиусу планеты R (которую считаем однородным шаром), а центростремительное ускорение a_Ц создаётся силой гравитационного притяжения F (M – масса планеты, m – масса тела), рис. 4.3:

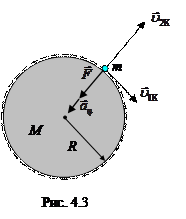
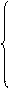F = ma_ц,

F = G º mg,

a_ц = .

Отсюда получаем: u_1К = 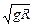, что для Земли составляет примерно 7,8 км/с.

Для расчёта второй космической скорости необходимо вычислить работу, которая совершается силой притяжения при перемещении тела с поверхности планеты на бесконечно большое расстояние и учесть, что вся эта работа пойдёт на уменьшение кинетической энергии тела. У поверхности планеты эта энергия должна равняться

W_K1 = 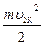, а на бесконечности W_K2 = 0 (тело останавливается, но не падает обратно), то есть W_K2 - W_K1 = - .

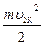Итак, работа силы притяжения:

A = = = - = - = - .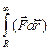

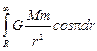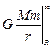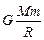Теперь учтём, что A = W_K2 - W_K1, и что = g. Получим:

u_2К = = u_1К. (4.11)

Для Земли u_2К » 11,2 км/с.

Формула для второй космической скорости выводилась в предположении, что на улетающее от Земли тело не действуют никакие объекты, кроме нашей планеты. На деле это не так: для того, чтобы улететь на бесконечно далёкое расстояние следует преодолеть силу притяжения самого массивного объекта Солнечной системы: Солнца. Минимальная скорость, необходимая для этого, называется третьей космической, она составляет примерно 16 км/с. Современные ракетные двигатели пока не способны придать космическому кораблю такую скорость. Поэтому для того, чтобы искусственные аппараты типа «Pioneer» и «Voyager» всё же смогли покинуть пределы Солнечной системы, траектории их полёта выбирались таким образом, чтобы аппараты пролетали мимо планет-гигантов (Юпитера, Сатурна, Урана), которые своими гравитационными полями помогали им преодолеть силу притяжения Солнца.

4.2.4 Потенциальная энергия (определения)

Если в каждой точке пространства на тело действует некоторая вполне определённая сила, то говорят, что тело находится в поле сил (будем считать далее, что величина и направление таких сил в каждой точке пространства не меняются со временем).

При перемещении тела из одной точки поля в другую силы этого поля (как любые силы, действующие на тело) могут совершать некоторую работу, рассчитать которую можно по формуле (4.2). Силы, работа которых не зависит от формы траектории, по которой перемещается тело, а определяется лишь его начальным и конечным положениями, называются консервативными. Примерами консервативных сил являются сила тяжести, сила электростатического взаимодействии, силы, возникающие при упругом деформировании тела.

Для поля консервативных сил можно ввести понятие потенциальной энергии W_П, величина которой, вообще говоря, в разных точках поля может быть различна (более того, в полях разной природы и формулы для расчёта этой энергии оказываются неодинаковыми)! Но во всех случаях справедливо определение: убыль[4] потенциальной энергиипри перемещении тела равна работе консервативных сил поля, совершённой при этом перемещении:

W_П1 - W_П2 = A. (4.12)

Принимая потенциальную энергию в какой-то точке поля равной нулю (например, W_П поля сил тяжести на поверхности Земли), можно вывести формулу для потенциальной энергии тела на любой высоте.

Некоторые примеры

- Земля не является идеальным шаром: она «сплюснута» у полюсов и «раздута» у экватора. Гравитационное воздействие Солнца и Луны на экваториальное «вздутие» приводит к возникновению моментов сил, вызывающих прецессию земной оси, которая описывает полный конус примерно за 26000 лет.

- Работа сердца взрослого человека за одно сокращение – примерно 1 Дж; за сутки – примерно 85 кДж.

- Мощность, развиваемая человеком при разовом движении – примерно до 3,5 кВт, при непрерывной интенсивной работе в течение 5 мин – до 1,5 кВт.

- Мощность двигателя автомобиля Chevrolet Niva с мотором «Опель-1,8»– 125 л. с. (или 92 кВт, так как 1 л. с. = 735,5 Вт, где л. с. – «лошадиная сила» – внесистемная единица измерения мощности;).

- Мощность паровоза «Ракета» Дж. Стефенсона – 13 л. с. (примерно 9,6 кВт).

- Мощность современного серийного тепловоза – более 8000 л.с. (5,9 МВт).

- Мощность современного серийного электровоза – более 10000 л.с. (7,4 МВт).

- Примерная мощность, развиваемая при экстренном торможении состава, двигавшегося со скоростью 200 км/ч – 10 МВт

- Суммарная мощность двигателей ракеты-носителя «Протон» – более 4,4×10⁷ кВт; ракеты-носителя «Энергия» – 1,25×10⁸ кВт.

Вопросы для повторения

1. В чём заключается явление прецессии гироскопа? Объясните, из-за чего оно возникает.

2. Что называется работой силы? В каких единицах она измеряется? Как рассчитывается работа в случае переменной силы? Приведите пример расчёта.

3. Что называется средней мощностью? Что называется мгновенной мощностью? В каких единицах мощность измеряется в СИ?

4. Что называется кинетической энергией тела при поступательном движении? Выведите соответствующую формулу для тела, масса которого не меняется в процессе движения.

5. Что называется первой космической скоростью? Выведите формулу для расчёта этой скорости.

6. Что называется второй космической скоростью? Выведите формулу для расчёта этой скорости.

7. Какие силы называются консервативными? Приведите примеры.

8. Сравните выражения для работы, мощности и кинетической энергии при поступательном и вращательном движениях тела.

Какие единицы измерения (в том числе – внесистемные) работы (энергии) и мощности Вам известны?