Умножение в D-кодах

Для выполнения операции умножения в D-кодах необходимо выполнить n циклов по числу десятичных разрядов множителя. После каждого цикла выполняется сдвиг содержимого сумматора и регистра множителя на один десятичный разряд влево. После выполнения умножения производится округление результата путем добавления к младшей (дополнительной) тетраде кода цифры 5. Знак произведения определяется в результате анализа знаков сомножителей. Очевидно, в простейшем случае в каждом цикле множимое прибавляется столько раз, сколько единиц содержится в очередной цифре множителя. Однако такой метод умножения характеризуется большими вычислительными, а следовательно, временными зат­ратами.

Для ускорения выполнения операции умножения в D-кодах можно, например, представить каждую десятичную цифру множителя как совокупность сложений с удвоенным или учетверенным множимым. Тогда, например, вместо выполнения семи сложений при умножении на цифру 7 достаточно выполнить три сложения: 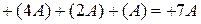, где A ­– множимое. Однако такой метод потребует дополнительных аппаратных ресурсов для хранения удвоенного и учетверенного множимых, так как процедура их получения предполагает помимо сдвига прибавление поправки к отдельным тетрадам, что исключает использование простых регистров.

Если при умножении на некоторые цифры множителя заменить операцию прибавления к содержимому сумматора на вычитание, то в некоторых случаях можно обойтись без учетверенного множимого либо уменьшить число операций на сумматоре. При этом, однако, может потребоваться корректировка отдельных цифр множителя.

Рассмотрим три варианта ускорения умножения (табл. 2.6). При использовании первых двух из них необходимо корректировать цифры множителя. Так, если очередная цифра множителя больше пяти, то последующая должна быть увеличена на единицу. Для хранения и модификации очередной цифры множителя в структуру устройства введем счетчик.

В качестве примера рассмотрим умножение двух чисел, представленных в D-коде 8421+3. В этом случае удвоение множимого выполняется следующим образом: множимое сдвигается на один двоичный разряд вправо, затем выполняется коррекция, которая заключается в прибавлении поправки 1101 к тем тетрадам, которые до сдвига содержали коды цифр
0–4, и поправки 0011 к тетрадам, содержавшим до сдвига коды цифр 5–9 (в случае D-кода 8421 коррекция делается путем прибавления поправки 0110 к тетрадам, содержавшим до сдвига коды цифр 5–9).

Таблица 2.6

Цифра множителя	Варианты выполнения операций на сумматоре

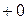
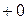
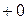
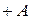
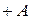
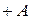
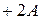
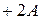
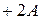
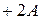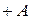
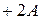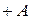
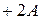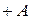
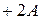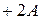
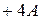
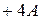
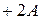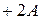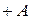
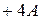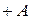
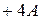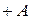
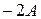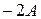
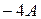
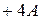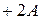
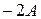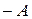
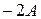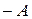
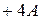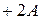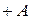
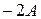
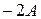
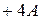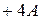
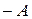
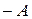
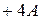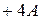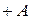
При выполнении умножения воспользуемся первым столбцом табл. 2.6. Для сохранения знака в сумматоре используем модифицированный код.

Пример.

; ;

.

;

;

.

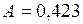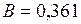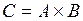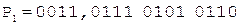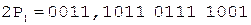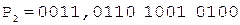При выполнении примера из соображений удобства и наглядности содержимое счетчика будем изображать десятичной цифрой.

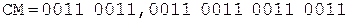
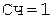
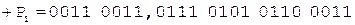
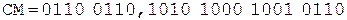
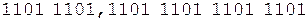Коррекция

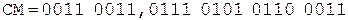
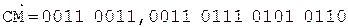
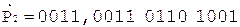
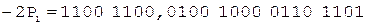
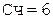
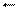
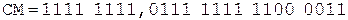
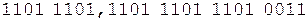Коррекция

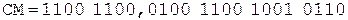
(окончание примера на следующей странице)

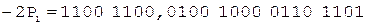
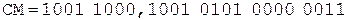
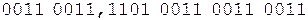Коррекция

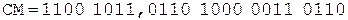
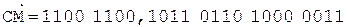
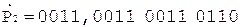
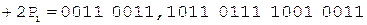
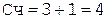
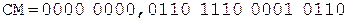
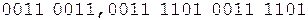Коррекция

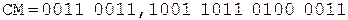
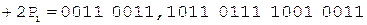
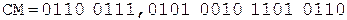
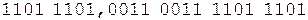Коррекция

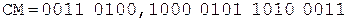
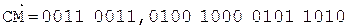
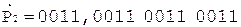
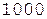Округление

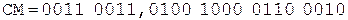
Таким образом, округляя до трех разрядов после запятой, получим .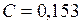

Действительно, 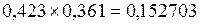, что после округления до исходных трех разрядов после запятой дает полученный выше результат.

Деление в D-кодах

По причине больших временных затрат алгоритм деления в D-кодах с восстановлением остатка обычно не реализуется в цифровых вычислительных устройствах, поэтому здесь будем рассматривать только алгоритм деления без восстановления остатка. В качестве упражнения читателю может быть предложено самостоятельно выполнить рассматриваемую арифметическую операцию с восстановлением и без восстановления остатка и оценить разницу в количестве выполняемых действий.

Рассмотрим следующую методику выполнения операции деления. Знак частного определяется в результате анализа знаков операндов по обычным правилам арифметики, после чего оба операнда делаются положительными. Чтобы исключить ситуацию с переполнением, будем рассматривать случай, когда модуль делимого меньше модуля делителя. Поскольку в рассматриваемом алгоритме делитель сдвигается вправо, для его хранения необходимо использовать регистр с k дополнительными двоичными разрядами; k определяется из неравенства 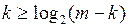, где m – число двоичных разрядов в представлении операндов. Очевидно, в сумматоре, содержащем делимое и частичные остатки, также должны быть предусмотрены k дополнительных разрядов. Учитывая особенности представления чисел в D-кодах, число дополнительных разрядов, определяемое вышеприведенным неравенством, при необходимости должно быть увеличено до образования соответствующего числа двоично-десятичных тетрад. Помимо сумматора и двух регистров (частного и делителя) устройство также должно содержать счетчик, используемый для формирования цифр частного.

Для получения n цифр частного необходимо выполнить n циклов деления. В первом такте каждого цикла содержимое регистра делителя сдвигается вправо на один десятичный разряд, а содержимое регистра частного сдвигается на один десятичный разряд влево. При этом в младший разряд регистра частного заносится текущее содержимое счетчика. Циклы делятся на четные и нечетные. Перед началом выполнения нечетных циклов в счетчике устанавливается цифра 0. Затем выполняется вычитание делителя до тех пор, пока содержимое сумматора не изменит знак на противоположный. В каждом такте вычитания (кроме последнего, соответствующего изменению знака) содержимое счетчика увеличивается на единицу. Перед началом выполнения четных циклов в счетчике устанавливается цифра 9. Затем выполняется прибавление делителя до тех пор, пока содержимое сумматора не изменит знак. В каждом такте сложения (кроме последнего) содержимое счетчика уменьшается на единицу. После выполнения n циклов необходимо выполнить действия, соответствующие первому такту 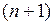-го цикла, для передачи последней определенной цифры частного из счетчика в соответствующий регистр.

Пример.

Операнды представим в D-коде 8421+3.

; ;

.

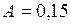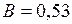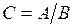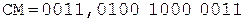
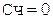
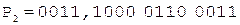
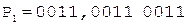
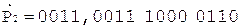
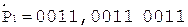
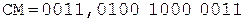
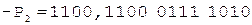
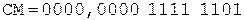
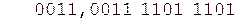Коррекция

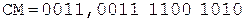
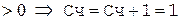
(окончание примера на следующей странице)

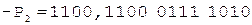
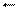
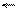
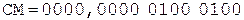
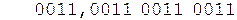Коррекция

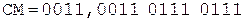
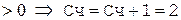
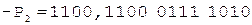
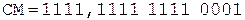
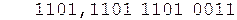Коррекция

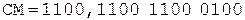
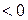
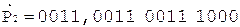
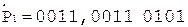
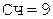
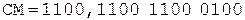
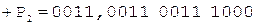
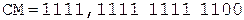
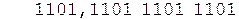Коррекция

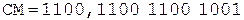
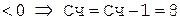
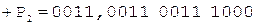
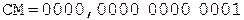
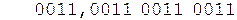Коррекция

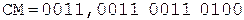
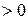
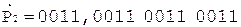
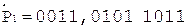
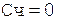
Таким образом, .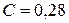

Вопросы для самоконтроля

1. В чем заключаются основные этапы выполнения операции сложения? Чем отличается выполнение операции вычитания?

2. В чем заключаются основные этапы выполнения операции умножения прямых кодов чисел? В чем различие методов умножения старшими и младшими разрядами вперед?

3. В чем заключаются основные этапы рассмотренных методов ускоренного выполнения операции умножения?

4. Чем отличается умножение инверсных кодов чисел от умножения прямых кодов?

5. В чем заключаются основные этапы выполнения операции деления прямых кодов чисел? В чем различие методов деления с восстановлением и без восстановления остатка?

6. В чем заключаются основные этапы рассмотренных методов ускоренного выполнения операции деления?

7. Чем отличается деление инверсных кодов чисел от деления прямых кодов?

8. В чем заключаются основные этапы выполнения операции извлечения квадратного корня? В чем различие методов с восстановлением и без восстановления остатка?

9. Особенности выполнения арифметических операций в D-кодах.