Умножение прямых кодов чисел
Рассмотрим сначала умножение младшими разрядами вперед. Для получения произведения необходимо выполнить n циклов умножения по числу разрядов сомножителей. При этом каждый цикл состоит из двух тактов. В первом такте анализируется младший разряд регистра, осуществляющего хранение множителя. Если в младшем разряде регистра множителя содержится единица, то к текущему содержимому сумматора следует прибавить содержимое регистра множимого, в противном случае к сумматору добавляется ноль, что эквивалентно пропуску такта сложения. Во втором такте каждого цикла умножения сумматор мантисс и регистр множителя следует сдвинуть вправо на один разряд. При этом сдвиг сумматора должен быть логическим, т.е. в освобождающийся знаковый разряд заносится 0. Это обстоятельство становится очевидным, если в сумматоре содержится модифицированный код, поскольку в случае переполнения сумматора в первом такте старший знаковый разряд остается неизменным и равным 0. В результате на сумматоре будет сформировано произведение исходных сомножителей.
После выполнения n циклов умножения необходимо выполнить округление результата путем прибавления к сумматору единицы в дополнительный 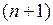 -й разряд. Далее результат нормализуется, если это необходимо, и ему присваивается знак.
-й разряд. Далее результат нормализуется, если это необходимо, и ему присваивается знак.
Пример.
[А]пр = 0,110001, [РА]пр = 1,011;
[В]пр = 1,100101, [РВ]пр = 0,101;
С = А ´ В.
Занесем операнды на регистры.
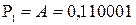 ;
; 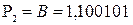 .
.
1. Определение знака произведения.
ЗнС = ЗнА Å ЗнВ = 0 Å 1 = 1.
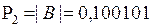 .
.
2. Определение порядка произведения.
РС = РА + РВ.
Выполним сложение порядков в модифицированном дополнительном коде.
|

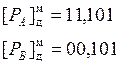
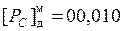
3. Умножение мантисс.

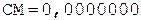
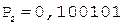
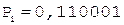
 1. +
1. + 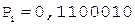
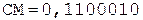
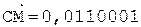
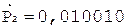
 2. +
2. + 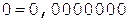
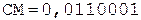
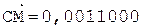
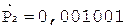
 3. +
3. + 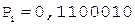
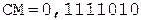
(окончание примера на следующей странице)

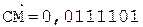
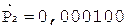
 4. +
4. + 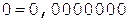
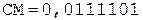
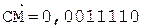
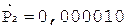
 5. +
5. + 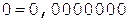
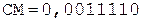
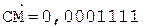
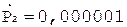
 6. +
6. + 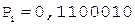
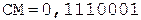
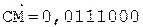
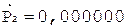
 Окр. +
Окр. + 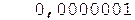
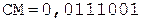
Отбросим дополнительный седьмой разряд и выполним проверку правильности умножения в десятичной системе счисления.
С = 0,011100(2) = 1/4 + 1/8 + 1/16 = 0,4375(10);
А´|В|= 0,110001(2) ´ 0,100101(2) = 0,765625(10) ´ 0,578125(10) » 0,4426(10).
Таким образом, погрешность составляет 0,0051, т.е. меньше половины веса шестого разряда.
4. Ограничение результата шестью разрядами, нормализация и присвоение знака.
Нормализация: 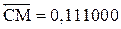 ;
; 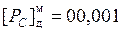 ;
;
Окончательно 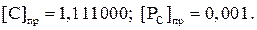
Как было сказано ранее, умножение можно выполнять не только младшими, но и старшими разрядами вперед. Для этого следует выполнить n циклов умножения по числу разрядов множителя. Каждый цикл распадается на два такта. В первом такте регистр множимого сдвигается на один разряд вправо, регистр множителя сдвигается на один разряд влево, сумматор в обоих тактах неподвижен. Во втором такте выполняется арифметическая операция сложения: если в знаковом разряде множителя содержится единица, то во втором такте к содержимому сумматора прибавляется множимое, в противном случае к сумматору прибавляется ноль. Такт суммирования очередного частичного произведения с нулем можно пропускать.
Следует помнить, что сумматор и регистр множимого должны иметь дополнительные разряды, так как в результате сдвига вправо множимое теряет значащие разряды. Количество дополнительных разрядов k должно удовлетворять следующему неравенству:
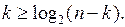
Все остальные этапы умножения такие же, как и в случае умножения младшими разрядами вперед.
Пример.
[А]пр = 0,110001, [РА]пр = 1,011;
[В]пр = 1,100101, [РВ]пр = 0,001;
С = А ´ В.
Занесем операнды на регистры, при этом для удобства учтем дополнительные разряды, число которых определяется подбором. Учитывая, что число основных разрядов 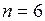 , достаточно будет ввести
, достаточно будет ввести 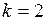 дополнительных разряда, поскольку
дополнительных разряда, поскольку 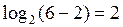 .
.
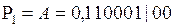 ;
; 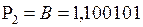 .
.
1. Определение знака произведения.
ЗнС = ЗнА Å ЗнВ = 0 Å 1 = 1.
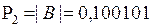 .
.
2. Определение порядка произведения.
РС = РА + РВ.
Выполним сложение порядков в модифицированном дополнительном коде.
|

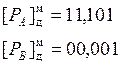
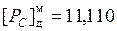
В прямом коде порядок произведения может быть записан как 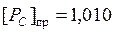 .
.
3. Умножение мантисс.
 1.
1. 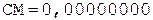
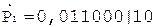
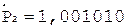

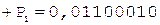
2. 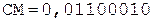
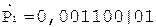
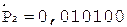
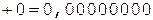
 3.
3. 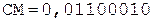
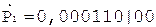
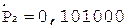
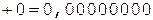
 4.
4. 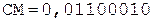
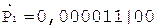
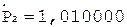
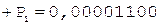
 5.
5. 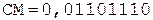
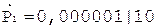
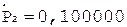
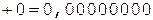
 6.
6. 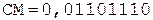
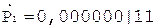
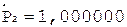

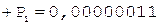
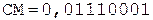
Окр. + 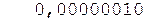

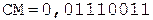
4. Ограничение результата шестью разрядами, нормализация и присвоение знака.
Нормализация: 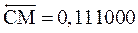 ;
; 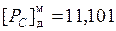 ;
;
Окончательно 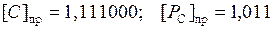 .
.
Дата добавления: 2020-02-05; просмотров: 820;











