Законы распределения времени между отказами

Время между соседними отказами является непрерывной случай­ной величиной. Эта случайная величина с вероятностной точки зре­ния будет полностью определена, если известна ее функция распре­деления. В теории надежности время между соседними отказами удобно характеризовать функцией распределения и ее производной – плотностью распре­деления. Это объясняется тем, что количественные характеристики надежности, а именно вероятность отказа и частота отказов, является соответственно функцией распределения и плотностью распре­деления времени между соседними отказами.

Принятый закон распределения является лишь математической моделью истинного закона распределения. Одной из основных задач теории надежности является выявление и математическое описание истинного закона распределения с возможно наибольшей степенью достоверности.

Случайные величины в зависимости от их физического смысла могут иметь различные законы распределения. В теории вероятностей известно большое число таких законов. Однако рассматривать коли­чественные характеристики надежности имеет смысл только для ограниченного их числа. Это объясняется тем, что на практике время между отказами сложных систем и простейших элементов подчиняется только определенным немногим законам распределения. При изучении надежности автоматизированных систем наиболее часто применяют законы распределения: экспоненциальный, нормальный, Вейбулла.

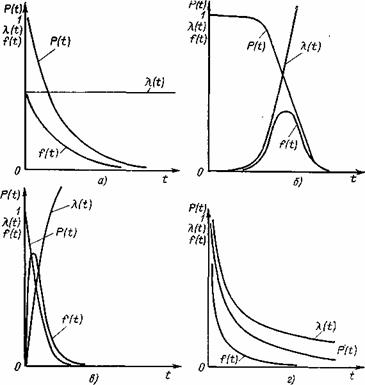
Наиболее распространенным законом распределения является экспоненциальный закон. При экспоненциальном законе распределения времени возникновения отказов интенсивность отказов является величиной постоянной. Тогда зависимости между основными количественными харак­теристиками надежности будут выражены формулами:

P(t) = e^-λt

f(t) = λe^-λt

λ(t) = λ = const

T_ср = 1/λ

где t – время работы изделия.

Графики основных количественных характеристик надежности для экспо­ненциального закона приведены на рис. а

Экспоненциальная модель может быть использована в случае, когда интенсивность отказов постоянная величина. Это условие реализуется приблизительно в период нормальной эксплуатации (график интенсивности), если исключить период приработки и период интенсивного старения. Экспоненциальное распределение хорошо описывает время безотказной работы сложных систем, состоя­щих из большого числа разнородных компонентов. Од­на из основных причин широкого использования экспоненциаль­ного закона заключается в том, что вследствие неизменности величины λ расчеты надежности при применении этого распре­деления наиболее просты.

Нормальный закон.В отличие от экспоненциального нормальное распределение используют для описания таких си­стем и их элементов, которые подвержены действию износа. При этом основные количественные характеристики будут выражены следующим образом:

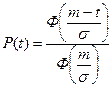
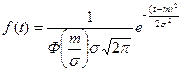
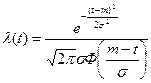
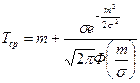
где Ф(x) – интеграл вероятностей или нормированная функция Лапласа; σ - среднеквадратическое отклонение времени безотказной работы; m – параметр нормального распределения.

Графики основных количественных характеристик надежности для нормального закона приведены на рис. б.

Усеченное нормальное распределение наблюдается при постепен­ных отказах электрических и механических элементов (график интенсивности) и широко ис­пользуется при анализе надежности сложных систем с учетом уходов параметров элементов за допустимые пределы.

Распределение Вейбулла. При распределении Вейбулла основные количественные характеристики рассчитываются по следующим формулам:

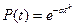
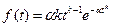
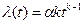
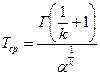
где k – параметр оп­ределяющий вид плотности распределения; α – параметр оп­ределяющий мас­штаб распределения; Г(x) – гамма-функция.

Это двухпараметрическое распределение. При k = 1 распределение Вейбулла сов­падает с экспоненциальным (рис. а), когда интенсивность отказов постоянна; при k > 1 интенсивность отказов монотонно возрастает (рис. в), при k < 1 монотонно убывает (рис. г).

Распределение Вейбулла может быть применено для описания наработки до отказа ряда электронных и меха­нических технических средств, включая период приработки.