Основные определения

Состояние системы. Неравновесное состояние системы характеризуется различными значениями ее параметров в каждой точке системы.

Равновесным считают такое состояние системы, при котором во всех ее точках параметры системы имеют одинаковые неизменные во времени значения.

Если все точки системы имеют одинаковую температуру, то считается, что система находится в состоянии термического равновесия. Если давление одинаково во всех точках системы ,то она находится в состоянии механического равновесия.

Опыт показывает , что система, выведенная из равновесия и не подвергающаяся больше внешним воздействиям, самостоятельно вернется в равновесное состояние. Из равновесного состояния в неравновесное система не может перейти без внешнего воздействия.

Если рабочее тело под воздействием внешних или внутренних факторов выведено из равновесия, то все параметры ,характеризующие его состояние, изменяются, т.е. начнется термодинамический процесс изменения состояния рабочего тела.

Термодинамический процесс может быть наглядно представлен в виде графика на pV – диаграмме :

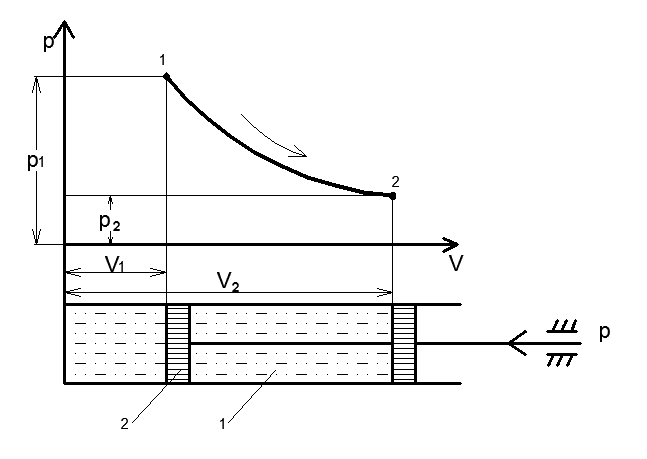
Рис 1.

Допустим, что в рабочем пространстве цилиндра 1 , снабженного поршнем 2 заключена масса газа m с начальными параметрами p₁ и υ₁ (точка 1). Примем, что на поршень с внешней стороны действует постоянная сила P и газ находится в состоянии равновесия.

Для осуществления процесса необходимо нарушить равновесие системы.

Процесс, переводящий тело из одного состояния в другое, из точки 1 в точку 2 , выразится некоторой кривой 1 -2 средних значений параметров. Точки1 и 2 точно характеризуют равновесное состояние газа в начале и в конце процесса. Вид кривой зависит от характера процесса . Такую кривую называют кривой термодинамического процесса.

Внутренняя энергия системы. Кинетическую энергию микроскопических тепловых движений молекул и потенциальную энергию их взаимодействия называют внутренней энергией тела.

В любом состоянии система, изолированная от внешней среды или находящаяся во взаимодействии с ней, имеет определенное количество внутренней энергии U.

Если состояние системы изменилось в результате любого термодинамического процесса, то изменение ее внутренней энергии не зависит от того, как протекал этот процесс, а зависит только от конечного и начального состояния рабочего тела. Поэтому такое изменение внутренней энергии тела в процессе определяется разностью значений энергии в начале и конце взаимодействия тела с внешней средой

s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t> </m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t> ,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000" wsp:rsidRPr="00891A89"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>">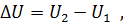

(17)

Где U₁ и U₂ – внутренняя энергии в начале и в конце процесса.

Работа и количество теплоты. Механическая работа, рас­сматриваемая в термодинамике, является мерой механической энергии. Она производится при перемещении тела в пространстве под действием механической силы.

Если газ, находящийся в цилиндре под поршнем, расширяется, то его объем увеличивается (d 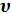>0). При этом газ передвигает поршень,

совершая механическую работу. Такую работу считают положи­тельной. При сжатии газа (d 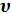<0) работа производится над газом со стороны внешней сре­ды. Эту работу считают отри­цательной.

Для того чтобы вычислить механическую работу, совер­шаемую термодинамической си­стемой, рассмотрим систему, представляющую собой т кг газа, находящегося в цилиндре, под поршнем (при р = const). Его состояние определяется па­раметрами р_1, V₁, Т_1, что на диаграмме (рис.1) соответ­ствует точке 1. Давление, газа p₁ уравновешено внешней силой Р, приложенной к штоку поршня . Таким образом, система находится в равновесии.

Подведем к системе теплоту Q, которая нарушит равновесное сос­тояние газа. Газ под действием теплоты, расширяясь, будет давить на поршень с силой R, преодолевая силу Р, и передвинет его вправо на расстояние х, совершив при этом работу. Состояние газа в точке определится параметрами р₂, V₂ и T₂.

Совершенную газом работу можно вычислить по общим правилам механики, а можно также определить графически, изобразив ее на pV-диаграмме.

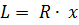
(18)

Как известно из механики, работа равна произведению силы на путь. В нашем случае работа L, совершенная газом под действием сил R, равна произведению этой силы на путь х:

Сила R, с которой газ передвигает поршень слева направо, равна произведению давления газа р на площадь поршня F:

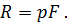
(19)

где

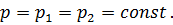
Подставив в формулу (18) значение R из формулы (19), получим

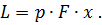
(20)

Но произведение площади F поршня на путь x представляет собой объем цилиндра между начальным и конечным положениями поршня:

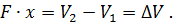
(21)

Подставив в формулу (20) значение объема цилиндра , получим величину работы, совершенной газом при его расширении:

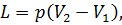
(22)

или

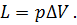
(23)

Из формулы видно, что изменение объема газа сопровождается ра­ботой, равной произведению давления, под которым находится газ, на изменение его объема.

Теперь по конечным параметрам газа построим график на pV- диаграмме, определяющий зависимость между его объемом в цилиндре и абсолютным давлением. Диаграмма дает возможность графически оценить работу расширения газа.(рис.2)

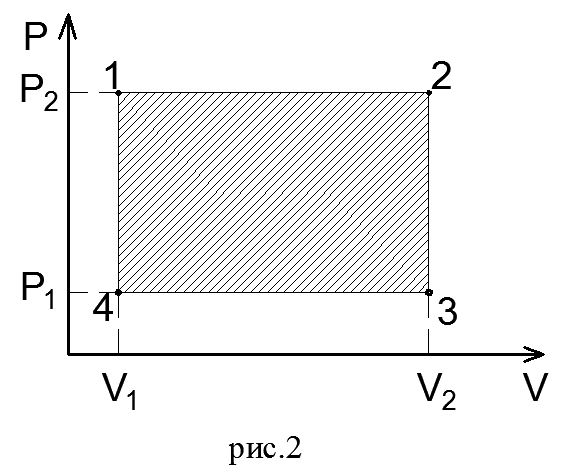
Так как давление газа в процессе рас­ширения принято постоянным, то линия процесса 1-2 на диаграмме параллельна оси абсцисс. Поэтому, опустив перпен­дикуляры из точек 1 и 2, начала и конца процесса, получим замкнутый контур в виде прямоугольника 12 3 4, образован­ный линией процесса 1-2, крайними ор­динатами 1,4 и 2,3 и отрезком оси абс­цисс, равным V₂— V₁. Площадь диаг­раммы, расположенная в этом контуре, на рV-диаграмме определяет работу расширения газа. Ее легко определить умножением ее основания на высоту.

В термодинамическом процессе, где давление меняется с измене­нием объема (рис.3), количество работы также определяется пл.1 2 3 4, ограниченной линией процесса 1-2, осью абсцисс 4,3 и край­ними ординатами 2,3 и 1,4. Однако замкнутый контур 1234 является сложной фигурой.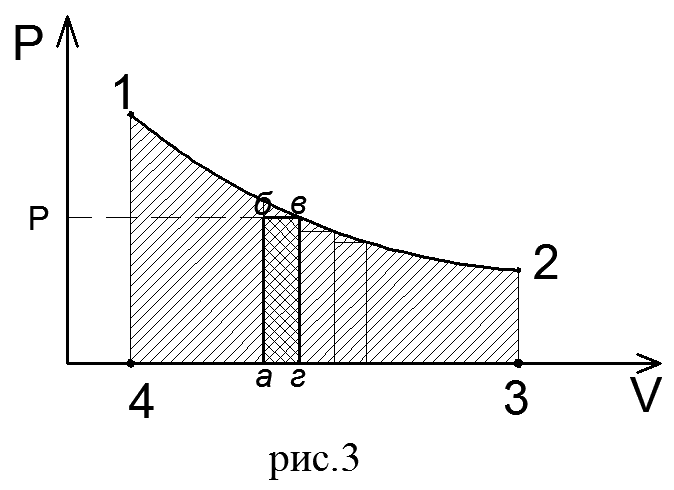

Эту работу можно вычислить аналитически. Для этого ра­зобьем весь процесс, изображенный на диаграмме кривой 1-2, на боль­шое число бесконечно малых процессов и определим работу расшире­ния газа одного такого элементарного процесса. В бесконечно малом изменении состояния газа изменение его параметров также бесконечно мало. Поэтому можно считать, что в пределах каждого элементарного процесса давление газа остается постоянным. Тогда по формуле (23) элементарная работа dL расширения газа при изменении объема на величину 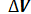= dV равна

d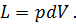

(24)

На рV-диаграмме элементарная работа dL изобразится в виде площади бесконечно узкого прямоугольника абвг (рис.3), величина которого определится произведением его основания на высоту р. Очевидно, кривая всего процесса 1-2 представится в виде ступенчатой кри­вой, составленной из элементарных процессов. Можно себе представить, что при бесконечном увеличении числа элементарных участков ступен­чатая кривая превратится в плавную кривую процесса.

Полная работа расширения т кг газа в процессе 1-2 определится суммой элементарных работ. Эта сумма равна определенному интегра­лу, взятому в пределах от начального объема V₁ до конечного объема V₂:

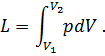
(25)

Отнеся работу расширения к 1 кг массы газа, получим

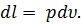
(26)

или

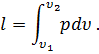
(27)

Количество теплоты в термодинамическом процессе является мерой тепловой энергии, подведенной к системе или отведенной от системы.

Не следует говорить о количестве теплоты, содержащейся в теле, а можно говорить лишь о том, сколько тело отдаст или получит теп­лоты в том или ином процессе. В отличие от внутренней энергии работа и количество теплоты зависят не только от начального и конечного состояния газа, но и от пути, по которому происходило изменение его состояния.

Количество теплоты, полученное телом, принято считать положи­тельным, а отданное телом — отрицательным.

Количества теплоты и работы измеряются в одних и тех же едини­цах— в джоулях (дж).

Закон сохранения энергии устанавливает, что энергия не создается, не уничтожается и что одна форма энергии может переходить в другую; при этом превращение совершается таким образом, что определенное количество одной формы энергии переходит в равное количество дру­гой формы энергии. Первый закон термодинамики по существу явля­ется законом сохранения энергии. Он устанавливает количественную зависимость между подводимой к системе теплотой, ее внутренней энергией и совершаемой системой работой (механической энергией).

Первый закон (начало) термодинамики формулируют так: вся теп­лота, подведенная к системе, расходуется на изменение внутренней энергии системы и на совершение внешней работы:

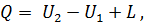
(28)

где Q — подведенная к системе теплота;

U₁— внутренняя энергия системы в начале процесса;

U₂— внутренняя энергия системы в конце процесса;

L — работа, совершенная системой.

Если первый закон выразить в дифференциальной форме и работу, совершенную газом, отнести к 1 кг газа, то уравнение (28) примет вид

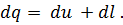
(29)

Первый закон термодинамики, устанавливая количественную зави­симость между видами энергии, не указывает условий, при которых протекают преобразования одного вида энергии в другой.

Сравнивая равенства (26) и (29), можно первый закон термоди­намики представить в виде

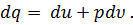
(30)

Следствие первого закона термодинамики

Применяя первый закон термодинамики возможно доказать, что теплоемкости одного и того же газа в процессах при постоянном давлении C_p и при постоянном объеме C_v различны по своей величине, а именно

Cp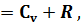

где R- газовая постоянная.

Для удобства термодинамических расчетов вводится новый параметр состояния рабочего тела—энтропия.

Рассмотрим уравнение первого закона термодинамики :

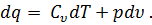
(31)

Разделив обе части этого уравнения на Т, получим

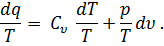
(32)

А так как из уравнения Клапейрона pv = RT следует, что

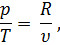
(33)

то подставив в равенство (32) значение р/Т из равенства (33), получим

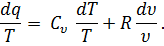
(34)

Правая часть этого уравнения представляет собой полный дифференциал некоторой функции переменных Т и V. Обозначив эту функцию через s, запишем

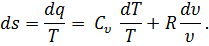
(35)

Другими словами, величина есть полный дифференциал ds функции s , определяемый состоянием газа (температурой и удельным объемом). Эту величину называют энтропией.

Уравнение (35) дает приращение энтропии при бесконечно малом изменении состояния газа. Проинтегрировав это уравнение, получим изменение энтропии для конечного изменения состояния 1 кг газа:

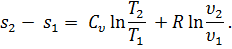
(36)

Энтропия так же, как и удельная теплоемкость, измеряется в 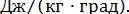Отсутствие приборов для измерения энтропии долгое время задерживало ее применение в решении технических задач. Простота и удобство применения энтропия в качестве параметра привели к широкому использованию ее в теплотехнических расчетах.

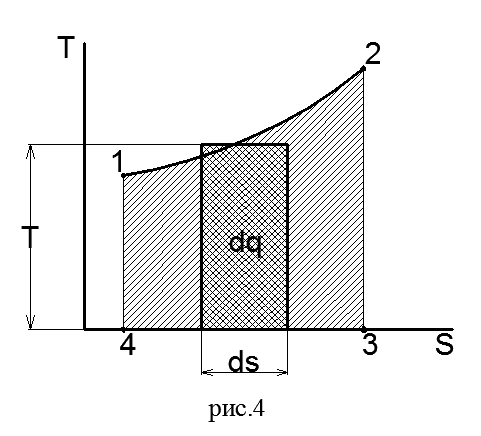Одним из важных вопросов теплотехники является подсчет теплоты, подведенной к двигателю и отведенной от него. По степени использования теплоты судят о работе двигателя и о его экономичности. Этот вопрос легко разрешается графическим изображением термодинамического процесса в системе координат, где по оси абсцисс откладывают значения энтропии, а по оси ординат - значения температуры. Так же, как и на pυ-диаграмме, состояния тела в каждый момент времени на Ts-диаграмме изображается точкой, процесс — линией. Теплота процесса на Ts-диаграмме определяется площадью под линией процесса.

Действительно, если линия 1-2 на Ts-диаграмме (рис.4) изображает произвольный процесс, то элементарное количество теплота процесса dq, равное Tds, численно равно площадке, имеющей высоту Т и основание ds. Вся теплота процесса численно равна пл. 12 3 4 под кривой процесса, так как

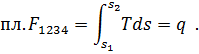
(37)

Если рυ-диаграмма дает возможность графически определить величину полученной (или затраченной) работы, то Тs - диаграмма позволяет судить о степени использования теплоты.

Рассмотрим уравнение (30) первого закона термодинамики:

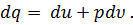
(38)

Напишем это уравнение для произвольного конечного процесса изменения состояния газа, определяемого участком любой кривой 1-2:

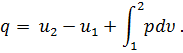
(39)

Так как

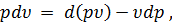
(40)

то уравнение (30) можно переписать:

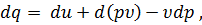
(41)

или

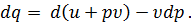
(42)

В первом члене правой части этого уравнения под знаком дифференциала стоит величина u + p 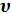. Эта величина складывается из внутренней энергии газа и и работы p 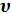, которую газ способен совершить при изменении своего объема от 0 до 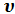при постоянном давлении р. Величину u + p 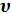называют энтальпией газа и обозначают буквой i:

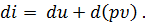
(43)

Энтальпия является одной из самых важных функций технической термодинамики.

Подставляя в уравнение первого закона термодинамики величину , найденную из уравнения (43), получим следующее выражение для первого закона термодинамики:

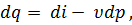
(44)

где 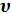dp — элементарная работа расширения газа с учетом его взаимо­действия с окружающей средой (с учетом работы проталки­вания).

Для процесса при р = const ( 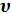dp = 0) уравнение (44) упрощается:

	(45)
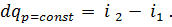
	(46)

Отсюда следует, что количество теплоты, которое передается в про­цессе с постоянным давлением, можно найти как разность энтальпий в конечном и начальном состояниях процесса р = const. При этом удобно использовать имеющиеся таблицы или диаграммы газов.