Плоская многослойная стенка
В практике большое значение имеет процесс передачи теплоты через плоскую стенку, состоящую из нескольких слоев материала с различной теплопроводностью. Так, например, металлическая стенка парового котла, покрытая с внешней стороны шлаками, а с внутренней накипью, представляет собой трехслойную стенку.
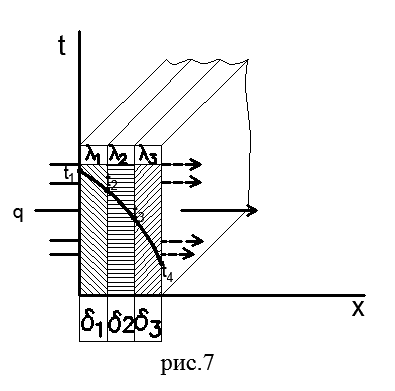 Рассмотрим процесс передачи теплоты теплопроводностью через плоскую-трехслойную стенку (рис.7). Все слои такой стенки плотно прилегают друг к другу. Толщины слоев обозначены δ1, δ2 и δ3, а коэффициенты теплопроводности каждого материала λ1, λ2 и λ3 соответственно. Известны также температуры наружных поверхностей tl и t4. Температуры t2 и t3 неизвестны.
Рассмотрим процесс передачи теплоты теплопроводностью через плоскую-трехслойную стенку (рис.7). Все слои такой стенки плотно прилегают друг к другу. Толщины слоев обозначены δ1, δ2 и δ3, а коэффициенты теплопроводности каждого материала λ1, λ2 и λ3 соответственно. Известны также температуры наружных поверхностей tl и t4. Температуры t2 и t3 неизвестны.
Процесс передачи теплоты теплопроводностью через многослойную стенку рассматривается при стационарном режиме, поэтому удельный тепловой поток q, проходящий через каждый слой стенки, по величине постоянен и для всех слоев одинаков, но на своем пути он преодолевает местное термическое сопротивление δ/λ каждого слоя стенки. Поэтому на основании формулы (54) для каждого слоя можно написать:
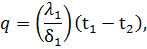
| |
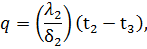
| |
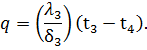
|
Из этих равенств можно определить изменение температуры в каждом слое:
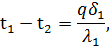
| |
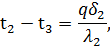
| (58) |
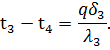
|
Складывая левые и правые части равенств (58), получим полный температурный напор, состоящий из суммы изменений температуры в каждом слое:
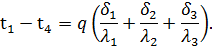
|
Из последнего соотношения можно определить величину удельного теплового потока q, проходящего через многослойную стенку:
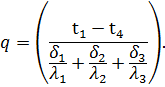
| (59) |
Из уравнения (59) следует, что общее термическое сопротивление многослойной стенки равно сумме термических сопротивлений каждого слоя:
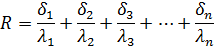
|
Для n-слойной стенки формула (13) примет вид
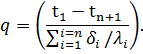
|
По формулам (58) и (59) можно получить значения неизвестных температур t2 и t3:
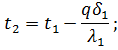
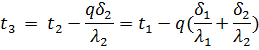
или
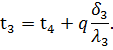
|
Распределение температуры в каждом слое стенки при λ-const подчиняется линейному закону, что видно из равенства (58). Для многослойной стенки в целом температурная кривая представляет собой ломаную линию (на рис.7).
Формулами, полученными для многослойной стенки, можно пользоваться при условии хорошего теплового контакта между слоями. Если между слоями появится хотя бы небольшой воздушный зазор, то термическое сопротивление заметно увеличится, так как теплопроводность воздуха очень мала:
[λВ03Д = 0,023 вт/(м 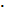 град)].
град)].
Если наличие такого слоя неизбежно, то при расчетах он рассматривается как один из слоев многослойной стенки.
Конвективный теплообмен. Конвективный теплообмен представляет собой теплообмен между твердым телом и жидкостью (или газом), сопровождающийся одновременно теплопроводностью и конвекцией.
Явление теплопроводности в жидкости, как и в твердом теле, полностью определяется свойствами самой жидкости, в частности коэффициентом теплопроводности и градиентом температуры.
При конвекции перенос теплоты неразрывно связан с переносом жидкости. Это усложняет процесс, так как перенос жидкости зависит от характера и природы возникновения ее движения, физических свойств жидкости, формы и размеров поверхностей твердого тела и т. д.
Рассмотрим случай протекания около твердой стенки жидкости, температура которой ниже (или выше) температуры стенки. Между жидкостью и стенкой происходит теплообмен. Переход теплоты от стенки к жидкости (или обратно) назовем теплоотдачей. Ньютон показал, что количество теплоты Q, которым обмениваются между собой в единицу времени стенка, имеющая температуру Тст , и жидкость, имеющая температуру Тж, прямо пропорционально разности температур Тст — Тж и площади поверхности соприкосновения S:
Q = αS (Тст — Тж) (60)
где α — коэффициент теплоотдачи, который показывает, каким количеством теплоты в течение одной секунды обмениваются жидкость и стенка, если разность температур между ними 1 К, а площадь поверхности, омываемой жидкостью, равна 1 м2. В СИ единицей коэффициента теплоотдачи является Вт/(м2 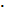 К). Коэффициент теплоотдачи α зависит от многих факторов, и в первую очередь от характера движения жидкости.
К). Коэффициент теплоотдачи α зависит от многих факторов, и в первую очередь от характера движения жидкости.
Турбулентному и ламинарному движению жидкости соответствует различный характер передачи теплоты. При ламинарном движении теплота распространяется в направлении, перпендикулярном перемещению частиц жидкости, так же как и в твердом теле, т. е. теплопроводностью. Так как коэффициент теплопроводности жидкости невелик, то распространяется теплота при ламинарном течении в направлении, перпендикулярном потоку, очень слабо. При турбулентном движении слои жидкости (более и менее нагретые) перемешиваются, и теплообмен между жидкостью и стенкой в данных условиях идет более интенсивно, чем при ламинарном течении. В пограничном слое жидкости (у стенок трубы) теплота передается только теплопроводностью. Поэтому пограничный слой представляет собой большое сопротивление потоку теплоты, и в нем происходит наибольшая потеря температурного напора.
Помимо характера движения, коэффициент теплоотдачи зависит от свойств жидкости и твердого тела, температуры жидкости и т. д. Таким образом, теоретически определить коэффициент теплоотдачи довольно сложно. На основании большого экспериментального материала найдены следующие значения коэффициентов теплоотдачи [в Вт/(м2 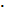 К)], для различных случаев конвективного теплообмена:
К)], для различных случаев конвективного теплообмена:
| Естественная конвекция газов | 5,8—34,7 |
| Движение газов в трубах или между ними | 11,6—116 |
| Движение водяного пара в трубах | 116—2 320 |
| Естественная конвекция воды | 116—1 160 |
| Движение воды по трубам | 575—11600 |
| Кипение воды | 2320—11600 |
| Конденсация пара | 4650—17500 |
В основном конвективный теплообмен происходит при продольном вынужденном течении жидкости, например теплообмен между стенками трубы и жидкостью, текущей по ней; поперечном вынужденном обтекании, например теплообмен при омывании жидкостью поперечного пучка труб; свободном движении, например теплообмен между жидкостью и вертикальной поверхностью, которую она омывает; изменении агрегатного состояния, например теплообмен между поверхностью и жидкостью, в результате которого жидкость закипает или происходит конденсация ее паров.
Лучистый теплообмен. Лучистым теплообменом называют процесс передачи теплоты от одного тела к другому в форме лучистой энергии. В теплотехнике в условиях высоких температур теплообмен излучением имеет первостепенное значение. Поэтому современные теплотехнические агрегаты, рассчитанные на высокие температуры, максимально используют этот вид теплообмена.
 Любое тело, температура которого отлична от абсолютного нуля, излучает электромагнитные волны. Их энергию способно поглотить, отразить, а также пропустить через себя какое-либо другое тело. В свою очередь, это тело также излучает энергию, которая вместе с отраженной и пропущенной энергией попадает на окружающие тела (в том числе и на первое тело) и вновь поглощается, отражается ими и т. д. Из всех электромагнитных лучей наибольшим тепловым действием обладают инфракрасные и видимые лучи с длиной волны 0,4—40 мкм. Эти лучи называют тепловыми.
Любое тело, температура которого отлична от абсолютного нуля, излучает электромагнитные волны. Их энергию способно поглотить, отразить, а также пропустить через себя какое-либо другое тело. В свою очередь, это тело также излучает энергию, которая вместе с отраженной и пропущенной энергией попадает на окружающие тела (в том числе и на первое тело) и вновь поглощается, отражается ими и т. д. Из всех электромагнитных лучей наибольшим тепловым действием обладают инфракрасные и видимые лучи с длиной волны 0,4—40 мкм. Эти лучи называют тепловыми.
В результате поглощения и излучения телами лучистой энергии происходит теплообмен между ними.
Количество теплоты, поглощаемое телом в результате лучистого теплообмена, равно разности между энергией, падающей на него, и излучаемой им. Такая разность отлична от нуля, если температура тел, участвующих во взаимном обмене лучистой энергией, различна. Если температура тел одинакова, то вся система находится в подвижном тепловом равновесии. Но и в этом случае тела по-прежнему излучают и поглощают лучистую энергию.
Энергию, излучаемую единицей поверхности тела в единицу времени, называют его излучательной способностью. Единица излучательной способности Вт/ма.
Если на тело в единицу времени падает Q0 энергии (рис.8), QR отражается, QD проходит через него, QA поглощается им, то
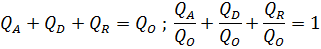
| (61) |
где QA/Q0 = A — поглощательная способность тела ; QR/Qo = R — отражательная способность тела; QD/Q0 = D — пропускающая способность тела.
Если А = 1, то R = D = 0, т. е. вся падающая энергия полностью поглощается. В этом случае говорят, что тело является абсолютно черным. Если R = 1,тоA=D = 0и угол падения лучей равен углу отражения. В этом случае тело абсолютно зеркально, а если отражение рассеянное (равномерное по всем направлениям) — абсолютно белое. Если D = 1,to A=R= 0 и тело абсолютно прозрачное. В природе нет ни абсолютно черных, ни абсолютно белых, ни абсолютно прозрачных тел. Реальные тела могут лишь в какой-то мере приблизиться к одному из таких видов тел.
Поглощательная способность различных тел различна; более того, одно и то же тело по-разному поглощает энергию различных длин волн. Однако есть тела, для которых в определенном интервале длин волн поглощательная способность мало зависит от длины волны. Такие тела принято называть серыми для данного интервала длин волн. Практика показывает, что применительно к интервалу длин волн, используемых в теплотехнике, очень многие тела можно считать серыми.
Энергия, излучаемая единицей поверхности абсолютно черного тела в единицу времени, пропорциональна четвертой степени абсолютной температуры (закон Стефана—Больцмана):
Е0 =σ'0ТА, где σ'0 — константа излучения абсолютно черного тела:
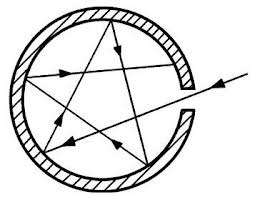
σ'0= 5,67-10-8 Вт/(м2- К4).
Часто этот закон записывают в виде
Рис.9. Модель абсолютно черного тела
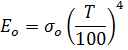
| (62) |
где 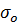 — коэффициент излучения абсолютно черного тела;
— коэффициент излучения абсолютно черного тела; 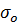 = 5,67 Вт/(м2
= 5,67 Вт/(м2  К4).
К4).
Многие законы излучения, установленные для абсолютно черного тела, имеют огромное значение для теплотехники. Так, полость топки котельной установки можно рассматривать как модель абсолютно черного тела (рис. 9). Применительно к такой модели законы излучения абсолютно черного тела выполняются с большой точностью. Однако пользоваться этими законами применительно к тепловым установкам следует осторожно. Например, для серого тела закон Стефана—Больцмана имеет вид, аналогичный формуле (62):
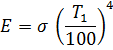
| (63) |
где 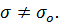 Отношение
Отношение 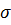 /
/ 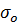 называют степенью черноты ε (ε тем больше, чем больше рассматриваемое тело отличается от абсолютного черного, табл. 4).
называют степенью черноты ε (ε тем больше, чем больше рассматриваемое тело отличается от абсолютного черного, табл. 4).
Формулу (63) используют для определения излучательной способности топок, поверхности слоя горящего топлива и т. п. Эту же формулу применяют при учете теплоты, переданной излучением в топочной камере, а также элементами котлоагрегата.
Тела, заполняющие внутреннее пространство топки, непрерывно излучают и поглощают энергию. Однако система этих тел не находится в состоянии теплового равновесия, так как их температура различна: в современных котлах температура труб, по которым проходят вода и пар, значительно ниже температуры топочного пространства и внутренней поверхности топки. При этих условиях излучательная способность труб значительно меньше
Таблица 4
| Материал | Температура, °С | ε | Материал | Температура, °С | ε |
| Алюминий шероховатый Вода | 20—50 0—100 | 0,06—0,07 0,95—0,96 0,88 -0,98 0,59 | Масляная краска Сталь окисленная | 200—600 | 0,95 0,74—0,80 |
| Кирпич красный | Уголь | 100— 600 | 0,81— 0,79 | ||
| » шамотный | Штукатурка | 10—90 | 0,91 |
излучательной способности топки и ее стенок. Поэтому теплообмен излучением, проходящий между ними, осуществляется главным образом в направлении передачи энергии от топки к поверхности труб.
При лучистом теплообмене между двумя параллельными поверхностями со степенями черноты ε3 и ε2, имеющими соответственно температуру T1 и Т2 количество энергии, которой они обмениваются, определяют по формуле
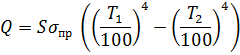
| (64) |
где S — площадь поверхностей; 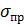 — так называемый приведенный коэффициент излучения, Вт/(м2
— так называемый приведенный коэффициент излучения, Вт/(м2  К4), для рассматриваемого случая:
К4), для рассматриваемого случая:
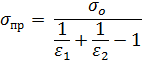
| (65) |
Если тела, между которыми происходит лучистый теплообмен, ограничены поверхностями и S1 и S2, расположенными внутри друг друга, то приведенный коэффициент излучения определяют по формуле
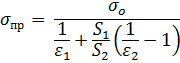
| (66) |
Теплопередача
Теплообмен между горячей и холодной средой через разделительную твёрдую стенку является одним из наиболее важных и часто используемых в технике процессов. Например, получение пара заданных параметров в котлоагрегатах основано на процессе передачи теплоты от одного теплоносителя к другому. В многочисленных теплообменных устройствах, применяемых в любой области промышленности, основным рабочим процессом является процесс теплообмена между теплоносителями. Такой теплообмен называют теплопередачей.
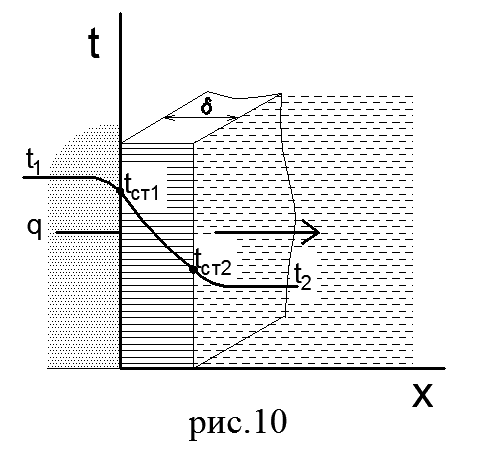
Для примера рассмотрим однослойную (рис.10) стенку, толщина которой равна δ. Коэффициент теплопроводности материала стенки равен λ. Температуры сред, омывающих стенку слева и справа, известны и равны t1 и t2. Примем, что t1>t2. Тогда температуры поверхностей стенки будут соответственно tст1> /tст2. Требуется определить тепловой поток q, проходящий через стенку от греющей среды к нагреваемой.
Так как рассматриваемый процесс теплопередачи протекает при стационарном режиме, то теплота, отданная стенке первым теплоносителем (горячим), передается через нее второму теплоносителю (холодному). Пользуясь формулой (54), можно записать:
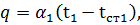
|
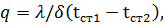
|
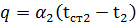
|
(67)
Определим полный температурный напор t1 – t2 . Для этого из равенств (67) определим сначала местные температурные напоры:
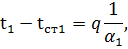
|
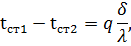
|
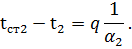
|
Складывая эти равенства, получим полный температурный напор:
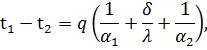
|
откуда определим - величину теплового потока:
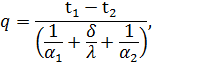
| (68) |
Знаменатель равенства (68) представляет собой сумму термических сопротивлений, которая, состоит из термического сопротивления теплопроводности δ/λ и двух термических сопротивлений теплоотдаче l/α1 и 1/α2.
Введем обозначение
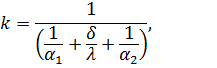
| (69) |
Из выражений (68) и (69) получим
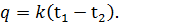
| (70) |
Величину k называют коэффициентом теплопередачи.
Величину, обратную коэффициенту теплопередачи, называют полным термическим сопротивлением теплопередаче:
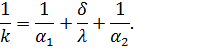
| (71) |
Дата добавления: 2016-06-15; просмотров: 10281;











