Ненасыщенные и насыщенные пары

Над свободной поверхностью жидкости всегда имеются пары этой жидкости, образующиеся за счет испарения. Если пространство над свободной поверхностью жидкости не ограничено какими – либо стенками, молекулы или атомы испарившегося вещества, совершая хаотическое тепловое движение, удаляется от поверхности жидкости. Удалению частиц пара от поверхности жидкости способствуют явление диффузии, а также естественная или искусственная конвекция слоев воздуха. Концентрация частиц пара при постоянной температуре в этих условиях может изменяться в широких пределах как в сторону уменьшения, так и в сторону увеличения. Такие пары называются ненасыщенными.

Иная картина наблюдается, если над свободной поверхностью жидкости имеется ограниченное пространство. Заполнено оно какими – либо другими газообразными веществами, кроме паров испаряющейся жидкости, или нет – значения не имеет. Важно заметить, что процесс испарения в замкнутое пространство может происходить только до определенного предела. Чем большей становится концентрация молекул или атомов испаряющегося вещества в парообразном состоянии, тем большим будет давление этих паров при постоянной температуре. При этом все большее число молекул или атомов может возвращаться через свободную поверхность обратно в жидкость. Если объем пространства , предоставленного парам, достаточно мал, а жидкости много, может наступить динамическое равновесие: число частиц, покидающих жидкость за единицу времени, уравняется с числом частиц, возвращающихся в жидкость за тот же промежуток времени. При этом над жидкостью будет находиться постоянная масса пара и большей концентрации его частиц в данных условиях достичь не удается. Такой пар называется насыщенным.

Давление насыщенного пара какого-то вещества при заданной температуре может иметь одно – единственное определенное значение.

Уменьшение объема пространства, предоставленного насыщенному пару данного вещества при постоянной температуре, приводит к конденсации части пара в жидкость, так как концентрация его частиц не может превысить определенного значения. Этим изотермическое сжатие насыщенных паров отличается от сжатия паров ненасыщенных, которые ведут себя как обычные идеальные газы. Закон Бойля – Мариотта , следовательно, для насыщенных паров не выполняется.

Закон Гей – Люссака также не применим к насыщенным парам, так как объем , предоставленный им, не зависит от температуры.

Неприменим к насыщенным парам и закон Шарля. При увеличении температуры идеальных газов или ненасыщенных паров в изохорическом процессе возрастает средняя кинетическая энергия их частиц, что приводит к их более частым соударениям между собой и со стенками сосуда, т.е. к повышению давления.

Говорить с уверенностью о том, что в данном закрытом сосуде содержится именно насыщенный пар какого-то вещества, можно только в том случае, если в сосуде имеется это вещество в жидком состоянии и масса его жидкой фазы не изменяется.

Например, перед нами поставили закрытый стеклянный сосуд и просят без всяких измерений определить, насыщенный или ненасыщенный водяной пар в нем содержится.

Для ответа на этот вопрос нужно подождать несколько минут, чтобы содержимое сосуда успело прийти в термодинамическое равновесие с окружающим воздухом. Это вызывается тем, что мы не знаем, из помещения с какой температурой принесен сосуд, а изменение температуры пара при неизменном объеме может привести пар из ненасыщенного состояния в насыщенное и обратно. Если после установления равновесия не обнаруживается конденсации воды на внутренних стенках сосуда, мы должны сказать, что при той температуре , при которой проводится наблюдение, в сосуде содержится ненасыщенны пар. Если же на стенках сосуда появляются капельки воды – пар насыщенный.

Пары воды в воздухе

В атмосфере Земли всегда содержаться водяные пары. С их присутствием приходится считаться очень часто. В особенности влажность воздуха подлежит точной оценке в закрытых или плохо вентилируемых помещениях, в сушильных камерах и т.д.

Для количественной оценки содержания водяных паров в воздухе используют две величины – абсолютную влажность (f) и относительную влажность (В).

Абсолютной влажностью называют физическую величину , измеряющуюся массой водяного пара, содержащегося в одном кубическом метре воздуха. Таким образом, абсолютная влажность совпадает с размерностью плотности, но на практике обычно пользуются единицей – 1г/м³ .

Последнее обстоятельство связано с тем, что абсолютная влажность f, выраженная в г/м³ , по численному значению мало отличается от парциального давления паров воды p при тех же условиях , измеренного в миллиметрах ртутного столба.

Процентное отношение парциального давления p паров воды, находящихся в воздухе, к давлению насыщенного пара воды p_н.п. при данной температуре называется относительной влажностью :

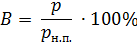
При расчете относительной влажности по этой формуле давление p и p_н.с. должны измеряться в одинаковых единицах. Обычно их измеряют не в паскалях, а в миллиметрах ртутного столба. Величину p_н.с определяют по таблицам.

Температура, при которой воздух в процессе своего охлаждения становится насыщенным водяными парами, называется точкой росы.

Лекция №2

ОСНОВЫ ТЕПЛОПЕРЕДАЧИ

Теплопередачей называют науку, изучающую закономерности процессов теплообмена между телами и распространения теплоты внутри одного тела. Изучение законов теплообмена необходимо для управле­ния тепловыми потоками, возникающими почти повсеместно в рабочих процессах машин, двигателей, аппаратов и т. п.

В теории теплопередачи рассматривается два основных вопроса:

I. Определение количества теплоты, которое передается от одного тела к другому или переходит из одной части тела к другой при за­данных условиях.

II. Определение температуры в разных участках тела, участвую­щего в процессе теплообмена.

Необходимым и достаточным условием теплообмена является раз­ность температур.

Теплота передается тремя способами: теплопроводностью, конвек­цией и излучением.

Теплопроводность— это процесс распространения тепловой энер­гии при непосредственном соприкосновении отдельных частей тела, имеющих различные температуры.

Конвекция — это процесс переноса энергии при перемещении объемов жидкости или газа в пространстве из области с одной температурой в область, имеющую другую температуру.

Излучение (лучистый теплообмен) — это процесс передачи энергии электромагнитными волнами. Теплопередача излучением представ­ляет собой двойное преобразование энергии: более нагретое тело излучает энергию в виде электромагнитных колебаний, другое менее нагретое тело поглощает энергию и нагревается.

Обычно теплообмен между телами совершается всеми тремя спо­собами одновременно. Сочетание их может быть самым разнообраз­ным. При этом один способ может преобладать над другим в зависи­мости от условий, в которых происходит теплообмен.

Однако при изучении процессов теплообмена следует четко раз­граничивать и отдельно рассматривать различные способы передачи теплоты (теплопроводность, конвекцию и излучение), поскольку они подчиняются различным законам.

Процессы теплообмена в теплотехнических устройствах могут протекать как при установившемся (стационарном), так и при неуста- новившемся (нестационарном) режимах. Стационарным (установив­шимся) тепловым режимом называют режим, при котором темпера­тура в любой точке тела не зависит от времени. Стационарному ре­жиму всегда предшествует нестационарный.

Процессы, протекающие в условиях нестационарного теплового режима (процессы нагрева и охлаждения), весьма сложны, и их рассмотрение не входит в программу данного курса. Поэтому здесь рассмотрены только стационарные процессы теплообмена.

ТЕПЛОПРОВОДНОСТЬ

Основные понятия

Теплопроводность — это молекулярный перенос теплоты в сплошной среде , обусловленный наличием разности температур.

Такой способ теплообмена имеет место в основном в твердых телах как внутри одного тела, так и между двумя телами при их соприкосно­вении друг с другом. Теплопроводность может осуществляться также и через слой жидкости или газа. Однако газы и жидкости, за исключе­нием расплавленных металлов, являются очень плохими проводни­ками теплоты.

Температурное поле. Процесс теплопроводности, так же как и другие виды теплообмена, осуществляется только при усло­вии, что в различных точках тела температура не одинакова. Как из­вестно, температура является параметром состояния тела и характе­ризует степень его нагретости. Совокупность значений температуры во всех точках рассматриваемого пространства в данный момент времени называют температурным полем. Математически температурное поле выражается функцией координат

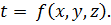
(47)

Температурное поле может быть функцией трех, двух и одной координаты. Если температура меняется в трех направлениях, то поле называют трехмерным.

Уравнения двумерного и одномерного полей имеют вид:

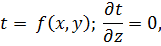
	(48)
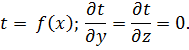
	(49)

Поверхность, во всех точках которой температура одинакова, называют изотермической.

Поскольку в одной и той же точке пространства одновременно не может быть двух различных температур, то разные изотермические поверхности никогда не пересекаются между собой. Все они либо оканчиваются на поверхности тела, либо целиком располагаются внутри него.

 

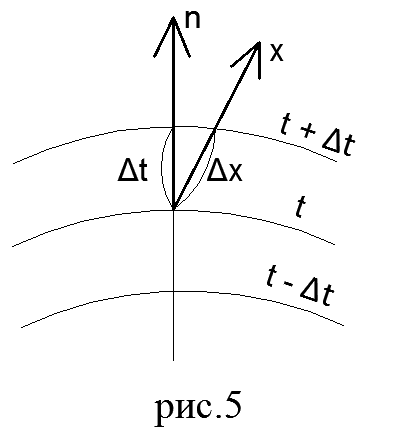Закон Фурье. Тепловым потоком называют количество теплоты Q, проходящее в единицу времени через произвольную поверхность. Вектор теп­лового потока всегда направлен в сторону уменьше­ния температуры.

Количественно интенсивность теплообмена харак­теризуется плотностью теплового потока q.

Плотностью теплового потока или удельным теп­ловым потоком, называют количество теплоты, про­ходящее через единицу поверхности F в единицу времени τ:

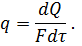
(50)

Так как теплота всегда передается от более нагретых частиц тела к менее нагретым, то вектор плотности теплового потока q всегда на­правлен в сторону уменьшения температуры.

Изучая процесс теплопроводности в твердых телах, французский ученый Фурье установил, что плотность теплового потока пропорцио­нальна градиенту температуры:

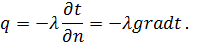
(51)

Соотношение (51) выражает основной закон теплопроводности и называется законом Фурье.

Знак минус в правой части соотношения (51) означает, что векторы теплового потока и градиента температуры направлены в противоположные стороны.

Коэффициент пропорциональности λ в выражении (51) есть фи­зический параметр вещества, называемый коэффициентом теплопро­водности. Он характеризует способность вещества проводить теплоту.

Размерность коэффициента теплопроводности определяется из выражения (51):

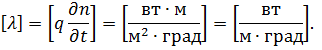
Следовательно, величина коэффициента теплопроводности числен­но равна удельному тепловому потоку через стенку единичной толщины при перепаде температуры 1^о С. Чем больше λ, тем лучшим провод­ником теплоты является вещество.

Хорошими проводниками теплоты являются металлы, плохим проводником теплоты — сухой неподвижный воздух. Легкие пористые материалы плохо проводят теплоту, так как их поры заполнены воз­духом. Материалы, коэффициент теплопроводности которых меньше 0,2 вт/(м-град), называют теплоизоляционными. Вода обладает плохой теплопроводностью, однако коэффициент теплопроводности влаж­ного материала резко увеличивается по сравнению с теплопровод­ностью его в сухом состоянии. Это объясняется тем, что вода в 20— 25 раз лучше проводит теплоту, чем воздух. Поэтому заполнение пор тела водой резко понижает его теплоизоляционные свойства.

Значение коэффициента теплопроводности λ для каждого тела находят экспериментально. Результаты сводят в таблицы, которыми пользуются при расчетах.

Теплопроводность стенки

Плоская однослойная стенка. На рис.6 показана плос­кая однослойная стенка толщиной δ из однородного материала (кир­пича, металла, дерева или любого другого).

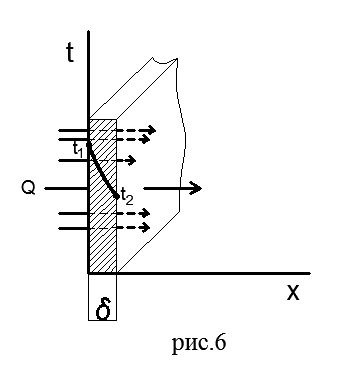Примем, что коэффициент теплопроводности материала λ не зависит от температуры. На наружных поверхно­стях стенки поддерживаются постоянные температуры t₁>t₂ ; температура изме­няется только в направлении оси х, пер­пендикулярной плоскости стенки, т. е. тем­пературное поле одномерно, а градиент температуры равен dt/dx.

Найдем плотность теплового потока, проходящего через заданную стенку, и установим характер изменения темпера­туры по толщине стенки.

Выделим внутри стенки элементарный слой толщиной dx, ограниченный двумя изотермическими поверхностями. Уравне­ние Фурье для этого слоя имеет вид

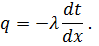
(52)

Разделив переменные, получим

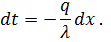
После интегрирования

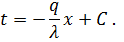
Постоянная интегрирования С определяется из граничных усло­вий: при x=0 t = t₁. Отсюда С =t₁ , следовательно, уравнение имеет вид

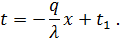
(53)

Из этого уравнения можно определить плотность теплового по­тока, проходящего через рассматриваемую стенку. Положив в урав­нении (53) х=δ, получим t= t₂, откуда

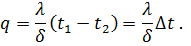
(54)

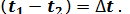Плотность теплового потока в плоской стенке прямо пропорцио­нальна коэффициенту теплопроводности λ, перепаду температур ( ) и обратно пропорциональна толщине стенки δ. Следует иметь в виду, что тепловой поток определяется не абсолютным значением температур, а их разностью — температурным напором Уравнение (54) является расчетной формулой теплопроводности плоской стенки. Оно связывает между собой четыре величины q, λ, δ и :

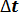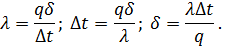
Зная любые три величины, можно всегда найти четвертую. Отно­шение λ/δ называют тепловой проводимостью стенки; она имеет раз­мерность [вт/(м² • град) ].

Если равенство (54) переписать в другом виде, то получим

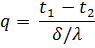
(55)

 

Отношение толщины стенки к коэффициенту теплопроводности δ/λ называют термическим сопротивлением стенки.

Из равенства (55) видно, что удельный тепловой поток прямо пропорционален перепаду температур и обратно пропорционален термическому сопротивлению стенки. Действительно, чем больше знаменатель дроби в уравнении (55), т. е. δ/λ, тем меньше плотность теплового потока q. Следовательно, с увеличением толщины стенки δ или с уменьшением теплопроводности λ уменьшается плотность теплового потока q.

Определив по формуле (54) плотность теплового потока, можно определить общее количество теплоты Q в джоулях, переданное через плоскую стенку поверхностью F за время τ:

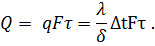
(56)

Если в формулу (53) подставить значение q из формулы (54), то можно получить уравнение температурной кривой:

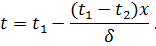
(57)

Это уравнение является уравнением прямой линии. Таким образом, при постоянном значении коэффициента теплопроводности темпера­тура по толщине однородной стенки изменяется линейно. В тех слу­чаях, когда коэффициент теплопроводности зависит от температуры, он является переменной величиной и расчет­ные формулы получаются несколько сложнее.