Лекция № 9. Ламинарное движение жидкости в круглой трубе. Формула Пуазейля.
Определим основные закономерности ламинарного режима при равномерном движении в круглых трубах, ограничиваясь случаями, когда ось трубы горизонтальна. При этом будем рассматривать уже сформировавшийся поток, т.е. поток на участке, начало которого находится от входного сечения трубы на расстоянии, обеспечивающим стабилизированный вид распределения скоростей по сечению потока.
Имея в виду сделанное раннее определение ламинарного режима, движения имеет слоистый (струйный) характер и происходит без перемешивания частиц, следует считать, что при этом будут иметь место только скорости, параллельные оси трубы, поперечные скорости отсутствуют. Можно представить себе, что в таком случае движущая жидкость как бы разделяется на бесконечно большое число бесконечно-тонких концентрично расположенных цилиндрических слоев, параллельных оси трубопровода и движущихся один внутри другого с различными скоростями, увеличивающимися в направлении от стенок оси трубы. При этом скорость в слое, непосредственно соприкасающемся со стенками, вследствие прилипания равна нулю, а максимального значения она достигает в слое, движущемся по оси трубы. Принятая схема движения и введенные выше упрощающие предположения позволяют установить закон распределения скоростей по поперечному сечению потока и получить расчетные зависимости для определения расхода жидкости и потери напора на трение по длине потока.
Будем исходить из установленного ранее общего выражения для градиента скорости, которое для течения в трубах нужно записывать следующим образом: 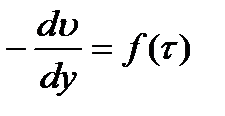 (1).
(1).
Знак минус здесь берется потому, что с увеличением у скорость υ убывает, т.е. 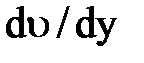 отрицательна, а напряжение τ- величина существенно положительная.
отрицательна, а напряжение τ- величина существенно положительная.
Примем затем, что имеет место прилипание жидкости к стенке (отсутствие скольжения) и поэтому скорость у стенки 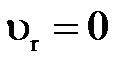 .
.
Тогда из выражения (1) будем иметь
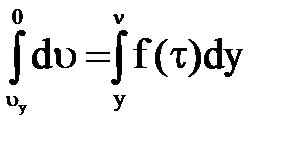 (2).
(2).
Учтем так же (это следует из закона распределения напряжений), что 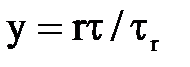 .
.
Найдем 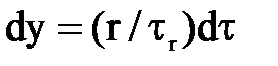 .
.
Сделав соответствующую подстановку в выражение (2) получим:
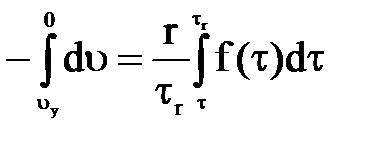 (3).
(3).
Следовательно 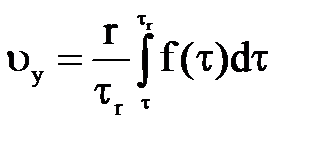
 (4).
(4).
Выражения (3) и (4) являются общими. Их интегрирование позволяет установить закон распределение скоростей при любом виде функции 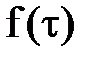 .
.
Решим эту задачу для течения в трубах ньютоновской жидкости. В этом случае 
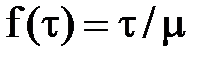 выражение (4) принимает вид
выражение (4) принимает вид
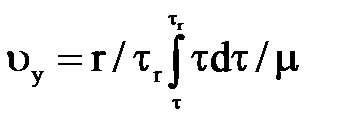
Интегрируя его находим 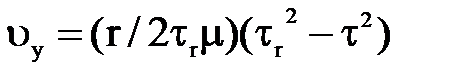 ,
,
что после ряда подстановок и несложных преобразований приводит к уравнению
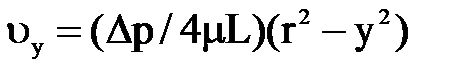 ,
,
выражающему закон распределения скоростей в поперечном сечении круглой трубы при ламинарном режиме, известный под названием закона Стокса. Его можно получить так же непосредственно интегрированием уравнений движения вязкой жидкости Навье- Стокса.
Задаваясь различными значениями координаты у, по этому уравнению можно вычислить скорости в любой точке сечения. Max скорость, очевидно будет при у=0, т.е. на оси трубы
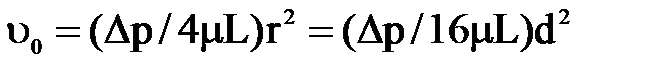
Попутно отметим, что средняя скорость потока при этом оказывается равной половине max осевой скорости; 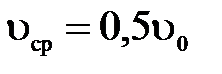 .
.
Изобразим уравнение закона Стокса графически. Для этого вычисленные значения скорости отложим в определенном масштабе от некоторой произвольной прямой АА в виде отрезков, направленных по течению жидкости и концы отрезков соединим плавной кривой. Полученная кривая представляет собой кривую распределения скоростей в поперечном сечении потока и, как это следует из закона Стокса, является параболой второй степени с осью, совпадающей с осью трубы.
Таким образом ,при ламинарном режиме в цилиндрической трубе скорости в поперечном сечении потока изменяются по параболическому закону, а касательные напряжения – по линейному закону.
Полученные результаты справедливы для участков трубы с вполне развившимся ламинарным течением. В действительности жидкость, которая поступает в трубу, должна пройти от входного сечения определенный участок, прежде чем в трубе установится соответствующий ламинарному режиму параболической закон распределения скоростей.
Развитие ламинарного режима в трубе можно представить следующим образом. Пусть, например, жидкость входит в трубку из резервуара большого размера и кромки входного отверстия хорошо закруглены. В этом случае скорости во всех точках входного поперечного сечения будут почти одинаковы, за исключением весьма тонкого так называемого пограничного (или пристенного) слоя в близи стенок, в котором в следствии прилипания жидкости к стенкам происходит почти внезапное падение скорости до нуля. Поэтому кривая скоростей во входном сечении может быть, представлена достаточно точно в виде отрезка прямой (а).
По мере удаления от входа слои жидкости, соседние с пограничным слоем, вследствие трения у стенок начинают затормаживаться, толщина этих слоев постепенно увеличивается, а движение в нем наоборот замедляется. Центральная же часть потока (ядро течения), еще не захваченная трением, продолжается двигаться как одно целое с примерно одинаковой для всех слоев скоростью, причем (вследствие того что количество протекающей жидкости остается неизменным) замедление движения в пограничном слое неизбежно вызывает увеличение скорости в ядре.
Таким образом, в середине трубы в ядре, скорость течения все время возрастает, а у стенок в растущем пограничном слое, уменьшается. Это происходит до сих пор, пока пограничный слой не захватит всего течения потока, и ядро не будет сведено к нулю. На этом формирование потока заканчивается, и кривая скоростей принимает обычную для ламинарного режима параболическую форму.
Входной участок трубы, на котором складывается постоянная параболическая картина распределения скоростей, носит название начального участка ламинарного режима.
Длина этого участка определяется по формуле:
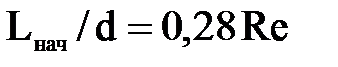 .
.
Дата добавления: 2016-06-15; просмотров: 2790;











