Примеры практического применения уравнения Д. Бернулли.

Уравнение Д.Бернулли является основным уравнением гидродинамики, с его помощью выводятся расчетные формулы для различных случаев движения жидкости и решается много практических задач.

Расходомер Вентури. Прибор для измерения расхода жидкости. Большим преимуществом этого прибора является простота конструкции и отсутствие каких-либо движущихся частей. Расходомеры Вентури могут быть расположены горизонтально, вертикально и под любым углом, что принципиального значения не имеет. Рассмотрим расходомер с горизонтальной осью.

Он состоит из двух цилиндрических труб А и В диаметром 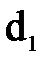, соединяемых посредством двух конических участков (патрубков) С и Д с цилиндрической вставкой Е меньшего диаметра 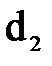. В сечениях 1-1 и 2-2 к расходомеру присоединены пьезометры а и в , которые показывают разность давлений в этих сечениях.

Составляя уравнение Бернулли для сечений 1-1 и 2-2 и пренебрегая очень небольшими на малой длине между этими сечениями потерями, получаем 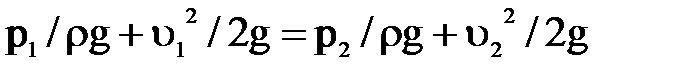, откуда

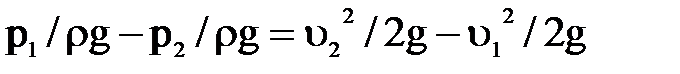
Но 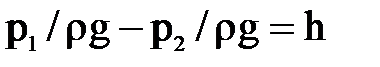и следовательно, .

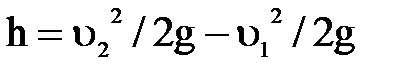Кроме того из уравнения постоянства расхода имеем .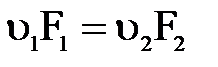

Выразим отсюда 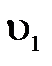через : .

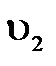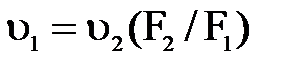Подставив это значение в предыдущее уравнение

,

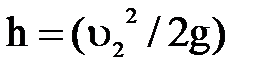
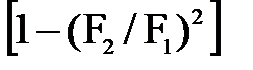определим среднюю скорость в сечении 2-2:

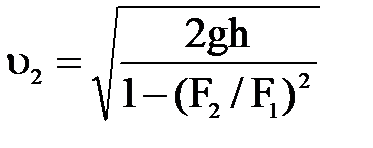
Тогда искомый расход жидкости будет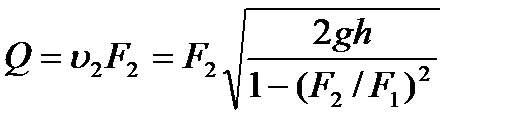

Однако вследствие неравномерности распределения скоростей в поперечных сечениях потока, а также неизбежных потерь напора между рассматриваемыми сечениями действительный расход жидкости будет несколько отличаться от вычисленного по этой формуле, что учитывают, вводя в нее поправочный коэффициент β.

В результате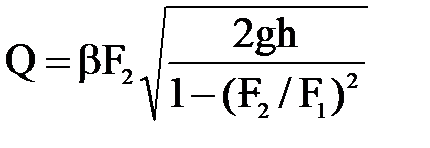

Коэффициент β для каждого расходомера устанавливают опытным путем на основании ряда предварительных измерений расходов при различных скоростях движения жидкости. В этом заключается градуирование расходомера.

Практически для определения расходомера пользуются формулой ,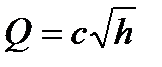

где коэффициент

Коэффициент С называют постоянной расходомера (для данного расходомера он имеет вполне определенное значение).

В большинстве случаев разность давлений в сечениях 1-1 и 2-2 трубчатого расходомера измеряют при помощи дифференциального манометра.

Трубка Пито.

Для замеров скорости в некоторой точке потока (как в небольших открытых потоках, главным образом, при лабораторных исследованиях, так и в трубах) применяют трубку Пито. В простейшим виде трубка Пито представляет собой изогнутую под прямым углом трубку небольшого диаметра, устанавливаемую в потоке открытым нижним концом навстречу течению жидкости; второй, верхний, конец трубки выводят из потока наружу.

Если такую трубку установить в открытом потоке, например в начале, где давление на свободной поверхности жидкости равно атмосферному, то как было указанно ранее, высота h поднятия жидкости в трубке над поверхностью потока представит собой величину скоростного напора 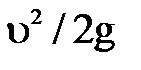в точке установки трубки.

Таким образом, 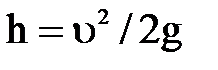, откуда скорость движения жидкости .

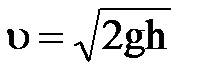Действительная скорость вследствие неизбежных потерь напора в самой трубке и некоторого нарушения потока, вызываемого введением в него инородного тела, оказывается несколько больше и определяется по формуле

,

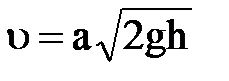где а-поправочный коэффициент, определяемый для каждой трубки опытным путем.

Дальнейшим развитием и усовершенствованием трубки Пито является устройство, применяемое для измерения скорости течения жидкости в напорных трубопроводах, состоящее из двух трубок, одна из которых а-обычный пьезометр, показывающий пьезометрический напор 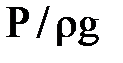, а другая b подобна трубке Пито и измеряет полный напор 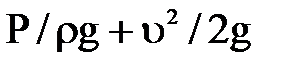. Разность уровней жидкости в обеих трубках h дает значение скоростного напора 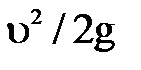, по которому определяют скорость.