Тема 3. Гидравлические сопротивления.
Лекция № 8. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса.
Одна из основных задач практической гидравлики- оценка потерь напора на преодоление гидравлических сопротивлений, возникающих при движение реальных жидкостей в различных гидравлических системах. Точный учет этих потерь во многом определяет надежность технических расчетов, степень совершенства и экономическую целесообразность инженерных решений, принимаемых при проектировании.
Чтобы правильно определить эти сопротивления, прежде всего необходимо составить представление о механизме самого движения жидкости. То что движение жидкости может происходить по разному, впервые отметил Г. Хаген (1869 г.)
Детальные экспериментальные исследования режимов движения жидкости выполнил английский физик О. Рейнольдс, результаты которых были опубликованы в 1883 г.
Конструкция и принцип действия прибора Рейнольдса следующие. Из резервуара В с исследуемой жидкостью и стеклянной горизонтальной трубы t, начало которой находится в резервуаре, а в конце ее имеется кран К для регулирования расхода. Расход измеряется с помощью мерного бака С. Вход из бака в трубу делается плавным для уменьшения возможных возмущений при поступлении жидкости в трубу
Над резервуаром В располагается маленький бачок Д, наполненный раствором краски той же плотности, что и вода. От бачка Д отходит тонкая трубка изогнутая внизу так, что ее заостренный, выходной конец вдвинут во входной участок стеклянной трубы t. Расход краски регулируется краном P.
Перед началом опыта жидкость в резервуаре выдерживается в покое в течении нескольких часов для устранения всех начальных возмущений .
При незначительном открытии крана из резервуара начинает вытекать жидкость через трубку t, в которой устанавливается средняя скорость, соответствующая данному расходу. Затем открывается кран К и Р внутри трубы движется тонкая окрашенная прямолинейная струйка, не смешиваясь со всей массой жидкости. При изменении положения тонкой трубки меняется и положение окрашенной струйки относительно стенок стеклянной трубы t, но раствор краски по прежнему будет двигаться отдельной струйкой. Следовательно, в стеклянной трубке жидкость движется отдельными струйками или слоями. Приоткрыв кран К побольше, то есть несколько увеличив скорость движения жидкости в трубе, можно наблюдать ту же картину раздельного течения исследуемой жидкости и раствора краски.
Однако после определенного открытия крана К струйка начинает приобретать волнообразное очертание- путь ее становится извилистым и неправильным, хотя струйка продолжает двигаться самостоятельно (υ).
При дальнейшим медленном открытии крана на отдельных участках струйки появляются разрывы и струйка теряет свою отчетливую форму.
Большее открытие крана К приводит к тому, что окрашенная струйка разрушается полностью и исчезает, а вся масса исследуемой жидкости в стеклянной трубе оказывается окрашенной, т.е. частицы жидкости при движении перемешиваются и движутся беспорядочно. Очевидно, что скорость движения исследуемой жидкости в трубе достигла некоторой критической величины, когда ее постепенные количественные изменения привели к качественным изменениям режима движения. Такую скорость называют верхней критической скоростью 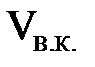 . Дальнейшее открытие крана К, и связанное с этим увеличение скорости в стеклянной трубке не приводит к внешнему изменению характера движения: вся масса движущейся жидкости будет оставаться окрашенной, увеличивается только степень беспорядочности движения частиц.
. Дальнейшее открытие крана К, и связанное с этим увеличение скорости в стеклянной трубке не приводит к внешнему изменению характера движения: вся масса движущейся жидкости будет оставаться окрашенной, увеличивается только степень беспорядочности движения частиц.
При обратном ходе опыта, то есть при постепенном закрытии крана, явление повторяется в обратном порядке, хотя переход от беспорядочного движения к струйному , упорядочному , происходит при более низких значениях критической скорости в трубе. Это скорость называется нижней критической скоростью 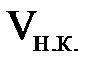 .
.
Режим движения, при котором имеет место слоистое движение жидкости, называется ламинарным (от латинского слова Lamina- слой), и в этом случае частицы жидкости не перемешиваются.
Беспорядочный режим движения, при котором происходит перемешивание частиц жидкости, называют турбулентным.
Следовательно, при скорости потока V меньше 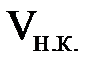
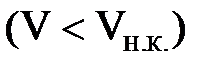 всегда будет ламинарный режим движения, а при
всегда будет ламинарный режим движения, а при 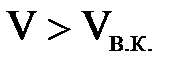 - турбулентный.
- турбулентный.
При скоростях в пределах 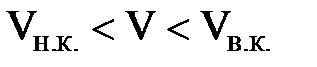 движения может быть и ламинарным и турбулентным. Оно зависит от изменения скорости движения жидкости. Если скорость уменьшается, то в зоне
движения может быть и ламинарным и турбулентным. Оно зависит от изменения скорости движения жидкости. Если скорость уменьшается, то в зоне 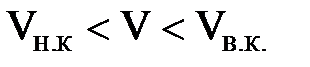 будет турбулентный режим движения, т.е. такой, которой был до этой зоны и наоборот, при увеличении скорости в этой зоне сохранится ламинарный режим движения.
будет турбулентный режим движения, т.е. такой, которой был до этой зоны и наоборот, при увеличении скорости в этой зоне сохранится ламинарный режим движения.
Значения 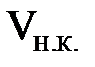 и
и 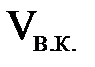 были установлены О. Рейнольдсом
были установлены О. Рейнольдсом
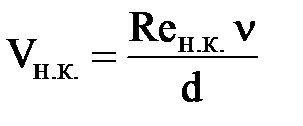 ;
; 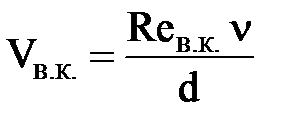 ,
,
где 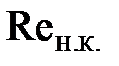 -нижнее критическое число Рейнольдса;
-нижнее критическое число Рейнольдса; 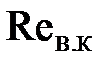 -верхнее критическое число Рейнольдса.
-верхнее критическое число Рейнольдса.
Критические числа Рейнольдса (названные двумя первыми буквами его фамилии)-безразмерные численные параметры, не зависящие от рода жидкости и размеров живого сечения потока. Опытами установлено что для трубопроводов нижнее критическое число Рейнольдса 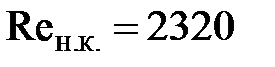 . Верхнее критическое число Рейнольдса
. Верхнее критическое число Рейнольдса 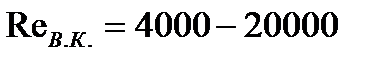 .
.
Изменяется в пределах от 4000 до 20000.
Вопрос о неустойчивости ламинарного режима и его переходе в турбулентный, а также о величине критического числа Рейнольдса подвергался тщательному теоретическому и экспериментальному изучению, но сих пор не получил еще достаточно полного решения.
Сопоставляя верхнее и нижнее критические числа, следует отметить, что они значительно отличаются друг от друга. Между ними имеется зона, в которой, как отмечено выше, в зависимости от условий может быть как ламинарный режим движения, так и турбулентный.
Как отмечает А.Д. Альтшуль, выполненные исследования показывают, что критическое число Рейнольдса увеличивается в сужающих трубах и уменьшается в расширяющихся. Это явление объясняется тем, что при ускорении движения в сужающихся трубах уменьшается тенденция частиц жидкости к поперечному перемешиванию, а в расширяющихся трубах при замедленном движении усиливается.
Так как в переходной зоне ламинированный режим неустойчив и легко переходит в турбулентный , то принимают одно расчетное критическое число Рейнольдса 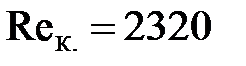 .
.
Для конкретных условий движения жидкости всегда можно установить действительное число Рейнольдса 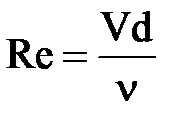 ,
,
где V- средняя в сечении скорость, определяемая при заданном расходе Q и размере трубопровода d: 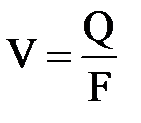 .
.
Затем полученное число Рейнольдса сравнивается с критическим и определяется режим движения: при 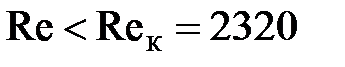 -режим движения ламинарный;
-режим движения ламинарный;
при 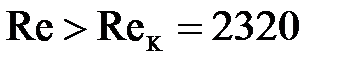 - режим движения турбулентный.
- режим движения турбулентный.
Для открытых русел, лотков, труб некруглого сечения или труб круглого сечения при безнапорном движении (то есть при неполном заполнении) число Рейнольдса, обычно выражается через гидравлический радиус R: 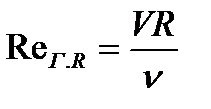 , в связи с тем, что
, в связи с тем, что
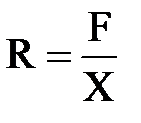 , а для труб
, а для труб 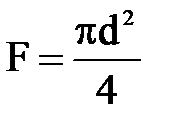 и
и 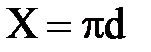 , то
, то 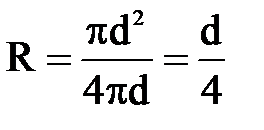 и,
и,
следовательно, соответствующее критическое число Рейнольдса 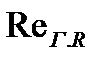 будет в 4 раза меньше
будет в 4 раза меньше 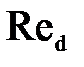 , то есть
, то есть 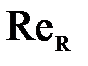 =580, обычно принято считать, что при
=580, обычно принято считать, что при 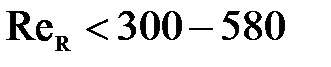 - движение ламинарное, а при
- движение ламинарное, а при 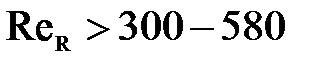 -турбулентное.
-турбулентное.
Ламинарный режим имеет место в тонких капиллярных трубках, при движении воды (фильтрации) в порах грунта, а так же при движении очень вязких жидкостей в трубопроводах (нефть, мазут, смазочное масло, сахарный сироп и др.)
В остальных случаях движения воды обычно наблюдается турбулентный режим движения.
Прибор Рейнольдса может быть использован для количественного определения потерь напора с помощью пьезометров.
Анализы данных опытов О. Рейнольдса и других исследователей показывают, что потери напора (энергии) 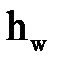 при ламинарном и турбулентном режиме движения резко различны.
при ламинарном и турбулентном режиме движения резко различны.
При ламинарном режиме движения потери напора пропорциональны средней скорости потока в первой степени: 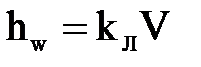 , где
, где 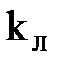 -коэффициент пропорциональности при ламинарном режиме.
-коэффициент пропорциональности при ламинарном режиме.
Для полностью развитого турбулентного режима движения в шероховатых водоводах потери напора пропорциональны средней скорости потока во второй степени (квадратичная область гидравлических сопротивлений)
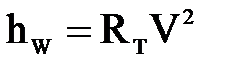 ,
,
где 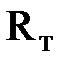 - коэффициент пропорциональности при турбулентном режиме.
- коэффициент пропорциональности при турбулентном режиме.
В переходной зоне 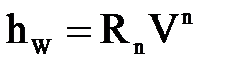 ,
,
где 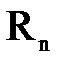 -коэффициент пропорциональности в переходной области, n- показатель степени;
-коэффициент пропорциональности в переходной области, n- показатель степени; 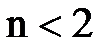 даже при полностью развитом турбулентном режиме движения в гладких водоводах (трубы).
даже при полностью развитом турбулентном режиме движения в гладких водоводах (трубы).
На рисунке графически показана зависимость потерь от скорости, которая наглядно показывает, что потери напора (энергии) определяются режимом движения жидкости: участок 1- ламинарный режим движения, участок 2- переходная зона неустойчивого режима движения, участок 3- турбулентный режим движения (квадратичный закон сопротивления).
Дата добавления: 2016-06-15; просмотров: 2444;











