Уравнение Бернулли для потока жидкости.

В гидравлике для характеристики удельной энергии часто используют понятие напора. Под напором понимают энергию жидкости, отнесенную к единице силы тяжести.

При решении различных практических вопросов о движении жидкостей приходится иметь дело не с элементарными струйками, а с потоками конечных размеров. Уравнение Бернулли в этом случае может быть получено при рассмотрении потока как совокупности множества элементарных струек.

Будем исходить из уравнения

,

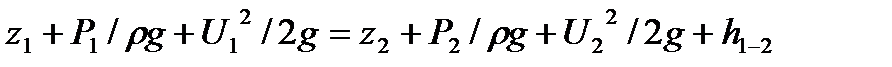где 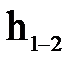- потеря энергии. Умножив все члены этого уравнения на 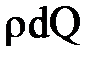(массовый расход жидкости), получим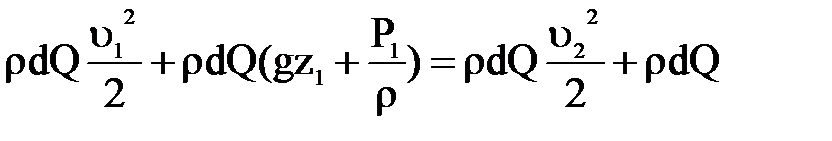

Подобные выражения можно составить для всех отдельных струек. Сложив их, будем иметь: 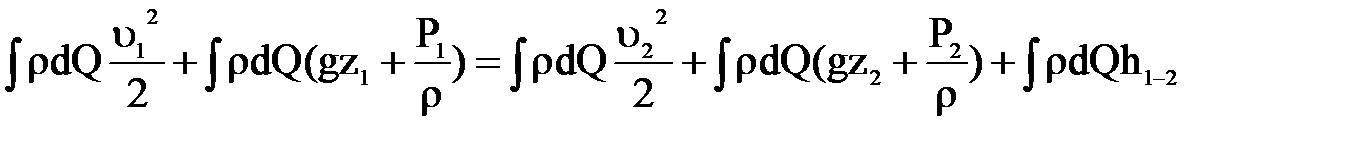(1)

Рассмотрим каждый из членов этого уравнения отдельно.

Выражения

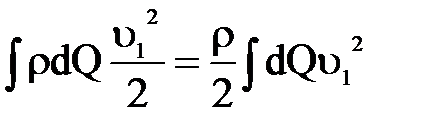и

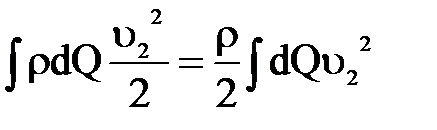
Представляют, значение кинетической энергии всей массы жидкости, протекающей в единицу времени через поперечные сечения потока 1-1 и 2-2. Для практических целей оказывается удобным эти выражения заменить выражениями кинетической энергии потока скорости 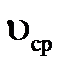, т.е. представить в виде

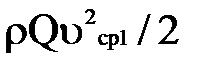и .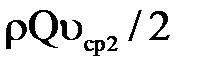

Однако .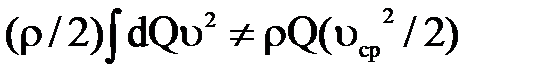

Объясняется это тем, что 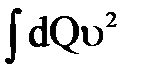есть арифметическая сумма произведений расходов отдельных элементарных струек (dQ) на квадраты их действительных скоростей 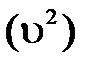, в то время как 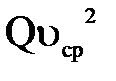-произведение суммарного расхода потока 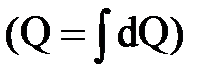на квадрат средней скорости потока 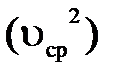, представляющий среднее арифметическое величин υ в первой степени ( 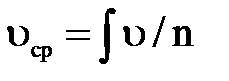, где n-число струек).

Поэтому, чтобы произведенная замена не изменила значение кинетической энергии потока, в выражение 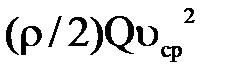необходимо ввести некоторый поправочный коэффициент α, называемый коэффициентом Корриолиса, этот коэффициент представляет собой отношение действительной кинетической энергии жидкости, протекающей через поперечное сечение потока в единицу времени, к кинетической энергии, которая имела бы место при том же расходе, если бы все частицы жидкости обладали одинаковыми скоростями, равными средней скорости, т.е. .

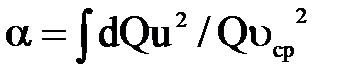С учетом того, что 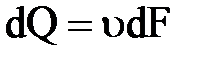и 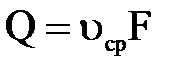, последнее выражение можно представить в виде .

Обычно коэффициент определяется опытным путем на основании изменений скорости в различных точках исследуемого потока. Он зависит от степени неравномерности распределения скоростей в его поперечном сечении и всегда больше единицы. Для ламинарного режима в цилиндрической трубе α=2, а для турбулентного α=1,045 1,10.

Рассмотрим теперь выражение второго члена уравнения (1), представляющего собой потенциальную энергию потока.

При медленном изменяющемся движении, которое в основном и рассматривается в гидравлике, распределение давлений в живых сечениях потока подчиняется основному закону гидростатики. Поэтому можно принять, что величина 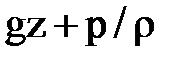во всех точках сечения такого потока будет одинакова и следовательно,

.

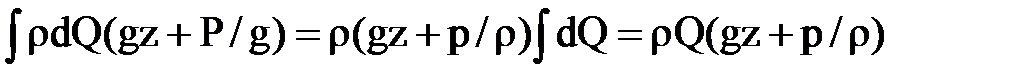Третий член уравнения (1), выражающий сумму работ сил сопротивления, можно представить (подразумевая под 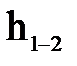осредненное значение потери удельной энергии) в виде .

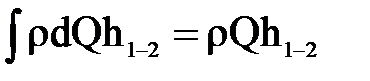Подставляя полученные выражения в уравнение (1), будем иметь:

.

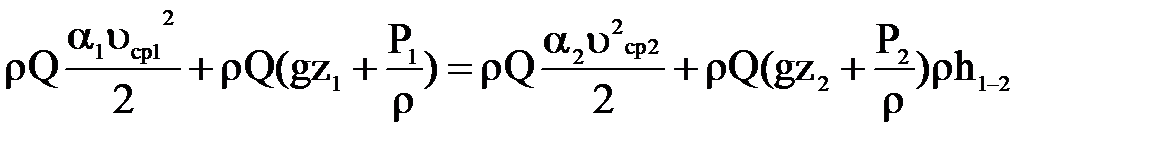Или после сокращения на 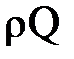и перегруппировки слагаемых

.

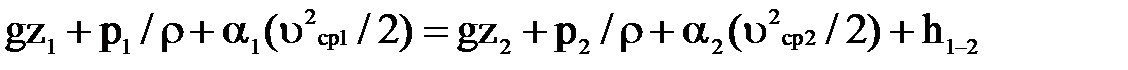Это и есть уравнение Бернулли для потока реальной жидкости.

При практических расчетах часто принимают α=1, тем самым пренебрегая неравномерностью распределения скоростей и полагая, что все струйки как бы движутся с одной и той же средней скоростью. Это и будет приниматься нами дальше (за исключением отдельных, особо оговариваемых случаев). Кроме того, мы будем опускать индексы «ср» при 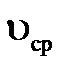, подразумевая везде, что речь идет о средних значениях этой величины. Тогда форма записи уравнения Бернулли для целого потока становится идентичной его записи для элементарной струйк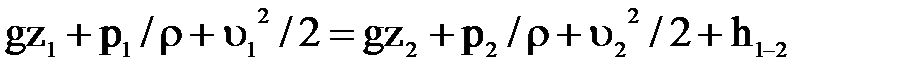и: или

.

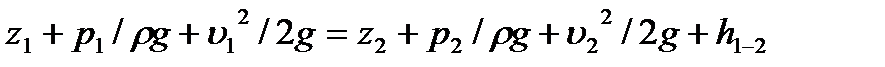В таком виде уравнение Бернулли обычно и применяют при решении практических задач для потоков однородной несжимаемой капельной жидкости при установившемся движении, происходящим под действием одной силы тяжести.